Обучение без учителя: Сжатие информации
....а мудрость его все возрастала, причиняя ему страдание полнотой своей. Ф. Ницше, " Так говорил Заратустра"
Обобщение данных. Прототипы задач
В этой лекции рассматривается новый тип обучения нейросетей - обучение без учителя (или для краткости - самообучение), когда сеть самостоятельно формирует свои выходы, адаптируясь к поступающим на ее входы сигналам. Как и прежде, такое обучение предполагает минимизацию некоторого целевого функционала. Задание такого функционала формирует цель, в соответствии с которой сеть осуществляет преобразование входной информации.
В отсутствие внешней цели, "учителем" сети могут служить лишь сами данные, т. е. имеющаяся в них информация, закономерности, отличающие входные данные от случайного шума. Лишь такая избыточность позволяет находить более компактное описание данных, что, согласно общему принципу, изложенному в предыдущей лекции, и является обобщением эмпирических данных. Сжатие данных, уменьшение степени их избыточности, использующее существующие в них закономерности, может существенно облегчить последующую работу с данными, выделяя действительно независимые признаки. Поэтому самообучающиеся сети чаще всего используются именно для предобработки "сырых" данных. Практически, адаптивные сети кодируют входную информацию наиболее компактным при заданных ограничениях кодом.
Длина описания данных пропорциональна, во-первых, разрядности данных  (т. е. числу бит), определяющей возможное разнообразие
принимаемых ими значений, и, во-вторых, размерности даных
(т. е. числу бит), определяющей возможное разнообразие
принимаемых ими значений, и, во-вторых, размерности даных  , т. е. числу компонент входных векторов
, т. е. числу компонент входных векторов 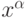 . Соответственно, можно различить
два предельных типа кодирования, использующих противоположные способы сжатия информации:
. Соответственно, можно различить
два предельных типа кодирования, использующих противоположные способы сжатия информации:
- Понижение размерности данных с минимальной потерей информации. (Сети, например, способны осуществлять анализ главных компонент данных, выделять наборы независимых признаков.)
- Уменьшение разнообразия данных за счет выделения конечного набора прототипов, и отнесения данных к одному из таких типов. (Кластеризация данных, квантование непрерывной входной информации.)
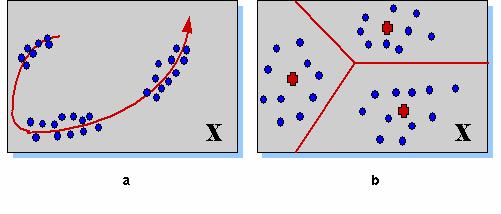
Рис. 4.1. Два типа сжатия информации. Понижение размерности (a) позволяет описывать данные меньшим числом компонент. Кластеризация или квантование (b) позволяет снизить разнообразие данных, уменьшая число бит, требуемых для описания данных
Возможно также объединение обоих типов кодирования. Например, очень богат приложениями метод топографических карт (или самоорганизующихся карт Кохонена - по имени предложившего их финского ученого), когда сами прототипы упорядочены в пространстве низкой размерности. Например, входные данные можно отобразить на упорядоченную двумерную сеть прототипов так, что появляется возможность визуализации многомерных данных.
Как и в случае с персептронами начать изучение нового типа обучения лучше с простейшей сети, состоящей из одного нейрона.
Нейрон - индикатор
Рассмотрим какие возможности по адаптивной обработке данных имеет единичный нейрон, и как можно сформулировать правила его обучения. В силу локальности нейросетевых алгоритмов, это базовое правило можно будет потом легко распространить и на сети из многих нейронов.
Постановка задачи
В простейшей постановке нейрон с одним выходом и d входами обучается на наборе d-мерных данных 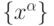 . В этой лекции мы сосредоточимся, в
основном, на обучении однослойных сетей, для которых нелинейность функции активации не принципиальна. Поэтому можно упростить
рассмотрение, ограничившись линейной функцией активации. Выход такого нейрона является линейной комбинацией его входов1Свободный член, как мы убедимся ниже, нам не потребуется.
. В этой лекции мы сосредоточимся, в
основном, на обучении однослойных сетей, для которых нелинейность функции активации не принципиальна. Поэтому можно упростить
рассмотрение, ограничившись линейной функцией активации. Выход такого нейрона является линейной комбинацией его входов1Свободный член, как мы убедимся ниже, нам не потребуется.
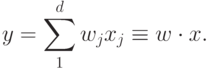
Амплитуда этого выхода после соответствующего обучения (т. е. выбора весов по набору примеров 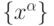 ) может служить индикатором того,
насколько данный вход соответствует обучающей выборке. Иными словами, нейрон может стать индикатором принадлежности входной информации
к заданной группе примеров.
) может служить индикатором того,
насколько данный вход соответствует обучающей выборке. Иными словами, нейрон может стать индикатором принадлежности входной информации
к заданной группе примеров.
Правило обучения Хебба
Правило обучения отдельного нейрона-индикатора по-необходимости локально, т. е. базируется только на информации непосредственно доступной самому нейрону - значениях его входов и выхода. Это правило, носящее имя канадского ученого Хебба, играет фундаментальную роль в нейрокомпьютинге, ибо содержит как в зародыше основные свойства самоорганизации нейронных сетей.
Согласно Хеббу (Hebb, 1949), изменение весов нейрона при предъявлении ему примера пропорционально его входам и выходу:
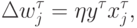
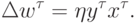
Если сформулировать обучение как задачу оптимизации, мы увидим, что обучающийся по Хеббу нейрон стремится увеличить амплитуду своего выхода:
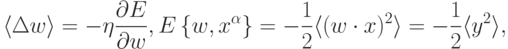
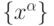 . Вспомним, что обучение с учителем, напротив, базировалось на идее уменьшения среднего
квадрата отклонения от эталона, чему соответствует знак минус в обучении по дельта-правилу. В отсутствие эталона минимизировать нечего:
минимизация амплитуды выхода привела бы лишь к уменьшению чувствительности выходов к значениям входов. Максимизация амплитуды, напротив,
делает нейрон как можно более чувствительным к различиям входной информации, т. е. превращает его в полезный индикатор.
. Вспомним, что обучение с учителем, напротив, базировалось на идее уменьшения среднего
квадрата отклонения от эталона, чему соответствует знак минус в обучении по дельта-правилу. В отсутствие эталона минимизировать нечего:
минимизация амплитуды выхода привела бы лишь к уменьшению чувствительности выходов к значениям входов. Максимизация амплитуды, напротив,
делает нейрон как можно более чувствительным к различиям входной информации, т. е. превращает его в полезный индикатор.Указанное различие в целях обучения носит принципиальный характер, т. к. минимум ошибки 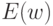 в данном случае отсутствует. Поэтому
обучение по Хеббу в том виде, в каком оно описано выше, на практике не применимо, т. к. приводит к неограниченному возрастанию амплитуды
весов.
в данном случае отсутствует. Поэтому
обучение по Хеббу в том виде, в каком оно описано выше, на практике не применимо, т. к. приводит к неограниченному возрастанию амплитуды
весов.
Правило обучения Ойа
От этого недостатка, однако, можно довольно просто избавиться, добавив член, препятствующий возрастанию весов. Так, правило обучения Ойа:
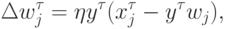
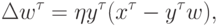
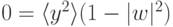 . Таким образом, веса обученного нейрона расположены на
гипер-сфере:
. Таким образом, веса обученного нейрона расположены на
гипер-сфере: 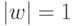 .
.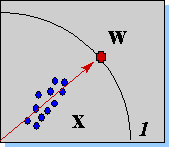
Рис. 4.3. При обучении по правилу Ойа, вектор весов нейрона располагается на гипер-сфере в направлении, максимизирующем проекцию входных векторов
Отметим, что это правило обучения по существу эквивалентно дельта-правилу, только обращенному назад - от входов к выходам
(т. е. при замене  ). Нейрон как бы старается воспроизвести значения своих входов по заданному выходу. Тем самым, такое обучение
стремится максимально повысить чувствительность единственного выхода-индикатора к многомерной входной информации, являя собой пример
оптимального сжатия информации.
). Нейрон как бы старается воспроизвести значения своих входов по заданному выходу. Тем самым, такое обучение
стремится максимально повысить чувствительность единственного выхода-индикатора к многомерной входной информации, являя собой пример
оптимального сжатия информации.
Эту же ситуацию можно описать и по-другому. Представим себе персептрон с одним (здесь - линейным) нейроном на скрытом слое, в котором число входов и выходов совпадает, причем веса с одинаковыми индексами в обоих слоях одинаковы. Будем учить этот персептрон воспроизводить в выходном слое значения своих выходов. При этом, дельта-правило обучения верхнего (а тем самым и нижнего) слоя примет вид правила Ойа:
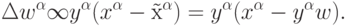
Таким образом, существует определенная параллель между самообучающимися сетями и т. н. автоассоциативными сетями, в которых учителем для выходов являются значения входов. Подобного рода нейросети с узким горлом также способны осуществлять сжатие информации.


