Предобработка данных
Отбор наиболее значимых входов
До сих пор мы старались лишь представить имеющуюся входную информацию наилучшим - наиболее информативным - образом. Однако, рассмотренные выше методы предобработки входов никак не учитывали зависимость выходов от этих входов. Между тем, наша задача как раз и состоит в выборе входных переменных, наиболее значимых для предсказаний. Для такого более содержательного отбора входов нам потребуются методы, позволяющие оценивать значимость входов.
Линейная значимость входов
Легче всего оценить значимость входов в линейной модели, предполагающей линейную зависимость выходов от входов:
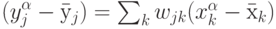
Матрицу весов  можно получить, например, обучением простейшего - однослойного персептрона с линейной функцией активации.
Допустим теперь, что при определении выходов мы опускаем одну, для определенности -
можно получить, например, обучением простейшего - однослойного персептрона с линейной функцией активации.
Допустим теперь, что при определении выходов мы опускаем одну, для определенности -  -ю компоненту входов, заменяя ее средним значением
этой переменной. Это приведет к огрублению модели, т.е. возрастании ошибки на величину:
-ю компоненту входов, заменяя ее средним значением
этой переменной. Это приведет к огрублению модели, т.е. возрастании ошибки на величину:
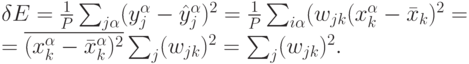
 -го входа определяется суммой квадратов соответствующих
ему весов.
-го входа определяется суммой квадратов соответствующих
ему весов.Особенно просто определить значимость выбеленных входов. Для этого достаточно просто вычислить взаимную корреляцию входов и выходов:
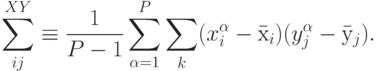
Действительно, при линейной зависимости между входами и выходами имеем:
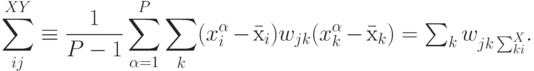
Таким образом, в общем случае для получения матрицы весов требуется решить систему линейных уравнений. Но для предварительно
выбеленных входов имеем: 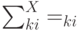 , так что в этом случае матрица кросс-корреляций просто совпадает с матрицей весов обученного линейного
персептрона:
, так что в этом случае матрица кросс-корреляций просто совпадает с матрицей весов обученного линейного
персептрона:  .
.
Резюмируя, значимость входов в предположении о приблизительно линейной зависимости между входными и выходными переменными для
выбеленных входов пропорциональна норме столбцов матрицы кросс-корреляций:  .
.
Не следует, однако, обольщаться существованием столь простого рецепта определения значимости входов. Линейная модель может быть легко построена и без привлечения нейросетей. Реальная сила нейроанализа как раз и состоит в возможности находить более сложные нелинейные зависимости. Более того, для облегчения собственно нелинейного анализа рекомендуется заранее освободиться от тривиальных линейных зависимостей - т.е. в качестве выходов при обучении подавать разность между выходными значениями и их линейным приближением. Это увеличит "разрешающую способность" нейросетевого моделирования (см. рисунок 7.12).
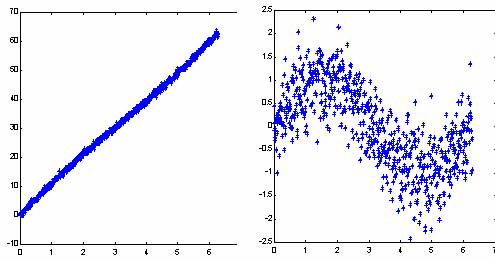
Рис. 7.12. Выявление нелинейной составляющей функции после вычитания линейной зависимости . ( Здесь - гауссовый случайный шум)
Для определения "нелинейной" значимости входов - после вычитания линейной составляющей, изложенный выше подход неприменим. Здесь надо привлекать более изощренные методики. К описанию одной из них, алгоритмам box-counting, мы и переходим.
Нелинейная значимость входов. Box-counting алгоритмы
Алгортимы box-counting, как следует из самого их названия, основаны на подсчете чисел заполнения примерами 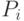 ячеек (boxes), на
которые специально для этого разбивается пространство переменных
ячеек (boxes), на
которые специально для этого разбивается пространство переменных  . Эти числа заполнения используются для оценки плотности вероятности
распределения примеров по ячейкам. Набор вероятностей
. Эти числа заполнения используются для оценки плотности вероятности
распределения примеров по ячейкам. Набор вероятностей 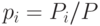 дает возможность рассчитать любую статистическую характеристику набора данных
обучающей выборки.
дает возможность рассчитать любую статистическую характеристику набора данных
обучающей выборки.
Для определения значимости входов нам потребуется оценить предсказуемость выходов, обеспечиваемую данным набором входных переменных. Чем выше эта предсказуемость - тем лучше соответствующий набор входов. Таким образом, метод box-counting предоставляет в наше распоряжение технологию отбора наиболее значимых признаков для нейросетевого моделирования, технологию оптимизации входного пространства признаков.
Согласно общим положениям теории информации, мерой предсказуемости случайной величины  является ее энтропия,
является ее энтропия, 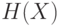 , определяемая
как среднее значение ее логарифма. В методике box-counting энтропия приближенно оценивается по набору чисел заполнения ячеек, на
которые разбивается интервал ее возможных значений:
, определяемая
как среднее значение ее логарифма. В методике box-counting энтропия приближенно оценивается по набору чисел заполнения ячеек, на
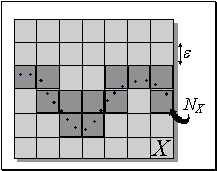
которые разбивается интервал ее возможных значений: 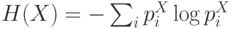 . Качественно, энтропия есть логарифм эффективного числа заполненных ячеек
. Качественно, энтропия есть логарифм эффективного числа заполненных ячеек 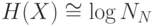 (см. рисунок 7.13). Чем больше энтропия переменной, тем менее предсказуемо ее значение. Когда все
значения примеров сосредоточены в одной ячейке - их энтропия равна нулю, т.к. положение данных определено (с данной степенью точности).
Равномерному заполнению ячеек соответствует максимальная энтропия - наибольший разброс возможных значений переменной.
(см. рисунок 7.13). Чем больше энтропия переменной, тем менее предсказуемо ее значение. Когда все
значения примеров сосредоточены в одной ячейке - их энтропия равна нулю, т.к. положение данных определено (с данной степенью точности).
Равномерному заполнению ячеек соответствует максимальная энтропия - наибольший разброс возможных значений переменной.
Предсказуемость случайного вектора  , обеспечиваемое знанием другой случайной величины
, обеспечиваемое знанием другой случайной величины  , дается кросс-энтропией:
, дается кросс-энтропией: 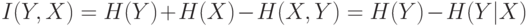
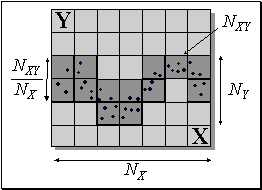
Качественно, кросс-энтропия равна логарифму отношения типичного разброса значений переменной  к типичному разбросу этой
переменной, но при известном значении переменной
к типичному разбросу этой
переменной, но при известном значении переменной  (см.
рисунок 7.14):
(см.
рисунок 7.14): 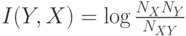 .
.
Чем больше кросс-энтропия, тем больше определенности вносит знание значения  в предсказание значения переменной
в предсказание значения переменной  .
.
Описанный выше энтропийный анализ не использует никаких предположений о характере зависимости между входными и выходными переменными. Таким образом, данная методика дает наиболее общий рецепт определения значимости входов, позволяя также оценивать степень предсказуемости выходов.
В принципе, качество предсказаний и, соответственно, значимость входной информации определяется, в конечном итоге, в результате
обучения нейросети, которая, к тому же, дает решение в явном виде. Однако, как мы знаем, обучение нейросети - довольно сложная
вычислительная задача (требующая 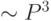 операций). Между тем, существуют эффективные алгоритмы быстрого подсчета кросс-энтропии (с
вычислительной сложностью
операций). Между тем, существуют эффективные алгоритмы быстрого подсчета кросс-энтропии (с
вычислительной сложностью 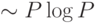 ), намного более экономные, чем обучение нейросетей. Значение методики box-counting состоит в том, что не
находя самого решения, она позволяет быстро предсказать качество этого прогноза. Поэтому эта методика может быть положена в основу
предварительного отбора входной информации на этапе предобработки данных.
), намного более экономные, чем обучение нейросетей. Значение методики box-counting состоит в том, что не
находя самого решения, она позволяет быстро предсказать качество этого прогноза. Поэтому эта методика может быть положена в основу
предварительного отбора входной информации на этапе предобработки данных.