Предобработка данных
Кодирование ординальных переменных
Ординальные переменные более близки к числовой форме, т.к. числовой ряд также упорядочен. Соответственно, для кодирования таких переменных остается лишь поставить в соответствие номерам категорий такие числовые значения, которые сохраняли бы существующую упорядоченность. Естественно, при этом имеется большая свобода выбора - любая монотонная функция от номера класса порождает свой способ кодирования. Какая же из бесконечного многообразия монотонных функций - наилучшая?
В соответствии с изложенным выше общим принципом, мы должны стремиться к тому, чтобы максимизировать энтропию закодированных
данных. При использовании сигмоидных функций активации все выходные значения лежат в конечном интервале - обычно ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) или
или ![[-1,1]](/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) . Из всех
статистических функций распределения, определенных на конечном интервале, максимальной энтропией обладает равномерное распределение.
. Из всех
статистических функций распределения, определенных на конечном интервале, максимальной энтропией обладает равномерное распределение.
Применительно к данному случаю это подразумевает, что кодирование переменных числовыми значениями должно приводить, по возможности, к равномерному заполнению единичного интервала закодированными примерами. (Захватывая заодно и этап нормировки.) При таком способе "оцифровки" все примеры будут нести примерно одинаковую информационную нагрузку.
Исходя из этих соображений, можно предложить следующий практический рецепт кодирования ординальных переменных. Единичный
отрезок разбивается на отрезков - по числу классов - с длинами пропорциональными числу примеров каждого класса в обучающей выборке:  , где
, где 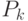 - число примеров класса
- число примеров класса  , а
, а  , как обычно, общее число примеров. Центр каждого такого отрезка будет являться численным
значением для соответствующего ординального класса
(см. рисунок 7.1).
, как обычно, общее число примеров. Центр каждого такого отрезка будет являться численным
значением для соответствующего ординального класса
(см. рисунок 7.1).
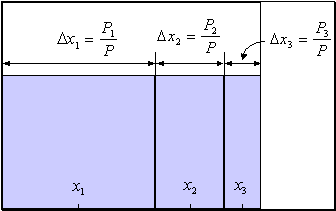
Рис. 7.1. Иллюстрация способа кодирования кардинальных переменных с учетом количества примеров каждой категории
Кодирование категориальных переменных
В принципе, категориальные переменные также можно закодировать описанным выше способом, пронумеровав их произвольным образом. Однако, такое навязывание несуществующей упорядоченности только затруднит решение задачи. Оптимальное кодирование не должно искажать структуры соотношений между классами. Если классы не упорядоченны, такова же должна быть и схема кодирования.
Наиболее естественной выглядит и чаще всего используется на практике двоичное кодирование типа 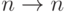 , когда имена
, когда имена  категорий кодируются значениями
категорий кодируются значениями  бинарных нейронов, причем первая категория кодируется как
бинарных нейронов, причем первая категория кодируется как 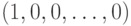 , вторая, соответственно -
, вторая, соответственно - 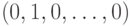 и т.д. вплоть до
и т.д. вплоть до  -ной:
-ной: 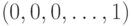 . (Можно использовать биполярную кодировку, в которой нули заменяются на
. (Можно использовать биполярную кодировку, в которой нули заменяются на 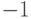 ). Легко убедиться, что в такой симметричной кодировке
расстояния между всеми векторами-категориями равны.
). Легко убедиться, что в такой симметричной кодировке
расстояния между всеми векторами-категориями равны.
Такое кодирование, однако, неоптимально в случае, когда классы представлены существенно различающимся числом примеров. В этом
случае, функция распределения значений переменной крайне неоднородна, что существенно снижает информативность этой переменной. Тогда
имеет смысл использовать более компактный, но симметричный код 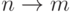 , когда имена
, когда имена  классов кодируются
классов кодируются  -битным двоичным кодом. Причем,
в новой кодировке активность кодирующих нейронов должна быть равномерна: иметь приблизительно одинаковое среднее по примерам значение
активации. Это гарантирует одинаковую значимость весов, соответствующих различным нейронам.
-битным двоичным кодом. Причем,
в новой кодировке активность кодирующих нейронов должна быть равномерна: иметь приблизительно одинаковое среднее по примерам значение
активации. Это гарантирует одинаковую значимость весов, соответствующих различным нейронам.
В качестве примера рассмотрим ситуацию, когда один из четырех классов (например, класс 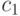 ) некой категориальной переменной
представлен гораздо большим числом примеров, чем остальные:
) некой категориальной переменной
представлен гораздо большим числом примеров, чем остальные: 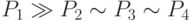 . Простое кодирование
. Простое кодирование 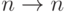 привело бы к тому, что первый нейрон активировался
бы гораздо чаще остальных. Соответственно, веса оставшихся нейронов имели бы меньше возможностей для обучения. Этой ситуации можно
избежать, закодировав четыре класса двумя бинарными нейронами следующим образом:
привело бы к тому, что первый нейрон активировался
бы гораздо чаще остальных. Соответственно, веса оставшихся нейронов имели бы меньше возможностей для обучения. Этой ситуации можно
избежать, закодировав четыре класса двумя бинарными нейронами следующим образом: 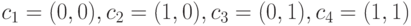 , обеспечивающим равномерную "загрузку"
кодирующих нейронов.
, обеспечивающим равномерную "загрузку"
кодирующих нейронов.
Отличие между входными и выходными переменными
В заключении данного раздела отметим одно существенное отличие способов кодирования входных и выходных переменных, вытекающее из
определения градиента ошибки: ![\frac{\partial E}{\partial w_{ij}^{[n]}}=\delta_i^{[n]}x_j^{[n]}](/sites/default/files/tex_cache/b0d01af4bf1630b352088e493c86a006.png) . А именно, входы участвуют в обучении непосредственно, тогда как выходы - лишь опосредованно - через
ошибку верхнего слоя. Поэтому при кодировании категорий в качестве выходных нейронов можно использовать как логистическую функцию
активации
. А именно, входы участвуют в обучении непосредственно, тогда как выходы - лишь опосредованно - через
ошибку верхнего слоя. Поэтому при кодировании категорий в качестве выходных нейронов можно использовать как логистическую функцию
активации 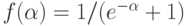 , определенную на отрезке
, определенную на отрезке ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , так и ее антисимметричный аналог для отрезка
, так и ее антисимметричный аналог для отрезка ![[-1,1]](/sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) , например:
, например: 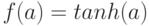 . При этом кодировка выходных
переменных из обучающей выборки будет либо
. При этом кодировка выходных
переменных из обучающей выборки будет либо 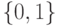 , либо
, либо 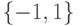 . Выбор того или иного варианта никак не скажется на обучении.
. Выбор того или иного варианта никак не скажется на обучении.
В случае со входными переменными дело обстоит по-другому: обучение весов нижнего слоя сети определяется непосредственно
значениями входов: на них умножаются невязки, зависящие от выходов. Между тем, если с точки зрения операции умножения значения  равноправны, между 0 и 1 имеется существенная асимметрия: нулевые значения не дают никакого вклада в градиент ошибки. Таким образом,
выбор схемы кодирования входов влияет на процесс обучения. В силу логической равноправности обоих значений входов, более
предпочтительной выглядит симметричная кодировка:
равноправны, между 0 и 1 имеется существенная асимметрия: нулевые значения не дают никакого вклада в градиент ошибки. Таким образом,
выбор схемы кодирования входов влияет на процесс обучения. В силу логической равноправности обоих значений входов, более
предпочтительной выглядит симметричная кодировка: 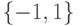 , сохраняющая это равноправие в процессе обучения.
, сохраняющая это равноправие в процессе обучения.
