Нелинейная динамика и синергетика. Искусственный интеллект
Нелинейная динамика и синергетика – возможности применения в параллельных вычислениях
Из результатов исследования электрической активности мозга нейрофизиологами следует, что мозг является нелинейной динамической системой с хаотической природой электрохимических сигналов. Сложная структура коры головного мозга моделируется с помощью взаимосвязанных нейронных решеток. Глобальная связь между нейронами порождает их коллективное поведение. Каждый нейрон представляет собой отдельное устройство, которое можно сопоставить процессору вычислителя. Именно поэтому структура нейронной сети наиболее подходит для выполнения параллельных вычислений, поскольку нет необходимости в предварительной подготовке исходных данных перед распараллеливанием.
Десятки сотен проектов, направленных на исследование принципов функционирования головного мозга человека, также способствовали становлению новой предметной области — нелинейной динамики. Нелинейная динамика — это часть синергетики, которая изучает коллективное поведение множества нелинейных объектов: квантов, атомов, молекул, клеток (в частности нейронов), подсистем. Одним из направлений в нелинейной динамике является изучение проявления самоорганизации в синхронизации хаотических систем. Изучение синхронизации — этого фундаментального явления природы — проводится в биохимии, биофизике, квантовой физике, нейропсихологии, нейрофизиологии, нейробиологии.
Отметим, что исследования все более приобретают междисциплинарный характер. Поскольку всё связано со всем, то закономерности, которые выявляются в поведении и функционировании элементов одной природы, иногда могут быть использованы для управления элементами другой природы. Как показывают многочисленные исследования в области нелинейной динамики — чем сложнее задача, тем сложнее динамика системы, и, следовательно, управление ею. Поэтому все больше работ посвящено объединению достижений в области нелинейной динамики, самоорганизации и теории нейронных сетей.
При разработке новых высокопроизводительных систем на основе принципов самоорганизации предполагается, что решение задачи и соответствующая структура для ее решения самоорганизуются за счет внутренних процессов в системе и за счет обратной связи с внешней средой — классических задач низкоуровневой функциональной декомпозиции в данном случае не возникает [Амелин К. С., Граничин О. Н., Кияев В. И., 2010]. Более того, использование синергетического синтеза также предполагает отсутствие классического разделения в вычислениях на аппаратную и программную части.
Такое вычислительное устройство, как было сказано выше, может представлять собой набор асинхронных моделей динамических систем, взаимодействующих между собой и сочетающих такие свойства, как гибридность, асинхронность, кластерность, стохастичность [Вахитов А. Т., Граничин О. Н., Сысоев С. С., 2006].
О. Н. Граничин и его соавторы предложили и обосновали новую абстракцию вычислительного устройства, обобщающую схему классической машины Тьюринга [Граничин О. Н., Молодцов С. Л., 2006; Граничин О. Н., Васильев В. И., 2010]. В рамках новой модели переосмысливаются ставшие традиционными понятия "такт", "память", "ленты", "программы" и "состояния".
Если в классическом подходе ячейки памяти используются для хранения дискретной информации и их изменение возможно только в тех случаях, когда указатель ленты показывает на нее, то в новой концепции "ячейка памяти" представляет собой постоянно функционирующую модель достаточно сложной динамической системы, а "лента" — подмножество в общем пространстве состояний, при достижении которого заканчивается очередной "такт" и происходит включение "программы" — скачкообразное переключение с одних моделей на другие. Естественно, что классическая ячейка памяти для хранения единицы информации ("бита") является частным случаем такого обобщения.
В любых современных вычислительных устройствах хранение информации основано на тех или иных физических принципах, только эволюция состояния ячейки во время хранения более простая — сохраняется постоянной какая-то физическая характеристика. Другими словами, поле вычислений в традиционной информатике можно сравнить с арифметикой, она оперирует цифрами — значениями ячеек памяти (или, более точно — арифметикой конечных двоичных дробей). Предлагаемая новая модель вычислений позволит перейти в информатике от "арифметики" к "функциональному анализу", исследующему процессы эволюции информации внутри новых "ячеек" (операции с функциями).
Другим обобщением может быть вероятностное задание отображений эволюции и программ, что позволит реализовывать с помощью новой модели динамические системы, стохастические гибридные системы, вероятностные автоматы, системы со стохастическим управлением, то есть системы, не описываемые детерминированными законами. Для организации работы такой вычислительной системы, наверное, целесообразно будет использовать рандомизацию, позволяющую частично устранить влияние на работу системы систематических погрешностей, которые практически неизбежны при изменяющейся со временем модели динамической системы.
Предлагаемая новая модель вычислений позволяет описывать если не все, то подавляющее большинство процессов реального мира, а также работу всевозможных существующих и будущих вычислительных устройств, включая аналоговые и биокомпьютеры, нейрокомпьютеры, квантовые компьютеры и т. д. Особенностью рассматриваемого подхода является отказ от редукции сложности в процессе вычисления. Сложность вычислимого объекта должна быть эквивалентна сложности вычисляемого.
Другими словами, понятие вычислительной сложности правильнее рассматривать относительно выбранной системы базисных эволюционных примитивов, а не относительно традиционно рассматриваемых битовых преобразований {0;1}. Квантовые и нейрокомпьютеры обещают сильно изменить представления о вычислительной мощности современных вычислительных устройств. Увеличение вычислительной мощности, возможное за счет использования новых моделей вычислений, основывающихся на физических явлениях, позволяет предположить, что в будущем новые компьютеры смогут решать задачи, невыполнимые для обычных компьютеров.
Модель вычислений для такого устройства можно свести к совокупности следующих базовых параметров:
- набор вычислительных примитивов (динамические модели Hi с параметрами Q);
- память X — общее пространство состояний всех моделей;
- лента S — динамический граф с конечной битовой строкой s "включения" моделей в узлах;
- программа G — заданные на графе S правила (или цели) переключения "ленты" и параметров моделей при попадании пары (x, q) на одном из "включенных" узлов в множество переключения J;
- такт — промежуток времени между соседними моментами переключений;
- множество останова T .
В этом случае уместно говорить об обобщенной машине Тьюринга, которую можно представить в виде кортежа взаимосвязанных компонентов 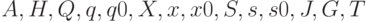 , где
, где  — множество моделей (вычислительных примитивов),
— множество моделей (вычислительных примитивов),  — оператор эволюции,
— оператор эволюции,  — множество состояний (значений параметров),
— множество состояний (значений параметров),  — память,
— память,  — обобщенная лента (граф),
— обобщенная лента (граф), 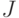 — множество переключений,
— множество переключений,  — программа (цели),
— программа (цели),  — множество останова [Владимирович А. Г., Граничин О. Н., Макаров А. А., 2005].
— множество останова [Владимирович А. Г., Граничин О. Н., Макаров А. А., 2005].
Здесь можно также отметить взаимное сближение технологий разработки программного и аппаратного обеспечения. Это связано с широким распространением программируемых архитектур, в которых, тоже используется большое число относительно простых ячеек, которые программируется под определенные функции путем определенного связывания друг с другом. В связи с этим получили развитие языки аппаратного программирования, процедуры отладки и среды разработки как в программном обеспечении. Программирование, отладка тестирование при разработке аппаратуры оказываются очень схожими с разработкой программных комплексов.
Еще одно из активно развиваемых и используемых решений для высокопроизводительных вычислений — платы компьютерной графики, содержащие огромное число не слишком сложных графических процессоров-вычислителей. Первоначально такие процессоры были предназначены для ускорения работы приложений компьютерной графики, у которой задачи принципиально параллельны и требуют одновременной обработки всех компонент графической картинки. Однако эти структуры оказались очень эффективным средством для решения задач вычислительной физики и параллельного проведения экспериментов и для нейровычислений. Правда надо отметить, что для использования возможностей графических ускорителей также необходимо знание и использование специального языка обращений к матрице графических процессоров. Но так как логический базис операций этих процессоров естественным образом оказался совместим с требуемыми операциями при проведении нейровычислений и других параллельно представленных задач, то этот подход использования графических ускорителей, при условии дальнейшего совершенствования средств их программирования, будет получать все большее и большее распространение.
Кроме того, существует такая тенденция, как придание аппаратной реализации большей гибкости — разработка процессоров и многопроцессорных архитектур с переменной структурой. И здесь также есть решения на уровне переменной организации отдельного элемента, так и для всей структуры из большого числа элементов. Это согласуется с теми тенденциями, которые можно наблюдать в развитии идей нейровычислений. В нейронных сетях структура нейронной сети адаптируется под решаемую задачу как в малом — на уровне отдельных весовых коэффициентов в пределах заданной структуры, так и в большом — при отсутствии ограничений на композицию нейронных ансамблей.
Вместо привычного представления исходной задачи, подлежащей решению в виде совокупности функций, для последующей реализации, или разделении системы на отдельные части, при синергетическом походе проводится синтез и исследование системы как единого целого. Изменение состояния отдельного элемента системы может никак не повлиять на состояние системы в целом, однако, совместная динамика всех элементов определяет макроскопическое уникальное состояние системы. И это состояние системы и будет являться решением поставленной задачи [Бендерская Е.Н., Граничин О. Н., Кияев В. И., 2012; Бендерская Е. Н., Граничин О. Н., Кияев В. И., 2013].
Именно возникновение синхронизации, коллективного поведения позволяет живым системам адаптироваться, обучаться, извлекать информацию и в реальном времени решать вычислительно сложные задачи за счет распределенной обработки информации. Много элементов со сложной динамикой порождают эффективные вычисления.
