Нелинейная динамика и синергетика. Искусственный интеллект

В других случаях в задачах о наблюдении физических явлений часто достаточно обоснованно предполагают статистическую природу помех, но возможны осмысленные постановки задачи и при произвольных внешних помехах [Граничин О. Н. , Поляк Б. Т., 2003].

Сложившаяся к настоящему времени парадигма использования вычислительных устройств базируется на исторически сложившемся разделении процессов обработки данных и принятия управленческих решений (после обработки). Основания этого разделения прослеживаются в истории развития средств вычислительной техники. Первоначально компьютеров было мало и они, занимая огромные пространства, требовали специальных условий для эксплуатации. Формировались особые вычислительные центры для объединенного решения в одном месте множества разных задач, причем до сих пор актуальным остается одно из приоритетных направлений развития — создание суперкомпьютеров. Встроенным устройствам традиционно отводилась роль или устройств для сбора данных, или устройств для реализации определенных управляющих воздействий. В некоторых случаях они использовались как регуляторы в простых контурах обратной связи. Суперкомпьютеры брали на себя выполнение задач Data Mining.

Но надо четко отдавать себе отчет в применимости этой традиционной парадигмы. В природе и обществе информационно-управленческие связи являются основой связи многих явлений и процессов. Искусственно разделяя процессы обработки данных и управления, мы существенно снижаем наши возможности использования информационно-коммуникационных технологий.

Надо ли разделять процессы обработки данных и управления?

С начала XXI века в теории управления заметен всплеск интереса к тематике поиска данных, управления в сетях, коллективному взаимодействию, мультиагентным технологиям и т.п. Это во многом связано с технологическим прогрессом. Сейчас миниатюризация и быстродействие средств вычислительной техники достигли такого уровня, что стало возможным в миниатюрных встроенных системах реального времени использовать вычислительные блоки, соизмеримые по производительности с мощными компьютерами XX веке. Все чаще "простые" встроенные электронные устройства заменяются сложнейшими "интеллектуальными встроенными системами".

Новые альтернативы и новые технологии позволяют по-новому взглянуть на ставшую уже традиционной область поиска и извлечения данных (Data Mining). В литературе все чаще появляются мысли о возрождении науки "Кибернетика" с большой буквы, о появлении "неокибернетики" [Соколов Б. В., Юсупов Р. М. , 2008].

Теория управления начала свой путь с регуляторов механических систем в XIX века. К концу ХХ века она прошла этап глубокой интеграции с цифровыми технологиями обработки данных и принятия решений, а в XXI веке стала фокусироваться на сетях объектов. В настоящее время теория управления выступает "собирателем" трех основных компонент прогресса второй половины ХХ века [Андриевский Б. Р. , Матвеев А. С. , Фрадков А. Л. , 2006]:

• теории управления (Control Theory),
• теории коммуникаций (Communication Theory)
• информатики (Computer Science)

Таким образом, применение кибернетической парадигмы, при которой процессы "добычи знаний" и получения информации будут учитывать неразрывную связь информации и управления и опираться на нее, обязательно приведут к формированию нового качества в обработке данных и извлечении знаний. Тогда можно поставить следующий вопрос: может ли дать какое-то новое качество в обработке данных и извлечении знаний применение кибернетической парадигмы, при которой процессы получения информации и "добычи знаний" и будут учитывать неразрывную связь информации и управления (и опираться на нее)?

Для иллюстрации положительного ответа в книге О. Н. Граничина и соавторов [Граничин О. Н., 2014] рассмотрены несколько примеров повышения эффективности процессов обработки данных и управления при изменении вычислительной парадигмы. Один из них основан на использовании замкнутых стратегий управления в условиях неопределенностей. 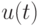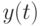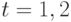Для объекта управления (ОУ) с входами и выходами , и предположим, что задано начальное состояние , и динамика объекта при описывается уравнением

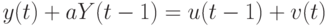
с неопределенностями и a двух типов:

• динамические возмущения неизвестны и ограничены для всех : 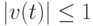, но могут меняться со временем;
• коэффициент модели также неизвестен и ограничен: , но он не может изменяться со временем.

Можно выбрать входы и 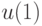. Цель – минимизировать .

При сравнении качества минимаксной оптимизации

.

для двух классов допустимых стратегий управления: программных (всевозможные пары , ) и замкнутых (в которых в момент времени можно использовать наблюдение 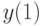и управление ), получились два существенно отличающихся ответа 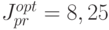и .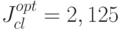

Зависимость качества управления от задания класса неупреждающих стратегий адекватно понимается далеко не всех публикациях. Если все параметры объекта управления известны и помехи отсутствуют, то множества программных и замкнутых стратегий управления оказываются совпадающими.

Другой пример из той же книги О.Н. Граничина и соавторов показывает возможность получения обоснованных оценок неизвестных параметров системы в условиях произвольных внешних возмущений в измерениях при допущении возможности активно влиять на результаты измерений, выбирая рандомизированные управления (входы).

В случае больших и сложных систем, состоящих из похожих компонентов, в статистической механике и физике оправдал себя подход Крылова-Боголюбова, основанный на усреднении данных, активно развиваемый, начиная с работ Гиббса, основываясь на теории Лебега. Для большого количества физических и социальных явлений при отсутствии внешних воздействий выполняется гипотеза эргодичности, когда среднее пространственное значение той или иной характеристики различных компонент системы, подсчитанное в определенный момент времени, совпадает со средним временным значением одной из компонент. При этом идеи усреднения хорошо согласуются и с конструкцией многих регистрирующих приборов, принцип действия которых часто заключается в том, что они выдают в результате некоторое среднее значение той или иной характеристики за определенный интервал времени.

Если регистрирующий прибор усредняет поступающие при 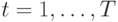"мгновенные" сигналы с помехами , то на выходе прибора получаем

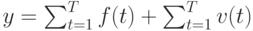
При случайной природе помех и известном среднем значении m в предположении об их независимости, одинаковой распределенности, конечности дисперсии, в силу закона больших чисел теории вероятностей, увеличивая , можно добиться сколь угодно малой вероятности отличия второго слагаемого в последней формуле от среднего значения помехи. Т.е. по данным и можно достаточно точно определить среднее значение сигнала , определяемое первым слагаемым в последней формуле.

Что делать, если помехи не являются случайными (статистическими)? Например, — значения неизвестной функции (т.е. произвольные значения).

В рамках классической парадигмы обработки данных постановка задачи об оценивании среднего значения сигнала регистрируемого на фоне произвольных помех кажется абсурдной, но не из-за ее практической бессмысленности (это очень важная задача), а из-за невозможности ее как-то решить.

Для простоты рассмотрим случай скалярных наблюдений. Модернизируем постановку задачи, включив в модель наблюдений управляющее воздействие (вход) .

Следуя парадигме неразрывности информации и управлений, будем считать, что регистрируемый сигнал в момент времени напрямую определяется текущим входом 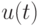и некоторым неизвестным параметром (неизвестным коэффициентом усиления/ослабления входа)

.

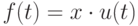Модель наблюдений можно переписать в виде:

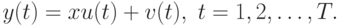
При этом мы можем: а). выбирать входы 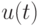, б). измерять выходы .

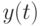При использовании получаем традиционную задачу об оценивании неизвестного параметра , наблюдаемого на фоне помех.