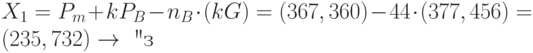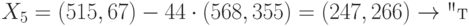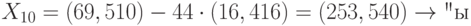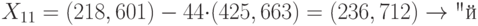|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы с открытыми ключами
8.6 Шифрование на основе группы точек эллиптической кривой
Опишем аналоги некоторых широко распространенных систем с открытым ключом, основанные на задаче дискретного логарифмирования на эллиптической кривой, определенной над конечным полем 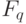 .
.
8.6.1 Ключевой обмен
Предположим, что абоненты А и Б хотят договориться о ключе, которым будут впоследствии пользоваться в некоторой классической криптосистеме. Прежде всего, они открыто выбирают какое-либо конечное поле 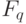 (
(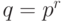 ) и какую-либо эллиптическую кривую
) и какую-либо эллиптическую кривую  над ним. Их ключ строится по случайной точке
над ним. Их ключ строится по случайной точке  на этой эллиптической кривой. Если у них есть случайная точка
на этой эллиптической кривой. Если у них есть случайная точка  , то, например, ее
, то, например, ее  -координата дает случайный элемент
-координата дает случайный элемент 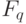 , который можно затем преобразовать в
, который можно затем преобразовать в  -разрядное целое число в
-разрядное целое число в  -ричной системе счисления, и это число может служить ключом в их классической криптосистеме. Они должны выбрать точку
-ричной системе счисления, и это число может служить ключом в их классической криптосистеме. Они должны выбрать точку  так, чтобы все их сообщения друг другу были открытыми и все же никто, кроме них двоих, ничего бы не знал о
так, чтобы все их сообщения друг другу были открытыми и все же никто, кроме них двоих, ничего бы не знал о  .
.
Абоненты (пользователи) А и Б первым делом открыто выбирают точку 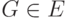 в качестве "основания". Чтобы образовать ключ, абонент А вначале случайным образом выбирает целое число
в качестве "основания". Чтобы образовать ключ, абонент А вначале случайным образом выбирает целое число  , это число он держит в секрете. Он вычисляет
, это число он держит в секрете. Он вычисляет 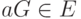 и передает эту точку открыто. Абонент Б делает то же самое: он выбирает случайно
и передает эту точку открыто. Абонент Б делает то же самое: он выбирает случайно  и открыто передает
и открыто передает 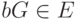 . Тогда используемый ими секретный ключ - это
. Тогда используемый ими секретный ключ - это 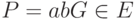 . Оба пользователя могут вычислить этот ключ. Например, абонент А знает
. Оба пользователя могут вычислить этот ключ. Например, абонент А знает 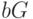 (точка была передана открыто) и свое собственное секретное a. Однако любая третья сторона знает лишь
(точка была передана открыто) и свое собственное секретное a. Однако любая третья сторона знает лишь 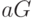 и
и 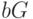 .
Кроме решения задачи дискретного логарифмирования - нахождения
.
Кроме решения задачи дискретного логарифмирования - нахождения  по
по  и
и 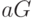 (или нахождения
(или нахождения  по
по  и
и 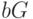 ) - по-видимому, нет способа найти
) - по-видимому, нет способа найти 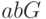 , зная лишь
, зная лишь 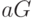 и
и 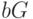 .
.
Пример 8.14 Возьмём эллиптическую кривую 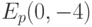 , где
, где 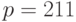 , и точку
, и точку 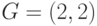 . Произведём обмен ключами.
. Произведём обмен ключами.
Личным ключом пользователя А является 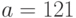 , поэтому его открытым ключом будет
, поэтому его открытым ключом будет 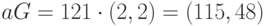 . Личным ключом пользователя Б является
. Личным ключом пользователя Б является 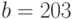 , поэтому его открытым ключом будет
, поэтому его открытым ключом будет 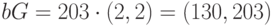 . Общим секретным ключом является
. Общим секретным ключом является

Общий секретный ключ представляет собой пару чисел. Если этот ключ предполагается использовать в качестве сеансового ключа для традиционного шифрования, то из этой пары чисел необходимо генерировать одно подходящее значение. Можно, например, использовать просто координату  или некоторую простую функцию от
или некоторую простую функцию от  .
.
Криптосистема с открытым ключом для передачи сообщений
Как и в описанной выше системе ключевого обмена, мы исходим из несекретных данных:
- конечного поля
 ;
; - определенной над ним эллиптической кривой
 ;
; - точки-"основания" $G$ на ней (знать общее число
 точек на
точек на  не нужно).
не нужно).
Каждый из пользователей выбирает случайное целое число: 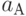 - у пользователя А, и
- у пользователя А, и  - у пользователя Б, которое пользователь держит в секрете. Затем пользователи А и Б вычисляют точки, соответственно,
- у пользователя Б, которое пользователь держит в секрете. Затем пользователи А и Б вычисляют точки, соответственно, 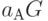 и
и  .
.
Чтобы послать пользователю Б сообщение 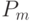 , пользователь А выбирает случайно целое число
, пользователь А выбирает случайно целое число  и посылает пару точек
и посылает пару точек 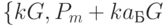 (где
(где  - открытый ключ пользователя Б). Чтобы прочитать сообщение, пользователь Б умножает первую точку из полученной пары на свое секретное число
- открытый ключ пользователя Б). Чтобы прочитать сообщение, пользователь Б умножает первую точку из полученной пары на свое секретное число  и вычитает результат умножения из второй точки:
и вычитает результат умножения из второй точки:
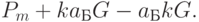
Таким образом, пользователь А посылает замаскированное сообщение 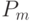 вместе с "подсказкой"
вместе с "подсказкой" 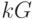 , при помощи которой можно снять "маску"
, при помощи которой можно снять "маску"  , если знать секретное число
, если знать секретное число  . Злоумышленник, который умеет решать задачу дискретного логарифмирования на
. Злоумышленник, который умеет решать задачу дискретного логарифмирования на  , может, конечно, найти
, может, конечно, найти  , зная
, зная  и
и  .
.
Пример 8.15 Рассмотрим кривую 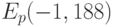 с
с 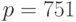 (что соответствует кривой
(что соответствует кривой  ) и точкку
) и точкку  . Предположим, что пользователь А собирается отправить пользователю Б сообщение, которое кодируется эллиптической точкой
. Предположим, что пользователь А собирается отправить пользователю Б сообщение, которое кодируется эллиптической точкой  , и что пользователь А выбирает случайное число
, и что пользователь А выбирает случайное число 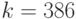 . Открытым ключом пользователя Б является
. Открытым ключом пользователя Б является  .
.
Мы имеем
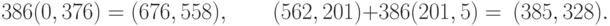
Таким образом, пользователь А должен послать шифрованный текст: {(676, 558), (385, 328)}.
8.6.2 Пример кодирования и декодирования текста
См. [3]
Перед шифрованием необходимо выбрать способ кодирования текста. Для этого найдем точки на кривой и некоторым из них поставим в соответствие символы.
Выберем кривую  , т. е.
, т. е. 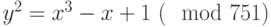 . Таблица 8.3 задаёт соответствие символов и некоторых точек кривой.
. Таблица 8.3 задаёт соответствие символов и некоторых точек кривой.
| № | Символ | Точка | № | Символ | Точка | № | Символ | Точка |
|---|---|---|---|---|---|---|---|---|
| 1 | пробел | (33, 355) | 54 | U | (80, 433) | 107 | Л | (200, 721) |
| 2 | ! | (33, 396) | 55 | V | (82, 270) | 108 | М | (203, 324) |
| 3 | " | (34, 74) | 56 | W | (82, 481) | 109 | Н | (203, 427) |
| 4 | # | (34, 677) | 57 | X | (83, 373) | 110 | О | (205, 372) |
| 5 | $ | (36, 87) | 58 | Y | (83, 378) | 111 | П | (205, 379) |
| 6 | % | (36, 664) | 59 | Z | (85, 35) | 112 | Р | (206, 106) |
| 7 | & | (39, 171) | 60 | [ | (85, 716) | 113 | С | (206, 645) |
| 8 | ' | (39, 580) | 61 | \ | (86,25) | 114 | Т | (209, 82) |
| 9 | ( | (43, 224) | 62 | ] | (86, 726) | 115 | У | (209, 669) |
| 10 | ) | (43, 527) | 63 |  |
(90,21) | 116 | Ф | (210, 31) |
| 11 | * | (44, 366) | 64 | _ | (90, 730) | 117 | Х | (210, 720) |
| 12 | + | (44, 385) | 65 | ' | (93, 267) | 118 | Ц | (215, 247) |
| 13 | , | (45, 31) | 66 | a | (93, 484) | 119 | Ч | (215, 504) |
| 14 | - | (45, 720) | 67 | b | (98, 338) | 120 | Ш | (218,150) |
| 15 | . | (47, 349) | 68 | c | (98, 413) | 121 | Щ | (218, 601) |
| 16 | / | (47, 402) | 69 | d | (99, 295) | 122 | Ъ | (221, 138) |
| 17 | 0 | (48,49) | 70 | e | (99, 456) | 123 | Ы | (221, 613) |
| 18 | 1 | (48, 702) | 71 | f | (100, 364) | 124 | Ь | (226, 9) |
| 19 | 2 | (49, 183) | 72 | g | (100, 387) | 125 | Э | (226, 742) |
| 20 | 3 | (49, 568) | 73 | h | (102, 267) | 126 | Ю | (227, 299) |
| 21 | 4 | (53, 277) | 74 | i | (102, 484) | 127 | Я | (227, 452) |
| 22 | 5 | (53, 474) | 75 | j | (105, 369) | 128 | а | (228, 271) |
| 23 | 6 | (56, 332) | 76 | k | (105,382) | 129 | б | (228, 480) |
| 24 | 7 | (56, 419) | 77 | l | (106, 24) | 130 | в | (229, 151) |
| 25 | 8 | (58, 139) | 78 | m | (106, 727) | 131 | г | (229, 600) |
| 26 | 9 | (58, 612) | 79 | n | (108, 247) | 132 | д | (234, 164) |
| 27 | : | (59, 365) | 80 | o | (108, 504) | 133 | е | (234, 587) |
| 28 | ; | (59, 386) | 81 | p | (109, 200) | 134 | ж | (235, 19) |
| 29 | < | (61, 129 | 82 | q | (109, 551) | 135 | з | (235, 732) |
| 30 | = | (61, 622) | 83 | r | (110, 129) | 136 | и | (236, 39) |
| 31 | > | (62, 372) | 84 | s | (110, 622) | 137 | й | (236, 712) |
| 32 | ? | (62, 379) | 85 | t | (114, 144) | 138 | к | (237, 297) |
| 33 | @ | (66, 199) | 86 | u | (114, 607) | 139 | л | (237, 454) |
| 34 | A | (66, 552) | 87 | v | (115, 242) | 140 | м | (238, 175) |
| 35 | B | (67,84) | 88 | w | (115, 509) | 141 | н | (238, 576) |
| 36 | C | (67, 667) | 89 | x | (116, 92) | 142 | о | (240, 309) |
| 37 | D | (69, 241) | 90 | y | (116, 659) | 143 | п | (240, 442) |
| 38 | E | (69, 510) | 91 | z | (120, 147) | 144 | р | (243, 87) |
| 39 | F | (70, 195) | 92 | { | (120, 604) | 145 | с | (243, 664) |
| 40 | G | (70, 556) | 93 | _ | (125, 292) | 146 | т | (247, 266) |
| 41 | H | (72, 254) | 94 | } | (125, 459) | 147 | у | (247, 485) |
| 42 | I | (72, 497) | 95 | 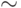 |
(126, 33) | 148 | ф | (249, 183) |
| 43 | J | (73,72) | 96 | А | (189, 297) | 149 | х | (249, 568) |
| 44 | K | (73, 679) | 97 | Б | (189, 454) | 150 | ц | (250, 14) |
| 45 | L | (74, 170) | 98 | В | (192, 32) | 151 | ч | (250, 737) |
| 46 | M | (74, 581) | 99 | Г | (192, 719) | 152 | ш | (251, 245) |
| 47 | N | (75, 318) | 100 | Д | (194, 205) | 153 | щ | (251, 506) |
| 48 | O | (75, 433) | 101 | Е | (194, 546) | 154 | ъ | (253, 211) |
| 49 | P | (78, 271) | 102 | Ж | (197, 145) | 155 | ы | (253, 540) |
| 50 | Q | (78, 480) | 103 | З | (197, 606) | 156 | ь | (256, 121) |
| 51 | R | (79, 111) | 104 | И | (198, 224) | 157 | э | (256, 630) |
| 52 | S | (79, 640) | 105 | Й | (198, 527) | 158 | ю | (257, 293) |
| 53 | T | (80, 318) | 106 | К | (200, 30) | 159 | я | (257, 458) |
Заметим, что мощность множества точек на этой кривой 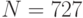 , поэтому при необходимости можно точками закодировать и некоторые специальные знаки (например, знак интеграла и т. п.), а также целые слова.
, поэтому при необходимости можно точками закодировать и некоторые специальные знаки (например, знак интеграла и т. п.), а также целые слова.
Приведем примеры решения контрольных заданий, представленных ниже.
Пример 8.16 (Шифрование) Пусть выбрана генерирующая точка  . Предположим, пользователь
. Предположим, пользователь  решил отправить пользователю
решил отправить пользователю  сообщение: строчную латинскую букву "A". В нашем алфавите эта буква кодируется точкой
сообщение: строчную латинскую букву "A". В нашем алфавите эта буква кодируется точкой  . Пусть пользователь
. Пусть пользователь  выбрал случайное значение
выбрал случайное значение  , а открытым ключом
, а открытым ключом  является точка
является точка 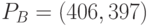 , при этом секретным ключом
, при этом секретным ключом  является число
является число  .
.
Шифрованный текст имеет вид 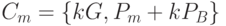 .
.
Находим 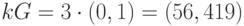 .
.
Вычисляем 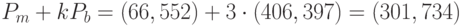 .
.
В результате: 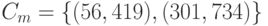 .
.
Пользователь  для расшифрования сообщения должен провести следующие вычисления:
для расшифрования сообщения должен провести следующие вычисления:

После этого пользователь B по алфавиту определяет открытый буквенный текст: точке (66, 552) соответствует строчная латинская буква A.
Пример 8.17 Кривая: 
Генерирующая точка: 
Открытый текст: "терновник"
Открытый ключ: 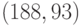
Значения случайных чисел  для букв открытого текста:
для букв открытого текста: 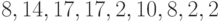 .
.
Установим соответствие точек кривой буквам:
т  (247, 266) (247, 266) |
н  (238, 576) (238, 576) |
н  (238, 576) (238, 576) |
е 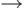 (234, 587) (234, 587) |
о 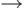 (240, 309) (240, 309) |
и 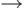 (236, 39) (236, 39) |
р 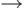 (243, 87) (243, 87) |
в  (229, 151) (229, 151) |
к  (237, 297) (237, 297) |
Расчёт:
Установим соответствие букв и точек шифрованного текста:
| Т | (346, 242), (594, 414) |
| е | (596, 433), (34, 677) |
| р | (440, 539), (546, 670) |
| н | (440, 539), (694, 581) |
| о | (188, 93), (515, 684) |
| в | (377, 456), (517, 573) |
| н | (346, 242), (288, 639) |
| и | (188, 93), (209, 82) |
| к | (188, 93), (205, 379) |
Шифртекст: {(346, 242), (594, 414)}; {(596, 433), (34, 677)}; {(440, 539), (546, 670)}; {(440, 539), (694, 581)}; {(188, 93), (515, 684)}; {(377, 456), (517, 573)}; {(346, 242), (288, 639)}; {(188, 93), (209, 82)}; {(188, 93), (205, 379)}.
Пример 8.18 (Расшифрование) Входные данные.
Кривая: 
Генерирующая точка: 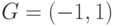
Шифртекст: {(377, 456), (367, 360)}, {(425, 663), (715, 398)}; {(188, 93), (279, 353)}, {(179, 275), (128,79)}; {(568, 355), (515, 67)}, {(568, 355), (482, 230)}; {(377, 456), (206, 645)}, {(188, 93), (300, 455)}; {(489, 468), (362, 446)}, {(16, 416), (69, 510)}; {(425, 663), (218,601)}.
Секретный ключ: 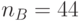 .
.
Расчёт:
Открытый текст - "заостренный".
Список литературы
- Маховенко Е.Б. Теоретико-числовые методы в криптографии -- М.: Гелиос АРВ, 2006.
- Шнайер Б. Прикладная криптография. Протоколы, алгоритмы, исходные тексты на языке Си -- М.: Триумф, 2003. -- 816 с.
- Жданов О.Н., Чалкин В.А. Эллиптические кривые. Основы теории и криптографические приложения -- М.: УРСС, 2013.
- Жданов О.Н., Лубкин И.А. Алгоритм RSA. Методические указания -- Красноярск: СибГАУ, 2007.
- Diffie, W., Hellman, M.E. New Directions in Cryptography // IEEE Transactions on Information Theory. -- v. IT--22(Nov 1976). -- \textnumero 6. -- p. 644--654.
- Rivest, R. L., Shamir, A., Adleman, L. A method for obtaining digital signatures and public-key cryptosystems // Communications of the ACM. --- V. 21 (Feb. 1978). --- \textnumero 2. -- pp. 120—126.
- Столлингс В. Криптография и защита сетей -- М.: Вильямс, 2001. -- 672 с.
- Иванов М.А. Криптографические методы защиты информации в компьютерных системах и сетях -- М.: КУДИЦ-ОБРАЗ, 2001. -- 368 с.

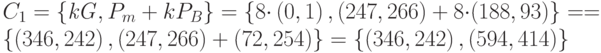 ;
;
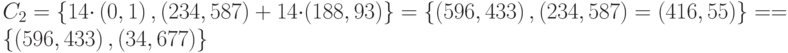 ;
;
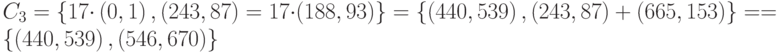 ;
;
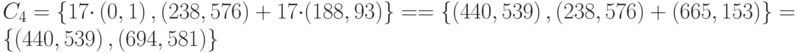 ;
;
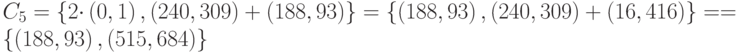 ;
;
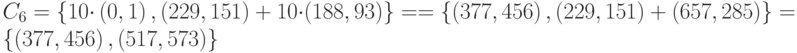 ;
;
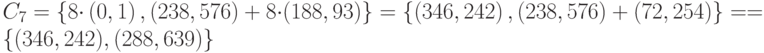 ;
;
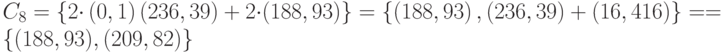 ;
;
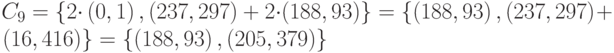 .
.