|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы с открытыми ключами
8.4 Рюкзачный шифр
См. [2]
Схема рюкзака несложна. Дана куча предметов различной массы, можно ли положить некоторые их этих предметов в рюкзак так, чтобы масса рюкзака стала равна определенному значению? Более формально: дан набор значений 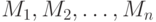 и сумма
и сумма  . Нужно вычислить значения
. Нужно вычислить значения 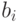 такие, что
такие, что 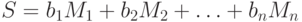 , где
, где 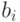 может быть либо нулем, либо единицей. Единица показывает, что предмет кладут в рюкзак, а ноль - что не кладут.
может быть либо нулем, либо единицей. Единица показывает, что предмет кладут в рюкзак, а ноль - что не кладут.
Например, массы предметов могут иметь значения 1, 5, 6, 11, 14 и 20. Вы можете упаковать рюкзак так, чтобы его масса стала равна 22, использовав массы 5, 6 и 11. Невозможно упаковать рюкзак так, чтобы его масса была равна 24. В общем случае время, необходимое для решения этой проблемы, с ростом количества предметов в куче растет экспоненциально.
В основе алгоритма рюкзака Меркла-Хеллмана лежит идея шифровать сообщение как решение набора проблем рюкзака. Предметы из кучи выбираются с помощью блока открытого текста, по длине равного количеству предметов в куче (биты открытого текста соответствуют значениям 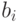 ), а шифртекст является полученной суммой. Пример шифртекста, зашифрованного с помощью рюкзака в таблице 8.2.
), а шифртекст является полученной суммой. Пример шифртекста, зашифрованного с помощью рюкзака в таблице 8.2.
| Открытый текст | 111001 | 010110 | 000000 | 011000 |
| Рюкзак | 1,5,6,11,14,20 | 1,5,6,11,14,20 | 1,5,6,11,14,20 | 1,5,6,11,14,20 |
| Шифртекст | 1+5+6+20=32 | 1+11+14=30 | 0=0 | 5+6=11 |
На самом деле существуют две различные проблемы рюкзака, одна решается за линейные время, а другая, как считается,нет. Легкую проблему можно превратить в трудную. Открытый ключ предоставляет собой трудную проблему, которую легко использовать для шифрования, но невозможно для расшифрования сообщений. Закрытый ключ является легкой проблемой, давая простой способ расшифровать сообщения. Тому, кто не знает закрытый ключ, придется попытаться решить трудную проблему рюкзака.
8.4.1 Сверхвозрастающие рюкзаки
Если перечень масс представляет собой сверхвозрастающую последовательность, то полученную проблему рюкзака легко решить. Сверхвозрастающая последовательность - это последовательность, в которой каждой член больше суммы всех предыдущих членов. Например, последовательность {1,3,6,13,27,52} является сверхвозрастающей, а {1,3,4,9, 15,25} - нет.
Решение сверхвозрастающего рюкзака найти легко. Возьмите полный вес и сравните его с самым большим числом последовательности. Если полный вес меньше, чем это число, то его не кладут в рюкзак. Если полный вес больше или равен этому числу, то оно кладется в рюкзак. Уменьшим массу рюкзака на это значение и перейдем к следующему по величине числу последовательности. Будем повторять, пока процесс не закончится. Если полный вес уменьшится до нуля, то решение найдено. В противном случае нет.
Например, пусть полный вес рюкзака - 70, а последовательность весов {2,3,6, 13,27,52}. Самый большой вес, 52, меньше 70, поэтому кладем 52 в рюкзак. Вычитая 52 из 70, получаем 18. Следующий вес - 27, больше 18, поэтому 27 в рюкзак не кладется. Вес 13, меньше 18, поэтому кладем 13 в рюкзак. Вычитая 13 из 18, получаем 5. Следующий вес - 6, больше 5, поэтому 6 не кладется в рюкзак. Продолжение этого процесса покажет, что и 2, и 3 кладутся в рюкзак, и полный вес уменьшается до 0, что сообщает о найденном решении. Если бы это был блок шифрования методом рюкзака Меркла-Хеллмана, открытый текст, полученный из значения шифртекста 70, был бы равен 110101.
Не сверхвозрастающие, или нормальные, рюкзаки представляют собой трудную задачу - быстрого алгоритма для них не найдено. Единственным известным способом определить, какие предметы кладутся в рюкзак, является методическая проверка возможных решений, пока вы не наткнетесь на правильное . Самый быстрый алгоритм, принимая во внимание различную эвристику, имеет экспоненциальную зависимость от числа возможных предметов. Если добавить к последовательности весов еще один член, то найти решение станет вдвое труднее. Это намного труднее сверхвозрастающего рюкзака, где, если вы добавите один предмет к последовательности, поиск решения увеличится на одну операцию.
Алгоритм Меркла-Хеллмана основан на этом свойстве. Закрытый ключ является последовательностью весов проблемы сверхвозрастающего рюкзака. Открытый ключ - это последовательность весов проблемы нормального рюкзака с тем же решением. Меркл и Хеллман, используя модульную арифметику, разработали способ преобразования проблемы сверхвозрастающего рюкзака в проблему нормального рюкзака.
8.4.2 Создание открытого ключа из закрытого
Рассмотрим работу алгоритма. Чтобы получить нормальную последовательность рюкзака, возьмем сверхвозрастающую последовательность рюкзака, например, {2,3,6,13,27,52}, и умножим по модулю  все значения на число
все значения на число  . Значение модуля должно быть больше суммы всех чисел последовательности, например, 105. Множитель должен быть взаимно простым числом с модулем, например, 31. Нормальной последовательностью рюкзака будет
. Значение модуля должно быть больше суммы всех чисел последовательности, например, 105. Множитель должен быть взаимно простым числом с модулем, например, 31. Нормальной последовательностью рюкзака будет
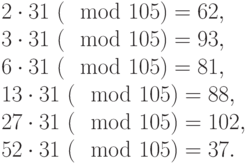
Итого - {62,93,81,88,102,37}.
Сверхвозрастающая последовательность рюкзака является закрытым ключом, а нормальная последовательность рюкзака - открытым.
8.4.3 Шифрование
Для шифрования сообщение сначала разбивается на блоки, равные по длине числу элементов последовательности рюкзака. Затем, считая, что единица указывает на присутствие члена последовательности, а ноль - на его отсутствие, вычисляем полные веса рюкзаков - по одному для каждого блока сообщения.
Например, если сообщение в бинарном виде выглядит как 011000110101101110, шифрование, использующее предыдущую последовательность рюкзака, будет происходить следующим образом:
- сообщение = 011000 110101 101110.
- 011000 соответствует
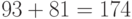 .
. - 110101 соответствует
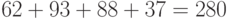 .
. - 101110 соответствует
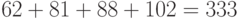 .
.
Шифртекстом будет последовательность 174,280,333.
8.3.4 Расшифрование
Законный получатель данного сообщения знает закрытый ключ: оригинальную сверхвозрастающую последовательность, а также значения  и
и  , использованные для превращения ее в нормальную последовательность рюкзака. Для расшифрирования сообщения получатель должен сначала определить обратный к
, использованные для превращения ее в нормальную последовательность рюкзака. Для расшифрирования сообщения получатель должен сначала определить обратный к  по модулю
по модулю  . Каждое значение щифротекста умножается на
. Каждое значение щифротекста умножается на  , а затем разделяется с помощью закрытого ключа, чтобы получить значения открытого текста.
, а затем разделяется с помощью закрытого ключа, чтобы получить значения открытого текста.
Для расшифрования используется выбранная ранее сверхвозрастающая последовательность {2, 3, 6, 13, 27, 52} с 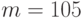 ,
,  . Шифртекстом служит 174,280,333. В этом случае
. Шифртекстом служит 174,280,333. В этом случае 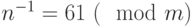 , поэтому значения шифртекста должны быть умножены на 61 по модулю 105.
, поэтому значения шифртекста должны быть умножены на 61 по модулю 105.
-
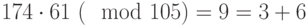 , что соответствует 011000
, что соответствует 011000 -
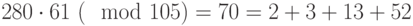 , что соответствует 110101
, что соответствует 110101 -
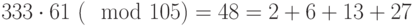 , что соответствует 101110
, что соответствует 101110
Расшифрованным открытым текстом является 011000 110101 101110.
8.4.5 Практические реализации
Для последовательности из шести элементов нетрудно решить задачу рюкзака, даже если последовательность не является сверхвозрастающей. Реальные рюкзаки должны содержать не менее 250 элементов. Длина каждого члена сверхвозрастающей последовательности должна быть где-то между 200 и 400 битами, а длина модуля должна быть от 100 до 200 битов. Для получения этих значений практические реализации используют генераторы псевдослучайной последовательности.
