|
как начать заново проходить курс, если уже пройдено несколько лекций со сданными тестами? |
Алгоритмы с открытыми ключами
8.3 Примеры атак на алгоритм RSA с большими числами
Приведем примеры атак с числами, размеры которых соответствуют реально применяем в системах защиты банковской информации.
Для работы с большими числами мы будем использовать систему компьютерной алгебры Maxima (см. параграф 1.16.1). Используемые нами функции подробно описаны в руководстве пользователя. Особенно полезен нам раздел "Number Theory".
8.3.1 Пример проведения атаки методом Ферма
Исходные данные:
 = 6915244609579137267327382519799379091524149293244816637691826
9398622964367867570234227167749609782487603063343406242777371955314645
2742388332988733993605091994058293499382971742490952474719828474075078
5896707348622744531600003265917743044563775026361237516233569510776114
8109796496185649768169137389070008752782413652613114179194481058554254
4448615819662193369744739530133016244020607483919296703035335756025782
1198618093610413148915963990789275952977743453275495105952399715239534
1404522821690462029654934969262380866920267097617165707930262759302606
756755216795383122881029602333988711966716180750531605801919527461
= 6915244609579137267327382519799379091524149293244816637691826
9398622964367867570234227167749609782487603063343406242777371955314645
2742388332988733993605091994058293499382971742490952474719828474075078
5896707348622744531600003265917743044563775026361237516233569510776114
8109796496185649768169137389070008752782413652613114179194481058554254
4448615819662193369744739530133016244020607483919296703035335756025782
1198618093610413148915963990789275952977743453275495105952399715239534
1404522821690462029654934969262380866920267097617165707930262759302606
756755216795383122881029602333988711966716180750531605801919527461
 =7423489;
=7423489;
шифртекст 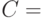 465060673245728679820089043475674731352115350813536
29127993992486567556 7156900806763889151763924735496714794491888355277
38596815041010164916640784130 4910760438532601276748143258914433560279
13186272146910522595250621775809097843 8466376070439866602619174245254
91796789390336635629378578035857597525297590776 2618424271931719171731
88933063050921552961787237676274649516864417659967226409 6655987478676
94982197189302733688441148495741687268763633927764999172932586878 6575
5502667348346941062611020674418896448890646803651538990666737332006313
6883 39309056851281655672233726633413389794443264266190435226307846633
6457114523067
465060673245728679820089043475674731352115350813536
29127993992486567556 7156900806763889151763924735496714794491888355277
38596815041010164916640784130 4910760438532601276748143258914433560279
13186272146910522595250621775809097843 8466376070439866602619174245254
91796789390336635629378578035857597525297590776 2618424271931719171731
88933063050921552961787237676274649516864417659967226409 6655987478676
94982197189302733688441148495741687268763633927764999172932586878 6575
5502667348346941062611020674418896448890646803651538990666737332006313
6883 39309056851281655672233726633413389794443264266190435226307846633
6457114523067
-
Запустим систему Maxima. После появления приглашения командной строки (%i1) можно вводить команды.
- Введём в систему входные данные. Для этого после идентификатора нужно поставить двоеточие, а затем значение. Каждая команда заканчивается символом ";" или "$". Символ "$" обозначает, что результат вычислений не нужно выводить на экран. Например, для ввода в систему числа
 введём:
введём:
e:7423489$После нажатия Enter происходит выполнение команды. Аналогичным образом введём идентификаторы
 ,
,  .
. - Проверим, что число
 не является квадратом. Для вычисления числа
не является квадратом. Для вычисления числа  для целого
для целого  используется команда isqrt. Для возведения в квадрат используется операция ^. Введём:
Первая команда вычисляет целую часть корня от
используется команда isqrt. Для возведения в квадрат используется операция ^. Введём:
Первая команда вычисляет целую часть корня отsrn:isqrt(N)$ is(srn^2=N); и обозначает её идентификатором srn. Вторая команда проверяет, является ли
и обозначает её идентификатором srn. Вторая команда проверяет, является ли  квадратом. В результате второй команды получим вывод:
квадратом. В результате второй команды получим вывод:
(%o5) falseЭто говорит о том, что равенство
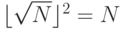 не выполняется, и число
не выполняется, и число  - не квадрат целого числа. Надпись "\verb#(%05)#" обозначает, что далее идёт результат 5-й команды, которая была введена после приглашения "\verb#(%i5)#".
- не квадрат целого числа. Надпись "\verb#(%05)#" обозначает, что далее идёт результат 5-й команды, которая была введена после приглашения "\verb#(%i5)#". - Для каждого числа
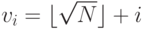 будем расчитывать
будем расчитывать  и проверять, является ли
и проверять, является ли 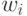 квадратом. Доллар вместо точки с запятой в конце выражения говорит системе не выводить на экран результаты промежуточных вычислений.
квадратом. Доллар вместо точки с запятой в конце выражения говорит системе не выводить на экран результаты промежуточных вычислений.
(%i6) w1 : (srn+1)^2 - N$ (%i7) is(isqrt(w1)^2=w1); (%o7) false (%i8) w2 : (srn+2)^2 - N$ (%i9) is(isqrt(w2)^2=w2); (%o9) false (%i10) w3 : (srn+3)^2 - N$ (%i11) is(isqrt(w3)^2=w3); (%o11) false (%i12) w4 : (srn+4)^2 - N$ (%i13) is(isqrt(w4)^2=w4); (%o13) trueИтак,
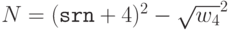 .
. - Теперь можно найти делители числа
 :
Проверим, правильно ли мы нашли делители:
:
Проверим, правильно ли мы нашли делители:(%i14) p:srn+4-isqrt(w4); (%o14) 262968526816026736232636051189459874382446519148 963617629027255104769945719755984982102707120117 706525064015257076350250162229292374187259939548 939791858838514297011479606873615542587565445952 774014851457711890959298629102287714458214768091 456036071496351940116236181014737608169537866387 475270200449701600539 (%i15) q:srn+4+isqrt(w4); (%015) 262968526816026736232636051189459874382446519148 963617629027255104769945719755984982102707120117 706525064015257076350250162229292374187259939548 939791858918434644001891354485948817612831393943 831874217795402559116173347849761999726607005334 107474067053693923414485042904885419841498167834 826934556836972951999(%i16) is(N=p*q); (%o16) trueТеперь нетрудно осуществить дешифровку.
- Найдём
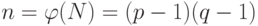 :
:
(%i17) n:(p-1)*(q-1); (%o17) 691524460957913726732738251979937909152414929324 481663769182693986229643678675702342271677496097 824876030633434062427773719553146452742388332988 733993605091994058293499382971742490952474719828 474075078589670734862274453160000326591774304456 377502636123751623356951077611481097964961856497 681691373890700087522564765989810607067292089561 753346960966889279214097392158985030920845106212 364219654648892933401895280839556667834036311647 010551595182396506795549490371941105829837814339 818401626212936221330490459000092664168447951206 651159937454409858770432466166667495195921598056 82710960700930681958448326848515244974924 - Найдём обратный к
 по модулю
по модулю  . Для нахождения обратного по модулю числа используется функция inv_mod.
. Для нахождения обратного по модулю числа используется функция inv_mod.
(%i18) d:inv_mod(e,n); (%o16) 159473778881412178951363380047548370299185595369 293301556900463792194735837486992335590486755090 118784764988909430054104623893214000053083933271 592133656057039185769018422628707296349955436619 729220378775558752251642918675436409902022493957 029259927562211781124457194260217400235337672814 214944366331695859094533195686344563818416832875 322618995339315686613690403531225496361587681392 769069101695698479902470067182274377952892405921 601214570482225781950523126294764189240377630662 614360117188441324480392776069704371618231484929 589094831167041492978941304862403054017212391664 53872109949533807664476342715222105274029 - Выполним дешифровку. Для возведения в степень по модулю нужно использовать функцию power_mod.
(%i19) P:power_mod(C,d,N); (%o19) 20231718 - Используя таблицу 6.1 (см. "лекцию 6" ), переведём число в текст: "КМЗИ".
8.3.2 Пример выполнения атаки "бесключевое чтение"
Исходные~данные:
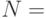 2519590847565789349402718324004839857142928212620403202777713
7836043662020707595556264018525880784406918290641249515082189298559149
1761845028084891200728449926873928072877767359714183472702618963750149
7182469116507761337985909570009733045974880842840179742910064245869181
7195118746121515172654632282216869987549182422433637259085141865462043
5767984233871847744479207399342365848238242811981638150106748104516603
7730605620161967625613384414360383390441495263443219011465754445417842
4020924616515723350778707749817125772467962926386356373289912154831438
167899885040445364023527381951378636564391212010397122822120720357;
2519590847565789349402718324004839857142928212620403202777713
7836043662020707595556264018525880784406918290641249515082189298559149
1761845028084891200728449926873928072877767359714183472702618963750149
7182469116507761337985909570009733045974880842840179742910064245869181
7195118746121515172654632282216869987549182422433637259085141865462043
5767984233871847744479207399342365848238242811981638150106748104516603
7730605620161967625613384414360383390441495263443219011465754445417842
4020924616515723350778707749817125772467962926386356373289912154831438
167899885040445364023527381951378636564391212010397122822120720357;
 ;
; 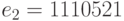 ;
;
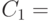 1475325512646127242922491234336573821326644830122724857802651
82834500418 6248451852916071172167393901484963211012186813420799457345
60638901218485778028 8088167762693301487173478582573846232471858233011
05429274234279863037579651294 1305440048424158412512493520129752032822
49047843226000864924203675006878533759 4689790689579026501643817929120
04105626763672704672827848013136399268699306662 7592945775958095422456
50919791860840020082746913903995338683355323748300077852 4222905192914
54785850041002811165491890932478197036280409606904111958813351896 3410
8240519966700126623731566589570806848893829480888979012581343525399802
490
1475325512646127242922491234336573821326644830122724857802651
82834500418 6248451852916071172167393901484963211012186813420799457345
60638901218485778028 8088167762693301487173478582573846232471858233011
05429274234279863037579651294 1305440048424158412512493520129752032822
49047843226000864924203675006878533759 4689790689579026501643817929120
04105626763672704672827848013136399268699306662 7592945775958095422456
50919791860840020082746913903995338683355323748300077852 4222905192914
54785850041002811165491890932478197036280409606904111958813351896 3410
8240519966700126623731566589570806848893829480888979012581343525399802
490
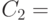 1168960834050268961897324310220295239101276316289170220279034
24838605267 3641103792818084219415738429514299664733141986982322386646
78264765952517495919 5383277543494845172200901017398976983581548883677
72471406710688871011254842119 0717106834141930230321678867355741169178
64117261510578555710832001442414172654 4343094430367130161092842091138
95716177545680184852854836102034397952992257055 3742268402669724738982
06540435293792709985777111719850811784302488645684794421 4372490969359
76159712998481145184343878513509137590163314701862659532716478010 6260
3880245750910942198158465793549050643147723479955672632110054161976725
720
1168960834050268961897324310220295239101276316289170220279034
24838605267 3641103792818084219415738429514299664733141986982322386646
78264765952517495919 5383277543494845172200901017398976983581548883677
72471406710688871011254842119 0717106834141930230321678867355741169178
64117261510578555710832001442414172654 4343094430367130161092842091138
95716177545680184852854836102034397952992257055 3742268402669724738982
06540435293792709985777111719850811784302488645684794421 4372490969359
76159712998481145184343878513509137590163314701862659532716478010 6260
3880245750910942198158465793549050643147723479955672632110054161976725
720
-
Запустим системы компьютерной алгебры Maxima и введём в неё исходные данные (подробнее см. предыдущий пример).
- Найдём наибольший общий делитель
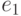 и
и 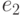 и коэффициенты его линейного представления. Для этого необходим пакет extgcd.
и коэффициенты его линейного представления. Для этого необходим пакет extgcd.
(%i6) [u1,u2,v]:igcdex(e1,e2); (%o6) [- 185750, 169131, 1] - Теперь, когда
 , найдём
, найдём  . Для этого используем функцию возведения в степень по модулю power_mod, которая при возведении в отрицательную степень автоматически находит элемент, обратный по модулю:
. Для этого используем функцию возведения в степень по модулю power_mod, которая при возведении в отрицательную степень автоматически находит элемент, обратный по модулю:
(%i7) m:mod(power_mod(c1,u1,N) * power_mod(c2,u2,N),N); (%o7) 17109930102028242618171032184099141023232413249933 18272110992310172310331523109923101326101410991299 14121527281899283727413399142421211926241299273410
Теперь, используя таблицу 6.1 (см. "лекцию 6" ), нетрудно прочитать зашифрованный текст:
ЗА ФАКТОРИЗАЦИЮ ДАННОГО ЧИСЛА НАЗНАЧЕНА НАГРАДА В ДВЕСТИ ТЫСЯЧ ДОЛЛАРОВ США
Действительно, за разложение на множители данного модуля положена награда в 200~000 долларов США. Маловероятно, что такая награда была бы назначена, если бы операция факторизации чисел такого размера была бы легкой задачей. Приведенный пример показывает, что криптосистема хоть и была построена на основе числа, надежность которого оценивается столь большой суммой, из-за неверной реализации и нарушения правил безопасного использования алгоритма RSA была проведена успешная атака на такую систему.
