|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Сбалансированные деревья
RB-деревья
Описанный в предыдущем разделе алгоритм вставки в нисходящие 2-3-4-деревья прост для понимания, но непосредственно его реализовать неудобно из-за того, что нужно рассматривать множество различных случаев. Чтобы сравнивать ключи поиска с каждым из ключей в узлах, копировать ссылки и другую информацию из одного типа узлов в другой, создавать и удалять узлы и т.д., приходится работать с тремя различными типами узлов. В этом разделе мы исследуем простое абстрактное представление 2-3-4-деревьев, которое позволяет создавать естественную реализацию алгоритмов таблиц символов с почти оптимальной гарантированной производительностью в худшем случае.
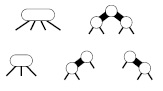
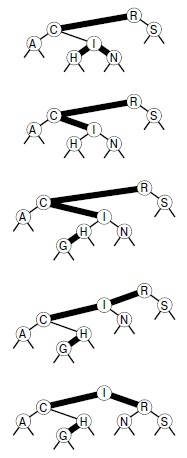
Основная идея заключается в представлении 2-3-4-деревьев в виде стандартных BST-деревьев (содержащих только 2-узлы), но с добавлением в каждом узле дополнительного информационного бита для кодирования 3-узлов и 4-узлов. Мы будем считать, что ссылки могут быть двух различных типов: красные ссылки (R-ссылки), которые объединяют небольшие бинарные деревья, образующие 3-узлы и 4-узлы, и черные ссылки (B-ссылки), которые объединяют 2-3-4-дерево. А именно, как показано на рис. 13.15, 4-узлы представляются тремя 2-узлами, соединенными R-ссылками, а 3-узлы — двумя 2-узлами, соединенными одной R-ссылкой. R-ссылка в 3-узле может быть левой или правой, следовательно, каждый 3-узел может быть представлен двумя способами.
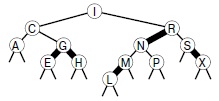
В любом дереве на каждый узел указывает одна ссылка, значит, окрашивание ссылок эквивалентно окрашиванию узлов. Поэтому мы используем по одному дополнительному разряду в каждом узле для хранения цвета ссылки, указывающей на этот узел. 2-3-4-деревья, представленные таким образом, называются красно-черными (или RB-) деревьями бинарного поиска. Ориентация каждого 3-узла определяется динамикой алгоритма, который будет описан ниже. Можно было бы выдвинуть правило, чтобы все 3-узлы были ориентированы одинаково, но это ни к чему. Пример RB-дерева показан на рис. 13.16. Если в нем исключить R-ссылки и свернуть соединяемые ими узлы, в результате получится 2-3-4-дерево, показанное на рис. 13.10.
RB-деревья обладают двумя важными свойствами: (1) стандартный метод найти для BST-деревьев работает без всяких изменений; (2) существует прямое соответствие между RB-деревьями и 2-3-4-деревьями, поэтому, используя и сохраняя это соответствие, можно реализовать алгоритм обработки сбалансированного 2-3-4-дерева. Мы возьмем лучшее из обоих подходов: простой метод поиска по стандартному BST-дереву и простой метод вставки-балансировки в 2-3-4-дереве поиска.
Использование двух типов связей обеспечивает эффективный способ представления 3-узлов и 4-узлов в 2-3-4-деревьях. Красные ссылки (жирные линии на схемах) используются для представления внутренних соединений в узлах, а черные ссылки (тонкие линии на схемах) — для представления связей 2-3-4-дерева. 4-узел (вверху слева) представляется сбалансированным поддеревом, состоящим из трех 2-узлов, которые соединены красными ссылками (вверху справа). Оба представления содержат три ключа и четыре черных ссылки. 3-узел (внизу слева) представляется одним 2-узлом, связанным с другим 2-узлом (слева или справа) единственной красной ссылкой (внизу справа). Оба представления содержат два ключа и три черных ссылки.
Метод поиска не проверяет поле, представляющее цвет узла, поэтому механизм балансировки не увеличивает время выполнения основной процедуры поиска. Каждый ключ вставляется только один раз, но в типичном приложении его поиск может выполняться многократно, поэтому общее время поиска сокращается (поскольку деревья сбалансированы) за счет сравнительно небольших затрат (т.к. во время поиска балансировка не выполняется). Невелики и дополнительные затраты, связанные со вставкой: действия по балансировке нужно выполнять только при обнаружении 4-узлов, а в дереве их количество невелико, поскольку они всегда разбиваются. Внутренним циклом процедуры вставки является код продвижения вниз по дереву (как и для операций вставки или поиска-вставки в стандартных BST-деревьях), с добавлением одной дополнительной проверки: если узел имеет два дочерних R-узла, он является частью 4-узла. Столь небольшие дополнительные затраты — основной фактор, определяющий эффективность RB-деревьев бинарного поиска.
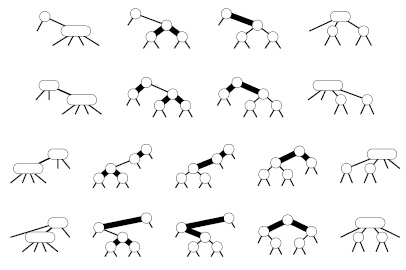
Рассмотрим теперь RB-представление двух преобразований, выполнение которых может потребоваться при обнаружении 4-узла. 2-узел с дочерним 4-узлом становится 3-узлом с двумя дочерними 2-узлами, а 3-узел с дочерним 4-узлом становится 4-узлом с двумя дочерними 2-узлами. Когда в нижнюю часть дерева добавляется новый узел, его можно представить в виде 4-узла, который должен быть разбит с передачей среднего узла вверх для вставки в тот нижний узел, в котором завершился поиск — нисходящий процесс гарантирует, что это либо 2-узел, либо 3-узел. Преобразование, требуемое при обнаружении 2-узла с дочерним 4-узлом, выполняется без труда, и такое же преобразование работает применительно к 3-узлу, " правильно " присоединенному к 4-узлу, как показано в двух первых примерах на рис. 13.17.
Остаются еще две ситуации, которые могут возникнуть при обнаружении 3-узла с дочерним 4-узлом — они показаны в последних двух примерах на рис. 13.17 рис. 13.17. (На самом деле существует четыре таких ситуации, поскольку другая ориентация 3-узлов может дать еще два зеркальных изображения.) В этих случаях простое разбиение 4-узла приводит к образованию двух последовательных R-ссылок, т.е. результирующее дерево не является 2-3-4-деревом в соответствии с принятыми соглашениями. Эта ситуация не так уж плоха, поскольку имеются три узла, соединенных R-ссылками: достаточно преобразовать дерево так, чтобы R-ссылки исходили из одного и того же узла.
К счастью, уже знакомые нам операции ротации — именно то, что необходимо для достижения требуемого эффекта. Начнем с более простого из двух оставшихся случаев — третьего примера на рис. 13.17, где 4-узел, присоединенный к 3-узлу, разбивается с порождением двух идущих друг за другом одинаково ориентированных R-ссылок. Эта ситуация не возникла бы, если бы 3-узел был ориентирован по-другому — значит, нужно изменить структуру дерева, переключив ориентацию 3-узла и сведя тем самым этот случай ко второму, когда достаточно простого разбиения 4-узла. Изменение структуры дерева для переориентации 3-узла достигается выполнением единственной ротации с дополнительным требованием изменения цвета двух задействованных узлов. Осталось рассмотреть случай, когда 4-узел, соединенный с 3-узлом, разбивается и оставляет две идущие подряд R-ссылки, которые ориентированы по-разному. Выполнением ротации можно свести этот случай к случаю с одинаково ориентированными ссылками, который затем обрабатывается, как было описано выше. Это преобразование сводится к выполнению тех же операций, что и при выполнении двойных ротаций влево-вправо и вправо-влево, которые использовались в разделе 13.2 для скошенных BST-деревьев, хотя нужны кое-какие дополнительные действия для правильной переустановки цветов. Примеры операций вставки в RB-деревья приведены на рис. 13.18 и 13.19.
На этом рисунке изображено RB-дерево, содержащее ключи A S R C H I N G E X M P L. Ключ в таком дереве можно найти при помощи стандартного поиска в BST-деревьях. В этом дереве любой путь от корня до внешнего узла содержит три B-ссылки. Если свернуть узлы, соединенные R-ссылками, получится 2-3-4-дерево, показанное на рис. 13.10.
В RB-дереве операция разбиения 4-узла, который не имеет родителем 4-узел, изменяет цвета узлов дерева, образующих 4-узел с последующим возможным выполнением одной или двух ротаций. Если родительский узел является 2-узлом (верхний рисунок) или 3-узлом с подходящей ориентацией (второй сверху рисунок), ротации не требуются. Если 4-узел располагается на центральной ссылке 3-узла (нижний рисунок), необходима двойная ротация; иначе достаточно одиночной ротации (третий сверху рисунок).
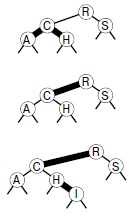
На этом рисунке показан результат (внизу) вставки записи с ключом I в RB-дерево (вверху). В этом случае процесс вставки состоит из разбиения 4-узла C с изменением цвета (в центре), последующим добавлением нового 2-узла в нижней части и преобразованием узла, содержащего ключ H, в 3-узел.
На этом рисунке показан результат (внизу) вставки записи с ключом G в RB-дерево (вверху). Для этого выполняется разбиение 4-узла с ключом I с изменением цвета (второй сверху рисунок), затем добавление нового узла в нижнюю часть (третий сверху рисунок) и, наконец, выполнение (с возвратом к каждому узлу на пути поиска после вызовов рекурсивных функций) ротации влево в узле C и ротации вправо в узле R, которые завершают процесс разбиения 4-узла.
Программа 13.6 является реализацией операции вставить для RB-деревьев, которая выполняет преобразования, приведенные на рис. 13.17. Рекурсивная реализация позволяет изменять цвета 4-узлов при продвижении вниз по дереву (перед рекурсивными вызовами), а затем выполнять ротации при продвижении вверх по дереву (после рекурсивных вызовов). Эту программу было бы трудно понять без двух уровней абстракции, разработанных для ее реализации. Несложно убедиться, что рекурсивный подход реализует ротации, изображенные на рис. 13.17; затем можно убедиться, что программа действительно реализует высокоуровневый алгоритм для 2-3-4-деревьев — разбивает 4-узлы при продвижении вниз по дереву, а затем вставляет новый элемент в 2- или 3-узел там, где путь поиска завершается в нижней части дерева.
Программа 13.6. Вставка в RB-деревья бинарного поиска
Данная функция реализует вставку в 2-3-4-деревья, используя их RB-представления. В тип node добавлен бит цвета red (и соответствующим образом расширен его конструктор): 1 означает, что узел красный, а 0 — черный. При продвижении вниз по дереву (перед рекурсивным вызовом) обнаруженные 4-узлы разбиваются путем изменения разрядов цвета во всех трех узлах. По достижении нижней части дерева для вставляемого элемента создается новый R-узел, и возвращается ссылка на него. При продвижении вверх по дереву (после рекурсивного вызова) проверяется, необходима ли ротация. Если путь поиска содержит две одинаково ориентированных R-ссылки, выполняется единственная ротация от верхнего узла, а затем разряды цвета изменяются так, чтобы получился правильный 4-узел. Если путь поиска содержит две по-разному ориентированных R-ссылки, выполняется единственная ротация от нижнего узла, в результате чего этот случай сводится к предыдущему, но уровнем выше.
private:
int red(link x)
{ if (x == 0) return 0; return x->red; }
void RBinsert(link& h, Item x, int sw)
{ if (h == 0)
{ h = new node(x); return; }
if (red(h->l) && red(h->r))
{ h->red = 1; h->l->red = 0; h->r->red = 0; }
if (x.key() < h->item.key())
{ RBinsert(h->l, x, 0);
if (red(h) && red(h->l) && sw) rotR(h);
if (red(h->l) && red(h->l->l))
{ rotR(h); h->red = 0; h->r->red = 1; }
}
else
{ RBinsert(h->r, x, 1);
if (red(h) && red(h->r) && !sw) rotL(h);
if (red(h->r) && red(h->r->r))
{ rotL(h); h->red = 0; h->l->red = 1; }
}
}
public:
void insert(Item x)
{ RBinsert(head, x, 0); head->red = 0; }
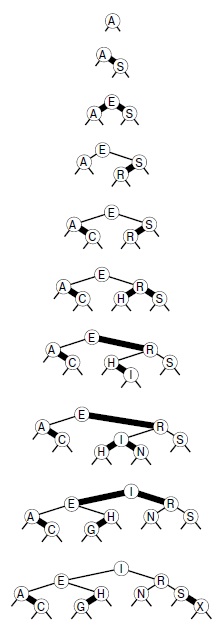
На рис. 13.20 рис. 13.20, который можно считать более подробной версией рис. 13.13, показано, как программа 13.6 строит RB-деревья, представляющие сбалансированные 2-3-4-деревья, с помощью вставки последовательности ключей. На рис. 13.21 изображено дерево, построенное для большей последовательности; среднее количество узлов, проверяемых во время поиска случайного ключа в этом дереве, равно лишь 5,81. Сравните это значение со значением 7,00 для дерева, построенного из этих же ключей в "Таблицы символов и деревья бинарного поиска" , и с 5,74 — наименьшим возможным для идеально сбалансированного дерева. Ценой лишь нескольких ротаций мы получаем дерево, сбалансированное гораздо лучше любого другого из приведенных в этой главе и состоящего из этих же ключей. Программа 13.6 — эффективный и сравнительно компактный алгоритм вставки, использующий структуру бинарного дерева, который гарантирует логарифмическое количество шагов для всех операций поиска и вставки. Это одна из немногих реализаций таблиц символов, обладающих подобным свойством, и ее стоит использовать в качестве библиотечной реализации, когда точно неизвестны свойства обрабатываемой последовательности ключей.
Здесь показана последовательность вставок записей с ключами A S E R C H I N X в первоначально пустое RB-дерево.
Лемма 13.8. Для поиска в RB-дереве с N узлами требуется менее 2lgN+2 сравнений.
Ротация в RB-дереве требуется только для разбиений, которые в 2-3-4-дереве соответствуют 3-узлу с последующим 4-узлом; таким образом, эта лемма — следствие леммы 13.2. Худший случай возникает тогда, когда путь к точке вставки состоит из чередующихся 3-узлов и 4-узлов. 
Кроме того, программа 13.6 выполняет очень немного действий, требуемых для балансировки, а создаваемые ей деревья почти оптимальны, поэтому ее стоит рассмотреть в качестве быстрого метода поиска общего назначения.
Лемма 13.9. Для поиска в RB-дереве с N узлами, построенном из случайных ключей, в среднем требуется около 1,002 lgN сравнений.
Константа 1,002, установленная с помощью частичного анализа и моделирования (см. раздел ссылок), достаточно мала, чтобы считать RB-деревья оптимальными для практического применения, но вопрос о том, действительно ли RB-деревья являются асимптотически оптимальными, остается открытым. Равна ли 1 эта константа в предельном случае? 
Поскольку в рекурсивной реализации программы 13.6 некоторые действия выполняются до рекурсивных вызовов, а некоторые — после них, ряд модификаций дерева выполняется при продвижении вниз, а ряд — на обратном пути вверх. Поэтому балансировка не выполняется в ходе лишь нисходящего прохождения. Это обстоятельство мало влияет на большинство приложений, поскольку глубина рекурсии гарантированно мала. Для некоторых приложений, связанных с несколькими независимыми процессами, которые обращаются к одному и тому же дереву, может потребоваться нерекурсивная реализация, которая в каждый момент времени активно оперирует только постоянным количеством узлов (см. упражнение 13.66).
Для приложения, которое хранит в дереве и другую информацию, операция ротации может оказаться дорогостоящей: возможно, придется обновлять информацию во всех узлах поддеревьев, затрагиваемых ротацией. Для таких приложений можно обеспечить, чтобы каждая вставка выполняла не более одной ротации, используя RB-деревья для реализации восходящих 2-3-4-деревьев поиска, которые описаны в конце раздела 13.3.
Это RB-дерево — результат вставки случайно упорядоченных ключей в первоначально пустое дерево. Для выполнения неудачных поисков в этом дереве требуется от 6 до 12 сравнений.
Вставка в эти деревья вызывает разбиение 4-узлов на пути поиска, которое требует изменений цвета, но не выполнения ротаций в RB-представлении, за которыми следует одна одиночная или двойная ротация (один из случаев, показанных на рис. 13.17), если первый 2-узел или 3-узел встречается выше на пути поиска (см. упражнение 13.59).
Если в дереве необходимо хранить повторяющиеся ключи, то, подобно тому, как это делалось в скошенных BST-деревьях, придется разрешить элементам с ключами, равными ключу данного узла, размещаться по обе стороны от него. В противном случае длинные последовательности повторяющихся ключей могут привести к серьезному дисбалансу. И вновь из этого наблюдения следует, что для отыскания всех элементов с данным ключом нужен специализированный код.
Как было сказано в конце раздела 13.3, RB-представления 2-3-4-деревьев входят в число нескольких схожих стратегий, которые были предложены для реализации сбалансированных бинарных деревьев (см. раздел ссылок). Как было показано, балансировка деревьев достигается операциями ротации: мы рассмотрели специфическое представление деревьев, которое упрощает принятие решения о моменте выполнения ротации. Другие представления деревьев ведут к другим алгоритмам, часть из которых мы сейчас кратко рассмотрим.
Старейшая и наиболее изученная структура данных для сбалансированных деревьев — сбалансированное по высоте, или AVL-дерево, исследованное Адельсоном-Вельским и Ландисом. Для этих деревьев характерно, что высоты двух поддеревьев каждого узла различаются максимум на 1. Если вставка приводит к тому, что высота одного из поддеревьев какого-либо узла увеличивается на 1, условие баланса может нарушиться. Однако в любом случае одна одиночная или двойная ротация восстановит баланс. Основанный на этом наблюдении алгоритм аналогичен методу восходящей балансировки 2-3-4-деревьев: выполняется рекурсивный поиск узла, затем, после рекурсивного вызова, выполняется проверка разбаланса и, при необходимости, одиночная или двойная ротация для восстановления баланса (см. упражнение 13.61). Для принятия решения о том, какие ротации нужно выполнять (если нужно), требуется знать, является ли высота каждого узла на 1 меньше, равна или на 1 больше высоты его родственного узла. Для прямого кодирования этой информации требуется по два бита на каждый узел, хотя, используя RB-абстракцию, можно обойтись и без дополнительной памяти (см. упражнения 13.62 и 13.65).
Поскольку 4-узлы не играют никакой специальной роли в алгоритме с использованием 2-3-4-деревьев, можно строить сбалансированные деревья по существу так же, но используя только 2-узлы и 3-узлы. Построенные таким образом деревья называются 2-3-деревьями; они были открыты Хопкрофтом (Hopcroft) в 1970 г. 2-3-деревья не обладают гибкостью, достаточной для построения удобного алгоритма нисходящей вставки. Кроме того, RB-структура может упростить реализацию, но восходящие 2-3-деревья не дают особых преимуществ по сравнению с восходящими 2-3-4-деревьями, поскольку для поддержания баланса по-прежнему требуются одиночные и двойные ротации. Восходящие 2-3-4-деревья несколько лучше сбалансированы и обладают тем преимуществом, что для каждой вставки требуется максимум одна ротация.
В "Внешний поиск" будет рассмотрен еще один важный тип сбалансированных деревьев — расширение 2-3-4-деревьев, называемое B-деревьями. B-деревья допускают существование до M ключей в одном узле для больших значений M и широко используются в приложениях поиска, работающих с очень большими файлами.
Мы уже определили RB-деревья их соответствием 2-3-4-деревьям. Интересно также сформулировать непосредственные структурные определения.
Определение 13.3. RB-дерево бинарного поиска — это дерево бинарного поиска, в котором каждый узел помечен как красный (R) либо черный (B), с наложением дополнительного ограничения, что никакие два красных узла не могут появляться друг за другом на любом пути от внешней ссылки до корня.
Определение 13.4. Сбалансированное RB-дерево бинарного поиска — это RB-дерево бинарного поиска, в котором все пути от внешних ссылок до корня содержат одинаковое количество черных узлов.
А теперь рассмотрим альтернативный подход к разработке алгоритма с использованием сбалансированного дерева. В нем полностью игнорируется абстракция 2-3-4-дерева и формулируется алгоритм вставки, который сохраняет основное свойство сбалансированных RB-деревьев бинарного поиска с помощью ротаций. Например, использование восходящего алгоритма соответствует присоединению нового узла в нижней части пути поиска с помощью R-ссылки, затем продвижению вверх по пути поиска с выполнением ротаций или изменений цвета, как это делалось в случаях, представленных на рис. 13.17, для разбиения любой встретившейся пары последовательных R-ссылок. Основные выполняемые при этом операции — те же, что и в программе 13.6 и в ее восходящем аналоге, но при этом имеются незначительные различия, поскольку 3-узлы могут быть ориентированы в любом направлении, операции могут выполняться в ином порядке и с равным успехом могут приниматься различные решения о выполнении ротаций.
Подведем итоги: используя RB-деревья для реализации сбалансированных 2-3-4-деревьев, можно разработать таблицу символов, в которой операция найти для ключа в файле, состоящем, скажем, из 1 миллиона элементов, может быть выполнена путем сравнения этого ключа приблизительно с 20 другими ключами. В худшем случае требуется не более 40 сравнений. Более того, с каждым сравнением связаны лишь небольшие накладные расходы, и поэтому быстрое выполнение операции найти гарантировано даже в очень больших файлах.
Упражнения
13.48. Нарисуйте RB-дерево бинарного поиска, образованное нисходящими вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево.
13.49. Нарисуйте RB-дерево бинарного поиска, образованное восходящими вставками элементов с ключами E A S Y Q U T I O N в указанном порядке в первоначально пустое дерево.
13.50. Нарисуйте RB-дерево, образованное в результате вставки по порядку латинских букв от A до K в первоначально пустое дерево, а затем опишите, что обычно происходит при построении дерева в процессе вставки возрастающей последовательности ключей.
13.51. Приведите последовательность вставок, в результате которой будет создано RB-дерево, изображенное на рис. 13.16.
13.52. Сгенерируйте два случайных RB-дерева с 32 узлами. Нарисуйте их (вручную или с помощью программы). Сравните их с (несбалансированными) BST-деревьями, построенными из этих же ключей.
13.53. Сколько различных RB-деревьев соответствуют 2-3-4-дереву, содержащему t3-узлов?
13.54. Нарисуйте все структурно различные RB-деревья поиска, содержащие N ключей, для 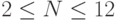 .
.
13.55. Для каждого из деревьев в упражнении 13.43 определите вероятность того, что оно является результатом вставки N случайных различных элементов в первоначально пустое дерево.
13.56. Составьте таблицу, в которой приведено количество деревьев для каждого значения N из упражнения 13.54, являющихся изоморфными в том смысле, что они могут быть преобразованы одно в другое путем обмена поддеревьев в узлах.
13.57. Покажите, что в RB-дереве, состоящем из N узлов, в худшем случае длина почти всех путей от корня к внешнему узлу равна 2lgN .
13.58. Сколько ротаций требуется в худшем случае для вставки в RB-дерево, состоящее из N узлов?
13.59. Используя RB-представление и тот же рекурсивный подход, что и в программе 13.6, реализуйте операции создать, найти и вставить для таблиц символов, основанных на использовании восходящих сбалансированных 2-3-4-деревьев. Совет: код может быть похож на программу 13.6, но должен выполнять операции в другом порядке.
13.60. Используя RB-представление и тот же рекурсивный подход, что и в программе 13.6, реализуйте операции создать, найти и вставить для таблиц символов, основанных на использовании восходящих сбалансированных 2-3-деревьев.
13.61. Используя тот же рекурсивный подход, что и в программе 13.6, реализуйте операции создать, найти и вставить для таблиц символов, основанных на использовании сбалансированных по высоте (AVL-) деревьев.
13.62. Измените реализацию из упражнения 13.61, чтобы использовать RB-деревья (содержащие по 1 биту на узел) для кодирования информации о балансе высоты.
13.63. Реализуйте сбалансированные 2-3-4-деревья, используя представление RB-дерева, в котором 3-узлы всегда наклонены вправо. Примечание: это изменение позволяет исключить из внутреннего цикла операции вставить одну битовую проверку.
13.64. Для сохранения сбалансированности 4-узлов программа 13.6 выполняет ротации. Разработайте использующую представление в виде RB-дерева реализацию сбалансированных 2-3-4-деревьев, в которой 4-узлы могут быть представлены любыми
тремя узлами, соединенными двумя R-ссылками (полностью сбалансированными или несбалансированными).
13.65. Не используя дополнительную память для хранения бита цвета, реализуйте для RB-деревьев операции создать, найти и вставить, воспользовавшись следующим приемом. Чтобы окрасить узел в красный цвет, поменяйте местами две его ссылки. А чтобы проверить, является ли узел красным, проверьте, больше ли его левый дочерний узел, чем правый. Для обеспечения возможного обмена ссылок придется модифицировать функции сравнения. Этот прием заменяет сравнения битов сравнениями ключей, что может потребовать больших затрат, однако он демонстрирует, что в случае необходимости можно избавиться от дополнительного поля в узлах.
13.66. Реализуйте нерекурсивную функцию вставки в RB-дерево бинарного поиска (см. программу 13.6), соответствующую вставке в сбалансированное 2-3-4-дерево за один проход. Совет: введите ссылки gg, g и p, которые указывают, соответственно, на прадеда, деда и родителя текущего узла в дереве. Все эти ссылки могут потребоваться для выполнения двойной ротации.
13.67. Напишите программу, которая вычисляет долю B-узлов в заданном RB-дереве бинарного поиска. Протестируйте программу, вставив N случайных ключей в первоначально пустое дерево, для N = 103, 104, 105 и 106 .
13.68. Напишите программу, которая вычисляет долю элементов, находящихся в 3-узлах и 4-узлах заданного 2-3-4-дерева поиска. Протестируйте программу, вставив N случайных ключей в первоначально пустое дерево, для N = 103, 104, 105 и 106 .
13.69. Используя по одному биту на узел для представления цвета, можно представлять 2-, 3- и 4-узлы. Сколько битов на узел потребовалось бы для представления бинарным деревом 5-, 6-, 7- и 8-узлов?
13.70. Эмпирически вычислите среднее значение и среднеквадратичное отклонение количества сравнений, используемых при успешном и неудачном поиске в RB-дереве, построенном вставками N случайных узлов в первоначально пустое дерево, для N = 103, 104, 105 и 106 .
13.71. Добавьте в программу из упражнения 13.70 возможность подсчета количества ротаций и разбиений узлов, используемых для построения деревьев. Проанализируйте полученные результаты.
13.72. Воспользуйтесь программой-драйвером из упражнения 12.30 для сравнения самоорганизующегося поиска в скошенных BST-деревьях с гарантированной производительностью, обеспечиваемой в худшем случае RB-деревьями бинарного поиска, и со стандартными BST-деревьями для распределений запросов на поиск, определенных в упражнениях 12.31 и 12.32 (см. упражнение 13.29).
13.73. Реализуйте функцию найти для RB-деревьев, которая выполняет ротации и изменяет цвета узлов при продвижении вниз по дереву, чтобы обеспечить, что узел в нижней части пути поиска не является 2-узлом.
13.74. Воспользуйтесь решением упражнения 13.73 для реализации функции удалить для RB-деревьев. Найдите узел, который должен быть удален, продолжите поиск до нахождения 3-узла или 4-узла в нижней части пути и переместите узел-наследник из нижней части, чтобы заменить удаленный узел.