Очереди с приоритетами и пирамидальная сортировка

Программа 9.14. Вставка в биномиальную очередь

Для вставки узла в биномиальную очередь его надо сначала преобразовать в 1-дерево и считать его 1-деревом переноса, а затем повторять в цикле следующий процесс, начиная с i = 0. Если в биномиальной очереди нет 2ⁱ-дерева, 2ⁱ переноса просто помещается в эту очередь. Если в биномиальной очереди такое дерево есть, оно объединяется с новым деревом (с помощью функции pair из программы 9.13), и получается 2ⁱ⁺¹ , после чего значение i увеличивается на 1, и процесс продолжается до обнаружения в биномиальной очереди пустой позиции.

  handle insert(Item v)
    { link t = new node(v), c = t;
      for (int i = 0; i < maxBQsize; i++)
        { if (c == 0) break;
        if (bq[i] == 0) { bq[i] = c; break; }
      c = pair(c, bq[i]); bq[i] = 0;
    }
    return t;
    }
        

Другие операции над биномиальными очередями также проще понять с помощью аналогии с операциями двоичной арифметики. Как мы вскоре убедимся, реализация операции объединить соответствует реализации операции сложения двоичных чисел.

Допустим, у нас есть (эффективный) способ выполнения операции объединить, предназначенный для слияния очереди с приоритетами, которая задана ссылкой во втором операнде функции, с очередью с приоритетами, которая задана ссылкой в первом операнде (результат помещается в первый операнд). С помощью этой функции операцию вставить можно реализовать, вызвав функцию объединить, в которой один из операндов представляет собой биномиальную очередь размера 1 (см. упражнение 9.63).

С помощью одного вызова операции объединить можно реализовать и операцию извлечь наибольший. Чтобы найти в биномиальной очереди максимальный элемент, нужно просмотреть деревья степени 2 в этой очереди. Каждое такое дерево является левосторонне пирамидально упорядоченным деревом, поэтому его максимальный элемент находится в корне. Больший из корневых элементов является наибольшим элементом биномиальной очереди. Поскольку в биномиальной очереди не может быть более lg N деревьев, общее время поиска наибольшего элемента меньше lg N.

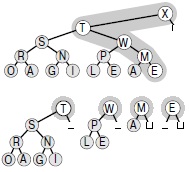
Для выполнения операции извлечь наибольший отметим, что удаление корня из левосторонне упорядоченного 2^k приводит к появлению к левосторонне упорядоченных деревьев степени 2 — 2^k-1 -дерево, 2^k-2 -дерево и т.д. — которые легко собрать в биномиальную очередь размера 2^k — 1 , как показано на рис. 9.18. Затем, чтобы завершить операцию извлечь наибольший, можно воспользоваться операцией объединить для объединения этой биномиальной очереди с остатком исходной очереди. Эта реализация приведена в программе 9.15.

Рис. 9.18. Удаление наибольшего элемента из пирамидального дерева степени 2

Удаление корня приводит к появлению леса деревьев степени 2; все они левосторонне пирамидально упорядочены, а их корни берутся из правого ствола дерева. Эта операция позволяет выполнить удаление наибольшего элемента из биномиальной очереди: убираем корень дерева степени 2, которое содержит наибольший элемент, затем выполняем операцию объединить для слияния полученной биномиальной очереди с остальными деревьями степени 2 исходной биномиальной очереди.

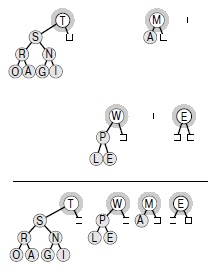
Каким образом объединяются две биномиальных очереди? Прежде всего заметим, что эта операция тривиальна, если в этих очередях нет деревьев степени 2 одинакового размера (см. рис. 9.19): мы просто сливаем пирамидальные деревья из обеих биномиальных очередей и получаем одну биномиальную очередь. Очередь размера 10 (состоящая из 8-дерева и 2-дерева) и очередь размера 5 (состоящая из 4-дерева и 1-дерева) путем простого слияния образуют очередь размера 15 (состоящую из 8-дерева, 4-дерева, 2-дерева и 1-дерева). Способ, рассчитанный на более общие случаи, основан на прямой аналогии с выполнением сложения с переносом двух двоичных чисел (см. рис. 9.20).

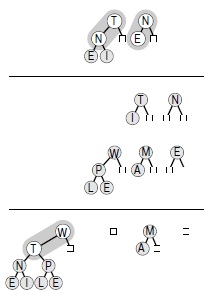
Например, если очередь размера 7 (состоящую из 4-дерева, 2-дерева и 1-дерева) добавить к очереди размера 3 (состоящую из 2-дерева и 1-дерева), получится очередь размером 10 (состоящая из 8-дерева и 2-дерева). Для такого добавления потребуется слить 1-деревья и выполнить перенос 2-дерева, затем слить 2-деревья и выполнить перенос 4-дерева, затем слить 4-деревья и получить в результате 8-дерево — точно так же, как выполняется двоичное сложение 011₂ + 111₂ = 1010₂ . Пример, представленный на рис. 9.19, проще примера на рис. 9.20, поскольку он аналогичен операции сложения без переносов 1010₂ + 0101₂ = 1111₂ .

Эта прямая аналогия с двоичной арифметикой приводит к естественной реализации операции объединить (см. программу 9.16). Для каждого разряда возможны восемь случаев, в зависимости от значений каждого из 3 разрядов (перенос и два разряда в операндах).

Программа 9.15. Извлечение наибольшего элемента из биномиальной очереди

Сначала производится просмотр корневых узлов для определения наибольшего, а затем из биномиальной очереди удаляется дерево степени 2, содержащее этот наибольший элемент. Далее корневой узел, содержащий наибольший элемент, удаляется из его дерева степени 2, и строится временная биномиальная очередь, содержащая остатки дерева степени 2. В завершение при помощи операции объединить выполняется слияние полученной и исходной биномиальных очередей.

  Item getmax()
    { int i, max; Item v = 0;
      link* temp = new link[maxBQsize];
      for (i = 0, max = -1; i < maxBQsize; i++)
        if (bq[i] != 0)
if ((max == -1) || (v < bq[i]->item))
  { max = i; v = bq[max]->item; }
      link x = bq[max]->l;
      for (i = max; i < maxBQsize; i++) temp[i] = 0;
      for ( i = max; i > 0; i-- )
        { temp[i-1] = x; x = x->r; temp[i-1]->r = 0; }
      delete bq[max]; bq[max] = 0;
      BQjoin (bq, temp);
      delete temp;
      return v;
    }
        

Рис. 9.19. Объединение двух биномиальных очередей (без переноса)

Если две объединяемые биномиальные очереди содержат только деревья степени 2 попарно различных размеров, то операция объединить сводится к простому слиянию. Выполнение этой операции аналогично сложению двух двоичных чисел, когда нет сложения битов 1 + 1 (т.е. без переносов). В рассматриваемом случае биномиальная очередь из 10 узлов сливается с очередью из 5 узлов, и в результате получается биномиальная очередь из 15 узлов, соответствующая операции 1010₂ + 0101₂ = 1111₂ .

Рис. 9.20. Объединение двух биномиальных очередей

В результате добавления биномиальной очереди из 3 узлов к биномиальной очереди из 7 узлов получается очередь из 10 узлов — аналогично операции сложения 011₂+111₂=1010₂ в двоичной арифметике. Добавление N к E дает пустое 1-дерево и 2-дерево переноса, содержащее узлы N и E. Последующее сложение трех 2-деревьев оставляет одно из них в итоговой очереди, а в перенос попадает 4-дерево с узлами T N E I. Это 4-дерево добавляется к другому 4-дереву, образуя биномиальную очередь, которая показана в нижней части диаграммы. В описанном процессе принимает участие лишь небольшое количество узлов.

Соответствующий код сложнее, чем для обычного сложения, поскольку в этом случае мы имеем дело с различными пирамидальными деревьями, а не с идентичными битами, но оба случая просты для понимания. Например, если все три разряда равны 1, нужно оставить одно дерево в результирующей биномиальной очереди, а два других объединить и перенести в следующую позицию. На самом деле эта операция предоставляет полный цикл на абстрактных типах данных: мы (с трудом) противимся искушению перевести программу 9.16 в статус полностью абстрактной двоичной процедуры сложения, после чего реализация биномиальной очереди окажется просто клиентской программой, использующей более сложную процедуру сложения битов из программы 9.13.

Программа 9.16. Объединение (слияние) двух биномиальных очередей

Данная программа имитирует операцию сложения двух двоичных чисел, продвигаясь справа налево с первоначально нулевым разрядом переноса. Здесь необходимо рассматривать восемь различных случаев (все возможные значения операндов и разряда переноса). Например, случай 3 соответствует тому, что биты обоих операндов равны 1, а бит переноса — 0. В этом случае результатом будет 0, а бит переноса становится равным 1 (в результате сложения разрядов операндов).

Как и функция pair, данная функция является приватной функцией-членом реализации, которая вызывается функциями getmax и join. Функция абстрактного типа данных join (PQ<Item>& p) реализована в виде вызова BQjoin(bq, p.bq).

  static inline int test(int C, int B, int A)
    { return 4*C + 2*B + 1*A; }
  static void BQjoin (link *a, link *b)
    { link c = 0;
      for (int i = 0; i < maxBQsize; i++)
        switch(test(c != 0; b[i] != 0, a[i] != 0))
        { case 2: a[i] = b[i]; break;
case 3: c = pair(a[i], b[i]); a[i] = 0; break;
case 4: a[i] = c, c = 0; break;
case 5: c = pair(c, a[i]); a[i] = 0; break;
case 6:
  case 7: c = pair(c, b[i]); break;
        }
    }
        

Как было сказано в разделе 4.8 "Абстрактные типы данных" , в реализации операции объединить в программе 9.16 не рассматривались вопросы распределения памяти. Из-за этого там имеется утечка памяти, так что в некоторых ситуациях она становится непригодной. Для исправления этого дефекта потребуется внимательно рассмотреть вопрос выделения памяти под аргументы и возвращаемое значение функции, которая реализует операцию объединить (см. упражнение 9.65).

Биномиальные очереди гарантируют высокое быстродействие, но все же были созданы структуры данных, теоретически обладающие еще лучшими характеристиками, которые гарантируют для некоторых операций постоянное время выполнения. Эта задача представляет собой интересную и активную отрасль разработки структур данных. Хотя практическая ценность многих из этих заумных структур сомнительна. Прежде чем пускаться на поиски решений среди сложных структур данных, ст ит убедиться, что действительно есть такие узкие места в производительности, от которых можно избавиться, только уменьшив время выполнения некоторых операций над очередями с приоритетами. Вообще-то в практических приложениях для отладки и небольших очередей лучше выбирать тривиальные структуры; а затем для ускорения операций нужно использовать пирамидальные деревья (если нет необходимости в быстрой операции объединить). Биномиальными очередями следует пользоваться, только если требуется гарантированное логарифмическое время выполнения всех операций. И все-таки пакет для работы с очередями с приоритетами на базе биномиальных очередей является ценным вкладом в библиотеку программного обеспечения.

Упражнения

9.54. Нарисуйте биномиальную очередь размера 29, используя представление биномиальным деревом.

9.55. Напишите программу построения графического представления биномиальной очереди в виде биномиального дерева с заданным размером N (только узлы, соединенные ребрами, без ключей).

9.56. Приведите биномиальную очередь, которая получится, если вставить ключи E A S Y Q U E S T I O N в первоначально пустую биномиальную очередь.

9.57. Приведите биномиальную очередь, которая получится, если вставить в первоначально пустую биномиальную очередь ключи E A S Y, и биномиальную очередь, которая получится, если вставить в первоначально пустую очередь ключи Q U E S T I O N. Затем выполните в обеих очередях операцию извлечь наибольший и приведите результат. И, наконец, покажите, что получится после применения к полученным очередям операции объединить.

9.58. Следуя соглашениям из упражнения 9.1, приведите последовательность биномиальных очередей, полученных в результате выполнения операций

P r I o 1 R * * I * T * Y * * * Q U E * * * U * E

в первоначально пустой биномиальной очереди.

9.59. Следуя соглашениям из упражнения 9.2, приведите последовательность биномиальных очередей, полученных в результате выполнения операций

( ( ( P R I O * ) + ( R * I T * Y * ) ) * * * ) + ( Q U E * * * U * E )

в первоначально пустой биномиальной очереди.

9.60. Докажите, что биномиальное дерево с 2ⁿ узлами имеет узлов на i-м уровне, для . (Отсюда и пошло название биномиальное дерево).

9.61. Разработайте такую реализацию биномиальной очереди, чтобы выполнялась лемма 9.7. Для этого внесите в тип данных биномиальной очереди размер этой очереди и используйте его для управления циклами.

9.62. Разработайте такую реализацию биномиальной очереди, чтобы выполнялась лемма 9.7. Для этого внесите в тип данных сигнальный указатель, отмечающий точку завершения циклов.

9.63. Реализуйте операцию вставить для биномиальных очередей с помощью явного использования только операции объединить.

9.64. Реализуйте операции изменить приоритет и извлечь для биномиальных очередей. Совет: Потребуется добавить в узлы третью ссылку, указывающую наверх.

9.65. Добавьте в реализации биномиальной очереди (программы 9.13—9.16) деструктор, конструктор копирования и перегруженную операцию присваивания, приведенные в тексте книги, чтобы получить АТД первого класса из упражнения 9.43. Напишите программу-драйвер для тестирования полученных интерфейса и реализации.

9.66. Сравните эмпирически биномиальные очереди и пирамидальные деревья в качестве инструмента для сортировки, как в программе 9.6, случайно упорядоченных ключей при N = 1000, 10⁴, 10⁵ и 10⁶ . Совет: см. упражнения 9.61 и 9.62.