|
Здравствуйте прошла курсы на тему Алгоритмы С++. Но не пришел сертификат и не доступен.Где и как можно его скаачат? |
Очереди с приоритетами и пирамидальная сортировка
Пирамидальная структура данных
Основной темой настоящей главы является простая структура данных, получившая название пирамидального дерева (heap), которая позволяет эффективно выполнять основные операции над очередями с приоритетами. Записи пирамидального дерева хранятся в массиве таким образом, что каждый ключ обязательно больше, чем значения ключей в двух других заданных позициях. В свою очередь, каждый из этих ключей должен быть больше, чем два других ключа и т.д. Такое упорядочение легко представить наглядно, если рассматривать эти ключи как входящие в бинарную древовидную структуру с ребрами, идущими от каждого ключа к двум меньшим его ключам.
Определение 9.2. Дерево называется пирамидально упорядоченным (heap-ordered), если ключ в каждом его узле больше или равен ключам всех дочерних узлов этого узла (если они есть). Эквивалентная формулировка: ключ в каждом узле пирамидально упорядоченного дерева меньше или равен ключу узла, который является родителем данного узла (если он есть).
Лемма 9.1. Никакой узел пирамидально упорядоченного дерева не может иметь ключ больший, чем ключ в корне дерева.
Ограничение пирамидальной упорядоченности можно наложить на любое дерево. Однако удобнее всего пользоваться полным бинарным деревом (complete binary tree). В
"Элементарные структуры данных"
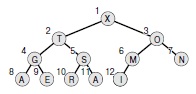
было показано, что такую структуру можно начертить, начав с корневого узла вверху страницы, а затем передвигаясь по странице вниз и слева направо, присоединяя к каждому узлу предыдущего уровня два узла текущего уровня до размещения всех N узлов. Полное бинарное дерево можно представить в виде массива, поместив корневой узел в позицию 1, его дочерние узлы в позиции 2 и 3, узлы следующего уровня в позиции 4, 5, 6 и 7 и т.д., как показано на
рис.
9.2. 
Определение 9.3. Пирамидальное дерево есть множество узлов с ключами, образующих полное пирамидально упорядоченное бинарное дерево, представленное в виде массива.
Можно было бы воспользоваться связным представлением пирамидально упорядоченных деревьев, но полные деревья предоставляют возможность использовать компактное представление в виде массива, в котором легко переходить от узла к его родителю или к дочерним узлам без необходимости хранения явных ссылок. Родитель узла в позиции i находится в позиции  и, соответственно, два потомка узла в позиции i находятся в позициях 2 i и 2 i + 1. При такой организации обход дерева выполняется проще, чем если бы это дерево было реализовано в связном представлении, поскольку тогда на каждый ключ понадобились бы три ссылки, чтобы иметь возможность перемещаться по дереву вверх и вниз (каждый элемент будет иметь один указатель на родителя и по одному указателю на оба дочерних узла). Полные бинарные деревья, представленные в виде массивов, являются жесткими структурами, но все же обладают достаточной гибкостью для реализации эффективных алгоритмов работы с очередями с приоритетами.
и, соответственно, два потомка узла в позиции i находятся в позициях 2 i и 2 i + 1. При такой организации обход дерева выполняется проще, чем если бы это дерево было реализовано в связном представлении, поскольку тогда на каждый ключ понадобились бы три ссылки, чтобы иметь возможность перемещаться по дереву вверх и вниз (каждый элемент будет иметь один указатель на родителя и по одному указателю на оба дочерних узла). Полные бинарные деревья, представленные в виде массивов, являются жесткими структурами, но все же обладают достаточной гибкостью для реализации эффективных алгоритмов работы с очередями с приоритетами.
В разделе 9.3 мы увидим, что пирамидальные деревья позволяют реализовать все операции над очередями с приоритетами (за исключением операции объединить) таким образом, что на свое выполнение они потребуют логарифмическое время в худшем случае. Все такие реализации оперируют узлами вдоль некоторого пути в пирамидальном дереве (от родителя вниз к дочерним узлам или от дочернего узла вверх к родителю, но без смены направления). Как было показано в "Элементарные структуры данных" , все пути в полном дереве, состоящем из N узлов, содержат порядка lg N узлов: примерно N/2 узлов находятся на самом нижнем уровне, N/4 узлов — узлы с дочерними узлами на нижнем уровне, N/8 узлов — " внуки " которых занимают нижний уровень и т.д. Каждое поколение узлов содержит приблизительно вдвое меньше узлов, чем последующее, а всего может быть максимум lg N поколений.
Ситуация, когда элемент в позиции 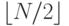 массива является родителем элемента в позиции i, для
массива является родителем элемента в позиции i, для  (или, что то же самое, когда i-й элемент является родителем 2 i -го и (2 i + 1)-го элементов), соответствует удобному представлению элементов массива в виде дерева.
(или, что то же самое, когда i-й элемент является родителем 2 i -го и (2 i + 1)-го элементов), соответствует удобному представлению элементов массива в виде дерева.
Это соответствие эквивалентно нумерации узлов полного бинарного дерева (с заполнением нижнего уровня слева) по уровням Дерево пирамидально упорядочено (heap-ordered), если ключ в любом узле больше или равен ключам его дочерних узлов. Пирамидальное дерево (heap) является представлением полного пирамидально упорядоченного бинарного дерева в виде массива. Его i-й элемент больше или равен и 2 i -му, и (2 i + 1)-му.
Для разработки эффективных реализаций операций над очередями с приоритетами можно также воспользоваться явными связными представлениями древовидных структур. В качестве примеров можно привести полные пирамидально упорядоченные деревья с тремя ссылками (см. раздел 9.5), турниры (см. программу 5.19) и биномиальные очереди (см. раздел 9.7). Как и в случае простых стеков и очередей, одна из главных причин, побуждающих рассматривать связные представления, заключается в том, что в этом случае нет необходимости заранее знать максимальный размер очереди, что требуется в случае представления в виде массива. В некоторых случаях гибкость, обеспечиваемая связными структурами, позволяет разработать эффективные алгоритмы. Читателям, которые не имеют достаточного опыта использования явных древовидных структур, прежде чем иметь дело со связными представлениями деревьев, рассматриваемых в упражнениях этой главы и в разделе 9.7, рекомендуется прочитать "Таблицы символов и деревья бинарного поиска" и ознакомиться с базовыми методами реализации еще более важных абстрактных типов данных — таблиц символов. Однако капитальное изучение связных структур можно оставить до второго чтения, поскольку основной темой настоящей главы является пирамидальное дерево (представление с помощью массива без ссылок в виде полного пирамидально упорядоченного дерева).
Упражнения
9.17. Является ли массив, отсортированный в нисходящем порядке, пирамидальным деревом?
9.18. Наибольший элемент пирамидального дерева должен находиться в позиции 1, а второй наибольший элемент должен занимать позицию 2 или 3. Приведите список позиций в пирамидальном дереве из 15 элементов, в которых к-й наибольший элемент (1) может появиться и (2) не может появиться, для к = 2, 3, 4 (значения всех элементов различны).
9.19. Выполните упражнение 9.18 для произвольного к как функции от N, представляющего собой размер пирамидального дерева.
9.20. Выполните упражнения 9.18 и 9.19 для к-го наименьшего элемента.
Алгоритмы на пирамидальных деревьях
Все алгоритмы очередей с приоритетами на основе пирамидальных деревьев работают таким образом: сначала вносится простое изменение, которое может нарушить структуру дерева, а затем выполняется обход дерева с такими изменениями, чтобы оно снова стало пирамидальным. Этот процесс иногда называют установлением пира-мидальности (heapifying) или просто восстановлением (fixing) пирамидального дерева. Возможны два случая. Если приоритет какого-либо узла увеличивается (или в нижний уровень пирамидального дерева добавляется новый узел), то чтобы восстановить структуру пирамидального дерева, нужно двигаться вверх по дереву. Если приоритет какого-либо узла уменьшается (например, при замене корневого узла новым узлом), то для восстановления структуры пирамидального дерева нужен проход вниз по дереву. Для начала мы обсудим, как реализовать эти две базовые функции, а затем подумаем, как с их помощью реализовать различные операции над очередями с приоритетами.
Если пирамидальность дерева нарушена из-за того, что ключ некоторого узла стал больше ключа родительского узла, можно попытаться исправить это нарушение, обменяв местами этот узел с его родителем. После обмена этот узел становится больше, чем оба его потомка (один из них — это прежний родитель, а другой меньше, чем старый родитель, поскольку он был потомком этого узла), но все еще может оставаться больше своего родителя. Это нарушение можно исправить аналогичным способом — продвигаясь далее вверх по дереву, пока не будет достигнут либо узел с большим ключом, либо корень. Пример описанного процесса показан на рис. 9.3. Код, реализующий его, примитивен, т.к. основан на том, что родитель узла, занимающего в пирамидальном дереве позицию k, находится в позиции k/2. Программа 9.3 является реализацией метода, который восстанавливает возможные нарушения из-за увеличения приоритета в некотором узле пирамидального дерева, продвигаясь вверх по дереву.
Если же пирамидальность дерева была нарушена из-за того, что ключ какого-либо узла стал меньше одного или обоих ключей его потомков, можно попытаться устранить это нарушение, обменяв узел с большим из его двух потомков. Такой обмен может вызвать нарушение пирамидальности дерева на узле-потомке; его можно устранить таким же способом и двигаться вниз по дереву до достижения либо узла, оба потомка которого меньше его самого, либо нижнего уровня дерева. Пример этого процесса показан на рис. 9.4. В коде опять используется тот факт, что потомки узла пирамидального дерева в позиции k находятся в позициях 2 k и 2k+1.
Программа 9.3. Восходящее восстановление пирамидальности
Чтобы восстановить пирамидальную структуру после повышения приоритета какого-либо узла, мы продвигаемся вверх по дереву, обменивая при необходимости узел в позиции k с его родителем (в позиции k/2), и продолжаем этот процесс, пока выполняется условие a[k/2] <a[k], или до достижения корня дерева.
template <class Item>
void fixUp(Item a[], int k)
{ while (k > 1 && a[k/2] < a[k])
{ exch (a[k], a[k/2]); k = k/2; }
}
Дерево, показанное вверху, пирамидально упорядочено, за исключением элемента T на нижнем уровне. Обмен T с его родительским узлом поправляет пирамидальный порядок — за исключением того, что теперь T может быть больше нового родителя. Обмен элемента T с его родителями продолжается до тех пор, пока не встретится корень или такой узел на пути от T к корню, который будет больше T — тогда будет восстановлена пирамидальность всего дерева. На основе этой процедуры можно построить операцию вставить: для этого нужно добавить в дерево новый элемент (справа на нижнем уровне или, если необходимо, на вновь созданном уровне), а потом восстановить пирамидальность.
Дерево, показанное вверху, пирамидально упорядочено, за исключением корня. Обмен элемента O с большим из его дочерних узлов (X) поправляет пирамидальный порядок, за исключением поддерева с корнем O. Обмен элемента O с большим из его дочерних узлов продолжается до достижения нижнего уровня дерева или момента, когда O будет больше обоих своих дочерних узлов — тогда будет восстановлена пирамидальность всего дерева. На основе этой процедуры можно построить операцию извлечь наибольший: для этого нужно заменить элемент в корне самым правым элементом на нижнем уровне, а потом восстановить пирамидальность.
Программа 9.4 является реализацией метода, который восстанавливает возможные нарушения из-за понижения приоритета некоторого узла пирамидального дерева, передвигаясь вниз по этому дереву. Этой функции должен быть известен размер пирамидального дерева (N), чтобы определить момент достижения нижнего уровня дерева.
Обе эти операции не зависят от способа представления структуры дерева, если возможен доступ к родительскому узлу (восходящий метод) и к дочерним узлам (нисходящий метод) любого узла. В восходящем методе мы перемещаемся вверх по дереву, обменивая ключ данного узла с ключом его родителя, пока не выйдем на корневой узел или на родителя с большим (или равным) ключом. В нисходящем методе мы перемещаемся вниз по дереву, обменивая ключ данного узла с большим из ключей его дочерних элементов и переходя к этому потомку, пока не будет достигнут нижний уровень или место, где нет потомков с большими ключами. В таком обобщенном виде эти операции применимы не только к бинарным деревьям, но и к любой древовидной структуре. Продвинутые алгоритмы обработки очередей с приоритетами обычно используют древовидные структуры более общего вида, но основаны на этих же базовых операциях, поддерживающих положение наибольшего ключа этой структуры в ее корне.
Если вообразить себе, что пирамидальное дерево представляет иерархию некой корпорации, в которой каждый дочерний узел представляет подчиненного (а каждый родитель — непосредственного начальника), то эти операции допускают забавную интерпретацию. Восходящий метод соответствуют появлению нового перспективного руководителя, который продвигается по служебной лестнице с одного поста на другой (обмениваясь должностями со всеми руководителями, имеющими более низкую квалификацию), до тех пор, пока этот новый работник не упрется в более квалифицированного босса. Нисходящий метод похож на ситуацию, когда президента компании сменяет на его посту другой, уступающий ему по квалификации. Если самый умелый из подчиненных президента квалифицированнее нового работника, они обмениваются должностями, и происходит спуск по служебной лестнице с понижением нового работника и повышением других, пока не будет достигнут уровень компетенции нового работника и не остается ни одного подчиненного, превосходящего его по квалификации (в реальной жизни этот идеализированный процесс наблюдается нечасто). Таким образом, движение вверх по пирамидальному дереву соответствует повышению, а вниз — понижению в должности.
Программа 9.4. Нисходящее восстановление пирамидальности
Чтобы восстановить пирамидальную структуру после понижения приоритета какого-либо узла, мы двигаемся вниз по дереву, обменивая при необходимости узел в позиции k с большим из двух его дочерних узлов, и останавливаемся, когда узел в позиции k не меньше обоих своих дочерних узлов или когда достигнут нижний уровень. Обратите внимание, что если N четно и k равно N/2, то у узла в позиции k только один дочерний узел — этот случай требует особого подхода!
У внутреннего цикла в этой программе два отдельных выхода: один для случая, когда достигнут нижний уровень, а другой для случая, когда условие пирамидальности выполняется где-то внутри дерева. Это характерный пример необходимости применения конструкции break.
template <class Item>
void fixDown(Item a[ ], int k, int N)
{ while (2*k <= N)
{ int j = 2*k;
if (j < N && a[j] < a[j + 1]) j++;
if (!(a[k] < a[j])) break;
exch (a[k], a[j]); k = j;
}
}
Эти две основные операции позволяют эффективно реализовать базовый АТД очереди с приоритетами — см. программу 9.5. Если очередь с приоритетами представлена как пирамидально упорядоченный массив, то операция вставить сводится к добавлению нового элемента в конец массива и перемещению этого элемента вверх по массиву для восстановления пирамидальности; а операция извлечь наибольший сводится к удалению наибольшего элемента из вершины дерева с последующей пересылкой элемента из конца дерева в его вершину и перемещением его вниз по массиву для восстановления пирамидальной структуры.
Лемма 9.2. Операции вставить и извлечь наибольший для абстрактного типа данных очереди с приоритетами могут быть реализованы с помощью пирамидально упорядоченных деревьев таким образом, что для очереди из N элементов операция вставить потребует не более lg N сравнений, а операция извлечь наибольший — не более 2 lg N сравнений.
Обе операции используют перемещение вдоль пути между корнем и нижним уровнем дерева, а ни один путь в пирамидальном дереве из N элементов не содержит более lg N элементов (см. например, лемму 5.8 и упражнение 5.77). Операция извлечь наибольший требует двух сравнений для каждого узла: одно для определения дочернего узла с большим ключом, другое — для принятия решения, нужно ли выполнять обмен с этим дочерним узлом.