Исчисление предикатов
93. Приведите пример формулы вида 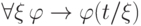 ,
в которой происходит коллизия переменных и которая не является
общезначимой. (Ответ:
,
в которой происходит коллизия переменных и которая не является
общезначимой. (Ответ: 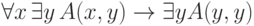 .)
.)
Поэтому нам придется принять еще одну меру предосторожности и
формально определить понятие корректной подстановки терма
вместо переменной. Мы будем говорить, что подстановка терма  вместо переменной
вместо переменной  корректна, если в процессе текстуальной
замены всех свободных вхождений переменной
корректна, если в процессе текстуальной
замены всех свободных вхождений переменной  на
терм
на
терм  никакая переменная из
никакая переменная из  не попадает в область действия
одноименного квантора.
не попадает в область действия
одноименного квантора.
Педантичный читатель мог бы попросить доказать, что результат такой подстановки будет формулой. Это проще всего сделать так: дать индуктивное определение корректной подстановки, равносильное исходному.
Сначала определим индуктивно результат подстановки терма  вместо переменной
вместо переменной  в терм
в терм  ; этот результат будем
обозначать
; этот результат будем
обозначать 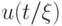 :
:
-
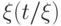 есть
есть  ; для любой
переменной
; для любой
переменной 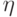 , отличной
от
, отличной
от  , мы полагаем
, мы полагаем 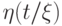 равным
равным 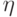 .
. - если
 есть
есть  - местный функциональный символ, а
- местный функциональный символ, а 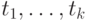 — термы, то
— термы, то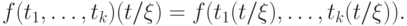
Теперь индуктивное определение продолжается для формул:
- для атомарных формул: если
 есть
есть  -местный предикатный символ, а
-местный предикатный символ, а 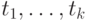 — термы, тои подстановка является корректной;
— термы, тои подстановка является корректной;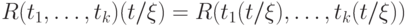
- подстановка терма
 вместо переменной
вместо переменной  в
формулу
в
формулу 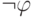 корректна, если она корректна для формулы
корректна, если она корректна для формулы  ,
при этом(квадратные скобки указывают порядок действий, не являясь частью формулы);
,
при этом(квадратные скобки указывают порядок действий, не являясь частью формулы);![[\lnot \varphi] (t/\xi) = \lnot [\varphi(t/\xi)]](/sites/default/files/tex_cache/8a47ac6e46d1d6967e64867798e5b331.png)
- подстановка терма
 вместо переменной
вместо переменной  в
формулу
в
формулу 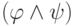 корректна, если она корректна для обеих
формул
корректна, если она корректна для обеих
формул  и
и  , при этоманалогично для формул
, при этоманалогично для формул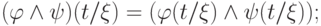
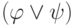 и
и  ;
; -
наконец, подстановка
 вместо
вместо  в формулу
в формулу 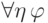 корректна в двух случаях:
корректна в двух случаях:(1) если
 не является параметром формулы
не является параметром формулы 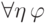 (это возможно, когда
(это возможно, когда  не является
параметром
не является
параметром  или когда
или когда  совпадает
с
совпадает
с 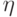 ); при этом подстановка ничего не меняет в формуле;
); при этом подстановка ничего не меняет в формуле;(2) переменная
 является параметром формулы
является параметром формулы 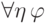 , но переменная
, но переменная 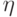 не входит в
терм
не входит в
терм  и подстановка
и подстановка 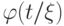 корректна; при этом
корректна; при этом![[\forall \eta \, \varphi] (t/\xi) = \forall \eta\,[\varphi (t/\xi)].](/sites/default/files/tex_cache/8872a07625b3a20c526cb751ffd0f05d.png)
Аналогично определяется корректная подстановка в формулу
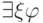 .
.
Главная часть в этом определении — последний его пункт, который,
во-первых, говорит, что вместо связанных вхождений переменных
ничего подставлять не надо, а во-вторых, требует, чтобы при корректной
подстановке переменные из терма  не подпадали под действие
одноименных кванторов.
не подпадали под действие
одноименных кванторов.
После всех этих приготовлений мы можем сформулировать две оставшиеся схемы аксиом исчисления предикатов: формула
(12) 
и двойственная ей формула
(13) 
будут аксиомами исчисления предикатов, если указанные в них подстановки корректны.
Два частных случая, когда подстановка заведомо корректна: во-первых, можно безопасно подставлять константу (или любой терм без параметров), во-вторых, подстановка переменной вместо себя всегда корректна (и ничего не меняет в формуле).
Отсюда следует, что формулы 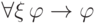 и
и 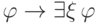 будут аксиомами исчисления
предикатов (для любой формулы
будут аксиомами исчисления
предикатов (для любой формулы  и переменной
и переменной  ).
).
Нужны ли нам еще какие-нибудь аксиомы и правила вывода?
Конечно, нужны, поскольку уже сформулированные аксиомы не
полностью отражают смысл кванторов. (Например, они вполне
согласуются с таким пониманием этого смысла: формула 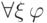 всегда ложна, а формула
всегда ложна, а формула 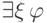 всегда истинна.) Поэтому мы введем в наше исчисление два правила
вывода, называемые правилами Бернайса,
и на этом определение исчисления предикатов будет завершено. (Позже мы
рассмотрим дополнительные аксиомы, отражающие специальный статус
предиката равенства.
всегда истинна.) Поэтому мы введем в наше исчисление два правила
вывода, называемые правилами Бернайса,
и на этом определение исчисления предикатов будет завершено. (Позже мы
рассмотрим дополнительные аксиомы, отражающие специальный статус
предиката равенства.
Если переменная  не является параметром
формулы
не является параметром
формулы  , то правила Бернайса разрешают такие переходы:
, то правила Бернайса разрешают такие переходы:

Поясним интуитивный смысл этих правил. Первое говорит, что если
из  следует
следует  , причем в
, причем в  есть
параметр
есть
параметр  , которого нет в
, которого нет в  , то это означает,
что формула
, то это означает,
что формула  истинна при всех значениях параметра
истинна при всех значениях параметра  , если только формула
, если только формула  истинна.
истинна.
Используя первое правило Бернайса, легко установить допустимость правила обобщения
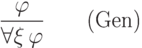
 без параметров (например,
аксиому, в которой вместо
без параметров (например,
аксиому, в которой вместо  ,
,  и
и  подставлены замкнутые формулы). Раз выводима формула
подставлены замкнутые формулы). Раз выводима формула  , то выводима
и формула
, то выводима
и формула  (поскольку
(поскольку  является тавтологией и даже аксиомой). Теперь по правилу Бернайса
выводим
является тавтологией и даже аксиомой). Теперь по правилу Бернайса
выводим 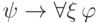 и применяем правило
MP к этой формуле и к формуле
и применяем правило
MP к этой формуле и к формуле  .
.Правило (Gen) (от Generalization — обобщение) кодифицирует
стандартную практику рассуждений: мы доказываем какое-то
утверждение  со свободной переменной
со свободной переменной  ,
после чего заключаем, что мы доказали
,
после чего заключаем, что мы доказали 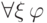 , так как
, так как  было произвольным.
было произвольным.
Второе правило Бернайса также вполне естественно: желая
доказать  в предположении
в предположении 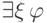 ,
мы говорим: пусть такое
,
мы говорим: пусть такое  существует, возьмем его
и докажем
существует, возьмем его
и докажем  (то есть докажем
(то есть докажем  со свободной переменной
со свободной переменной  ).
).
94. Покажите, что класс выводимых в исчислении предикатов формул не изменится, если мы вместо правил Бернайса добавим туда правило обобщения и две аксиомы


 не была параметром
формулы
не была параметром
формулы  ).
).Как и в случае исчисления высказываний, перед нами стоят две задачи: надо доказать корректность исчисления предикатов (всякая выводимая формула общезначима) и его полноту (всякая общезначимая формула выводима). Этим мы и займемся в следующих разделах.
