Выразимость в арифметике
Невыразимые предикаты: автоморфизмы
Мы видели, как можно доказать выразимость некоторых свойств. Сейчас мы покажем, каким образом можно доказывать невыразимость.
Начнем с такого примера. Пусть сигнатура содержит двуместный предикат равенства
(  ) и двуместную операцию сложения (
) и двуместную операцию сложения ( 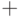 ). Рассмотрим ее
интерпретацию, носителем которой являются целые числа, а
равенство и сложение интерпретируются стандартным образом.
Оказывается, что предикат
). Рассмотрим ее
интерпретацию, носителем которой являются целые числа, а
равенство и сложение интерпретируются стандартным образом.
Оказывается, что предикат  не является выразимым.
не является выразимым.
Причина очевидна: с точки зрения сложения целые числа устроены
симметрично, положительные ничем не отличаются от отрицательных.
Если мы изменим знак у всех переменных, входящих в формулу, то
ее истинность не может измениться. Но при этом  заменится
на
заменится
на 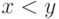 , и потому это свойство не является выразимым.
, и потому это свойство не является выразимым.
Формально говоря, надо доказывать по индукции такое свойство:
если формула  указанной сигнатуры
истинна при оценке
указанной сигнатуры
истинна при оценке  , то она истинна и
при оценке
, то она истинна и
при оценке 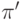 , в которой значения всех переменных меняют
знак. (Подробно мы объясним это в общей ситуации дальше.)
, в которой значения всех переменных меняют
знак. (Подробно мы объясним это в общей ситуации дальше.)
Сформулируем общую схему, которой следует это рассуждение. Пусть
имеется некоторая сигнатура  и интерпретация этой
сигнатуры, носителем которой является множество
и интерпретация этой
сигнатуры, носителем которой является множество  . Взаимно
однозначное отображение
. Взаимно
однозначное отображение 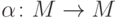 называется
автоморфизмом интерпретации, если все функции и
предикаты, входящие в интерпретацию, устойчивы относительно
называется
автоморфизмом интерпретации, если все функции и
предикаты, входящие в интерпретацию, устойчивы относительно  . При этом
. При этом  -местный предикат
-местный предикат  называется устойчивым относительно
называется устойчивым относительно  , если
, если
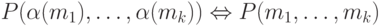
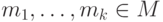 .
Аналогичным образом
.
Аналогичным образом  -местная функция
-местная функция  называется устойчивой
относительно
называется устойчивой
относительно  , если
, если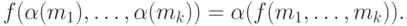
Теорема 27. Предикат, выразимый в данной интерпретации, устойчив относительно ее автоморфизмов.
Проведем доказательство этого (достаточно очевидного) утверждения формально.
Пусть  — некоторая оценка, то есть отображение, ставящее в
соответствие всем индивидным переменным некоторые элементы
носителя. Через
— некоторая оценка, то есть отображение, ставящее в
соответствие всем индивидным переменным некоторые элементы
носителя. Через  обозначим оценку, которая
получится, если к значению каждой переменной применить
отображение
обозначим оценку, которая
получится, если к значению каждой переменной применить
отображение  ; другими словами,
; другими словами, 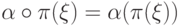 для любой переменной
для любой переменной  .
.
Первый шаг состоит в том, чтобы индукцией по построению терма  доказать такое утверждение: значение терма
доказать такое утверждение: значение терма  при
оценке
при
оценке  получается применением
получается применением  к
значению терма
к
значению терма  при оценке
при оценке  :
:
=\alpha([t](\pi)).](/sites/default/files/tex_cache/56a1c4f939275f70ce369119b5934175.png)
 .
.Теперь индукцией по построению формулы  легко доказать
такое утверждение:
легко доказать
такое утверждение:
 = [\varphi] (\pi).](/sites/default/files/tex_cache/36c01d1c8a468ca3c55aea6b20866c7d.png)
 используется, когда мы разбираем
случай кванторов. (В самом деле, если с одной стороны изоморфизма
берется какой-то объект, то взаимная однозначность позволяет
взять соответствующий ему объект с другой стороны изоморфизма.)
используется, когда мы разбираем
случай кванторов. (В самом деле, если с одной стороны изоморфизма
берется какой-то объект, то взаимная однозначность позволяет
взять соответствующий ему объект с другой стороны изоморфизма.)Теорема 27 позволяет доказать невыразимость какого-то предиката, предъявив автоморфизм интерпретации, относительно которого интересующий нас предикат неустойчив. Вот несколько примеров:
-
 Сигнатура содержит равенство
и отношение порядка. Интерпретация:
целые числа. Невыразимый предикат:
Сигнатура содержит равенство
и отношение порядка. Интерпретация:
целые числа. Невыразимый предикат: 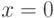 . Автоморфизм:
. Автоморфизм: 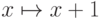 .
. -
 Сигнатура содержит равенство, отношение порядка и операцию
сложения. Интерпретация: рациональные числа. Невыразимый
предикат:
Сигнатура содержит равенство, отношение порядка и операцию
сложения. Интерпретация: рациональные числа. Невыразимый
предикат: 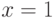 . Автоморфизм:
. Автоморфизм: 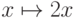 .
.Заметим, что сложение позволяет выразить предикат
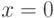 .
Кроме того, отметим, что вместо рациональных чисел можно взять
действительные (но не целые, так как в этом случае единица
описывается как наименьшее число, большее нуля).
.
Кроме того, отметим, что вместо рациональных чисел можно взять
действительные (но не целые, так как в этом случае единица
описывается как наименьшее число, большее нуля). -
 Сигнатура содержит равенство, порядок и константы
Сигнатура содержит равенство, порядок и константы  и
и  . Интерпретация: действительные числа. Невыразимый предикат:
. Интерпретация: действительные числа. Невыразимый предикат: 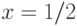 . (Автоморфизм упорядоченного множества
. (Автоморфизм упорядоченного множества  ,
сохраняющий
,
сохраняющий  и
и  , но не
, но не 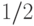 , построить легко.)
, построить легко.) -
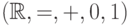 Сигнатура содержит равенство, сложение, константы
Сигнатура содержит равенство, сложение, константы  и
и  . Интерпретация: действительные числа. Одноместный предикат
. Интерпретация: действительные числа. Одноместный предикат  выразим для рациональных
выразим для рациональных  и невыразим
для иррациональных
и невыразим
для иррациональных  .
.В самом деле, выразимость для рациональных
 очевидна.
Невыразимость для иррациональных
очевидна.
Невыразимость для иррациональных  следует из того, что
для любых двух иррациональных
следует из того, что
для любых двух иррациональных 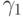 и
и 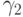 существует автоморфизм, переводящий
существует автоморфизм, переводящий 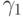 в
в 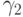 . (В
самом деле, рассмотрим
. (В
самом деле, рассмотрим  как бесконечномерное векторное пространство
над
как бесконечномерное векторное пространство
над  . Векторы
. Векторы 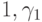 линейно независимы и
потому их можно дополнить до базиса Гамеля (подробности смотри в книжке по
теории множеств [6]). Сделаем то же самое с
векторами
линейно независимы и
потому их можно дополнить до базиса Гамеля (подробности смотри в книжке по
теории множеств [6]). Сделаем то же самое с
векторами 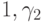 . Получатся равномощные базисы, после чего
мы берем
. Получатся равномощные базисы, после чего
мы берем  -линейный оператор, переводящий
-линейный оператор, переводящий  в
в  и
и 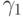 в
в 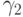 .)
.) -
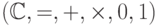 В сигнатуру входят предикат равенства, операции сложения и
умножения, а также константы
В сигнатуру входят предикат равенства, операции сложения и
умножения, а также константы  и
и  . Интерпретация:
комплексные числа. Предикат
. Интерпретация:
комплексные числа. Предикат  , где
, где  —
некоторое комплексное число, выразим для рациональных
—
некоторое комплексное число, выразим для рациональных  и невыразим
для иррациональных
и невыразим
для иррациональных  .
.В самом деле, если
 иррационально, то оно может быть
алгебраическим или трансцендентным. В первом случае рассмотрим
многочлен из
иррационально, то оно может быть
алгебраическим или трансцендентным. В первом случае рассмотрим
многочлен из ![\mathbb{Q}[x]](/sites/default/files/tex_cache/59c97504827af854ac13187c78ef7320.png) минимальной степени, обращающийся
в
минимальной степени, обращающийся
в  в точке
в точке  ; по предположению он имеет степень
больше
; по предположению он имеет степень
больше  и потому имеет другой корень
и потому имеет другой корень 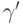 . В алгебре доказывается (с
использованием трансфинитной индукции или леммы Цорна, а также
базисов трансцендентности), что существует автоморфизм
. В алгебре доказывается (с
использованием трансфинитной индукции или леммы Цорна, а также
базисов трансцендентности), что существует автоморфизм 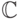 над
над  , переводящий
, переводящий  в
в 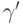 .
.В случае трансцендентного
 мы используем такой
факт: для любых трансцендентных
мы используем такой
факт: для любых трансцендентных 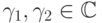 существует автоморфизм поля
существует автоморфизм поля 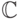 над
над  , который
переводит
, который
переводит 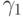 в
в 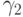 .
.Отметим, что для поля
 вместо
вместо 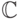 такое
рассуждение не проходит, так как это поле не имеет нетривиальных автоморфизмов.
(Отношение порядка выразимо: положительные числа суть квадраты,
поэтому любой автоморфизм сохраняет порядок. Поскольку
автоморфизм оставляет на месте все рациональные числа, он должен
быть тождественным.)
такое
рассуждение не проходит, так как это поле не имеет нетривиальных автоморфизмов.
(Отношение порядка выразимо: положительные числа суть квадраты,
поэтому любой автоморфизм сохраняет порядок. Поскольку
автоморфизм оставляет на месте все рациональные числа, он должен
быть тождественным.)В этом случае предикат
 выразим тогда и только тогда,
когда
выразим тогда и только тогда,
когда  — алгебраическое число. Это легко следует из
теоремы Тарского-Зайденберга.
— алгебраическое число. Это легко следует из
теоремы Тарского-Зайденберга.
61. Покажите, что предикат 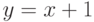 невыразим в интерпретации
невыразим в интерпретации 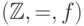 , где
, где  — одноместная функция
— одноместная функция 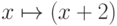 .
.
62. Покажите, что предикат 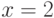 невыразим в множестве целых
положительных чисел с предикатами равенства и "
невыразим в множестве целых
положительных чисел с предикатами равенства и "  делит
делит  ".
".
