Языки первого порядка
Выразимые предикаты
Пусть фиксирована некоторая сигнатура  и ее
интерпретация с носителем
и ее
интерпретация с носителем  . Мы хотим определить понятие
выразимого (с помощью формулы данной сигнатуры в данной
интерпретации)
. Мы хотим определить понятие
выразимого (с помощью формулы данной сигнатуры в данной
интерпретации)  -местного предиката.
-местного предиката.
Выберем  переменных
переменных 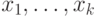 . Рассмотрим
произвольную формулу
. Рассмотрим
произвольную формулу  , все параметры которой содержатся в списке
, все параметры которой содержатся в списке 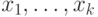 . Истинность этой формулы зависит только от
значений переменных
. Истинность этой формулы зависит только от
значений переменных 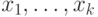 . Тем самым возникает
отображение
. Тем самым возникает
отображение 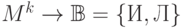 , то есть некоторый
, то есть некоторый  - местный предикат на
- местный предикат на  . Говорят, что этот предикат
выражается формулой
. Говорят, что этот предикат
выражается формулой  . Все предикаты, которые
можно получить таким способом, называются выразимыми.
(Ясно, что конкретный выбор списка переменных роли не играет.)
Соответствующие им подмножества множества
. Все предикаты, которые
можно получить таким способом, называются выразимыми.
(Ясно, что конкретный выбор списка переменных роли не играет.)
Соответствующие им подмножества множества 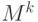 (области
истинности выразимых предикатов) также называют выразимыми.
(области
истинности выразимых предикатов) также называют выразимыми.
48. Докажите, что пересечение, объединение и разность двух выразимых
множеств являются выразимыми. Докажите, что проекция  -
мерного выразимого множества вдоль одной из "осей
координат" является
-
мерного выразимого множества вдоль одной из "осей
координат" является  -мерным выразимым множеством.
-мерным выразимым множеством.
Пример. Сигнатура содержит одноместный
функциональный символ  и двуместный предикатный символ
равенства (
и двуместный предикатный символ
равенства (  ). Рассмотрим интерпретацию этой сигнатуры. В
качестве носителя выберем натуральный ряд
). Рассмотрим интерпретацию этой сигнатуры. В
качестве носителя выберем натуральный ряд 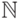 .
Символ
.
Символ  будет обозначать функцию прибавления единицы (можно считать
будет обозначать функцию прибавления единицы (можно считать  сокращением от слова successor — последователь). Знак равенства
интерпретируется как совпадение элементов.
сокращением от слова successor — последователь). Знак равенства
интерпретируется как совпадение элементов.
Легко проверить, что одноместный предикат "быть нулем" выразим в этой интерпретации, несмотря на то, что константы для нуля в сигнатуре не предусмотрено. В самом деле, он выражается формулой
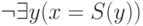
 .
.Еще проще выразить в этой сигнатуре двуместный предикат "быть
больше на  ", при этом даже не нужны кванторы:
", при этом даже не нужны кванторы:  .
.
Любопытно, что уже в такой простой ситуации можно сформулировать
содержательную задачу: выразить предикат 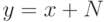 , где
, где  — большое число (скажем, миллиард), с помощью существенно более
короткой формулы, чем
— большое число (скажем, миллиард), с помощью существенно более
короткой формулы, чем 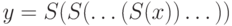 . Как ни
удивительно, это вполне возможно, и соответствующую формулу
вполне можно уместить на листе бумаги.
. Как ни
удивительно, это вполне возможно, и соответствующую формулу
вполне можно уместить на листе бумаги.
49. Докажите, что предикат 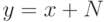 можно выразить формулой указанной
сигнатуры, длина которой есть
можно выразить формулой указанной
сигнатуры, длина которой есть  . (Указание. Если мы
научились выражать
. (Указание. Если мы
научились выражать  , можно выразить
, можно выразить 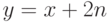 с
помощью формулы
с
помощью формулы
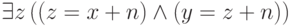
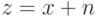 и
и 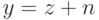 обозначены
соответствующие формулы). Это само по себе ничего не дает, так как длина
формулы увеличилась вдвое, но можно использовать такой трюк:
обозначены
соответствующие формулы). Это само по себе ничего не дает, так как длина
формулы увеличилась вдвое, но можно использовать такой трюк:
 в двоичной системе
счисления.)
в двоичной системе
счисления.)Можно доказать, что в этой сигнатуре кванторы почти не увеличивают
набор выразимых предикатов: всякий выразимый предикат будет выражаться
бескванторной формулой (возможно, гораздо более длинной),
если добавить к сигнатуре константу  .
Мы вернемся к этому вопросу в разделе "Элиминация кванторов".
.
Мы вернемся к этому вопросу в разделе "Элиминация кванторов".
Чтобы привыкнуть к понятию выразимости, рассмотрим еще один
пример. Пусть сигнатура содержит предикат равенства и
трехместный предикат  . Рассмотрим интерпретацию, в которой
носителем является множество точек плоскости, равенство
интерпретируется как совпадение точек, а
. Рассмотрим интерпретацию, в которой
носителем является множество точек плоскости, равенство
интерпретируется как совпадение точек, а 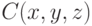 означает,
что точки
означает,
что точки  и
и  равноудалены от точки
равноудалены от точки  . Оказывается, что этого предиката достаточно, чтобы выразить более или менее
все традиционные понятия элементарной геометрии.
. Оказывается, что этого предиката достаточно, чтобы выразить более или менее
все традиционные понятия элементарной геометрии.
Как, например, записать, что три различные точки 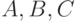 лежат
на одной прямой? Вот как: "не существует другой точки
лежат
на одной прямой? Вот как: "не существует другой точки 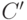 ,
которая находилась бы на тех же расстояниях от
,
которая находилась бы на тех же расстояниях от  и
и  , что и точка
, что и точка  ".
".
50. Напишите соответствующую формулу указанной сигнатуры.
Теперь легко выразить такое свойство четырех точек 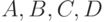 :
"точки
:
"точки  и
и  различны, точки
различны, точки  и
и  различны и прямые
различны и прямые 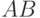 и
и 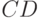 параллельны". В самом деле, надо
написать, что нет точки, которая бы одновременно лежала на одной прямой
с
параллельны". В самом деле, надо
написать, что нет точки, которая бы одновременно лежала на одной прямой
с  и
и  , а также на одной прямой с
, а также на одной прямой с  и
и  .
.
После этого можно выразить свойство четырех точек "быть вершинами
параллелограмма". Это позволяет переносить отрезок
параллельно себе. После этого несложно выразить такое свойство:
"расстояние 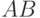 равно расстоянию
равно расстоянию 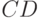 ".
".
51. Запишите соответствующую формулу.
Аналогичным образом можно двигаться и дальше.
52. Выразите свойство  трех точек
трех точек  ,
,  ,
,  .
(Указание. Напишите, что все прямые, проходящие через
.
(Указание. Напишите, что все прямые, проходящие через  ,
пересекаются с окружностью радиуса
,
пересекаются с окружностью радиуса  с центром в
с центром в  .)
.)
53. Запишите в виде формулы: (а) равенство треугольников; (б) равенство углов; (в) свойство угла быть прямым.
54. Рассмотрим естественную интерпретацию сигнатуры 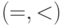 на
множестве целых чисел. Как выразить предикат
на
множестве целых чисел. Как выразить предикат 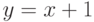 ?
?
55. Рассмотрим множество действительных чисел как интерпретацию
сигнатуры 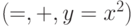 . Как выразить трехместный
предикат
. Как выразить трехместный
предикат 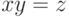 ?
?
56. Рассмотрим множество целых положительных чисел как интерпретацию
сигнатуры, содержащей равенство и двуместный предикат "  делит
делит  ". Выразите свойства "равняться единице" и "быть простым числом".
". Выразите свойства "равняться единице" и "быть простым числом".
57. Рассмотрим плоскость как интерпретацию сигнатуры, содержащей
предикат равенства (совпадение точек) и двуместный предикат "находиться
на расстоянии  ". Выразите двуместные предикаты
"находиться на расстоянии
". Выразите двуместные предикаты
"находиться на расстоянии  " и "находиться на
расстоянии не более
" и "находиться на
расстоянии не более  ". Выразите двуместный предикат
"находиться на расстоянии
". Выразите двуместный предикат
"находиться на расстоянии 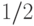 .
.
