Численные методы решения уравнений в частных производных
[+]
Опубликован: 25.10.2007 | Доступ: свободный | Студентов: 1279 / 290 | Оценка: 4.40 / 4.36 | Длительность: 21:57:00
Темы: Алгоритмы и дискретные структуры, Математика
Специальности: Математик
Теги: beta, алгоритмы, вторая производная, вычисления, диффузия, задача Коши, законы, искусственная жизнь, исследования, моделирование, невязка, обыкновенное дифференциальное уравнение, однородное уравнение, параллельные вычисления, потоки, собственный вектор, уравнения газовой динамики, уравнениями в частных производных, численное решение уравнений, элементы
Лекция 9:

Применение вариационных принципов для построения разностных схем
A
|
версия для печати
< Лекция 8 || Лекция 9: 123456 || Дополнительный материал  >

Проинтегрируем уравнение

$ \frac{{\partial}u}{{\partial}t} + {div}{\mathbf{W}} = 0 $

по элементарной ячейке разностной сетки. Имеем:

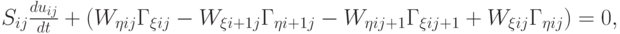$ {S_{ij} \frac{{du_{ij}}}{dt} + (W_{\eta ij} \Gamma_{\xi ij} - W_{\xi i + 1j} \Gamma_{\eta i + 1j} - W_{\eta ij + 1} \Gamma_{\xi ij + 1} + W_{\xi ij} \Gamma_{\eta ij} ) = 0, } $ ( 9.4)

где \Gamma — длины соответствующих ребер, Sij — площадь элементарной ячейки.

Так как координаты всех вершин выпуклого четырехугольника известны, то поиск длин, площадей и углов — элементарная геометрическая задача.

Уравнение (9.4}) — дискретный аналог уравнения (9.2). Если возможно определить все потоки в моменты времени tn, tn + 1, а после применить аппроксимацию (9.2) по времени с какими - либо весами, то будет построена разностная схема для расчета температуры.

Учтем, что

$ 2u \frac{{\partial}u}{{\partial}t} = - 2u{div}{\mathbf{W}}. $

Построим дискретный аналог (9.3):

\begin{gather*} F_{h} ({\mathbf{W}}^{h} ) = \sum\limits_{i, j \in \omega_{h}} \left[{S_{ij} \cdot \left(\sum\limits_{p, l = 0}^1{\frac{{W_{i + p, j + l}^2}}{{k_{ij}}}}\right) +}\right. \\ {\left. \begin{array}{l} {} \\ {} \\ {} \\ \end{array}2u_{ij}^{({\sigma})} (W_{\eta ij} \Gamma_{\xi ij} - W_{\xi i + 1j} \Gamma_{\eta i + 1j} - W_{\eta ij + 1} \Gamma_{\xi ij + 1} + W_{\xi ij} \Gamma_{\eta ij}) \right].}\end{gather*} ( 9.5)

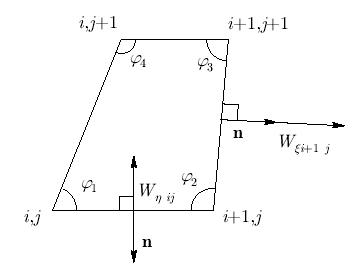
Скалярные квадраты, входящие в первое слагаемое дискретного аналога функционала, выражаются через контравариантные проекции следующим образом (рис. 9.7):

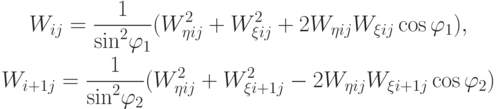
\begin{gather*} W_{ij} = \frac{1}{{{\sin}^2 \varphi_1}}(W_{\eta ij}^2 + W_{\xi ij}^2 + 2W_{\eta ij} W_{\xi ij} \cos \varphi_1 ), \\ W_{i + 1j} = \frac{1}{{{\sin}^2 \varphi_2}}(W_{\eta ij}^2 + W_{\xi i + 1j}^2 - 2W_{\eta ij} W_{\xi i + 1j} \cos \varphi_2 ) \end{gather*}

и т.д.


Рис. 9.7.

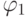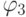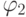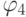Знак " + " или " - " определяется по правилу: компоненту потока приписывается знак " + ", если проекция потока сонаправлена с внешней нормалью, а знак " - " — если противонаправлена. Таким образом, для углов ячейки \varphi_1 и \varphi_3 получим знак " + " в последнем слагаемом (проекции одинаковых знаков), а для углов \varphi_2 и \varphi_4 — знак " - " (проекции теплового потока в произведении разных знаков).

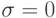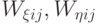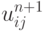Для получения явной схемы положим в (9.5) вес верхнего слоя по времени \sigma = 0 и дифференцируем (9.5) по всем W_{\xi ij}, W_{\eta ij}. Приравнивая производные нулю, получим схему для определения потоков, затем из (9.4) ищем все u_{ij}^{{n} + 1} .

Для построения неявной схемы в (9.4) считаем 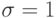\sigma = 1, а вместо (9.5) пишем следующую дискретизацию:

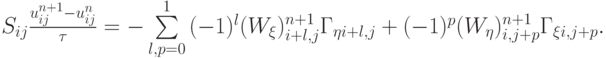
$ S_{ij} \frac{{u_{ij}^{{n} + 1} - u_{ij}^{n}}}{\tau} = - \sum\limits_{l, p = 0}^1 {(- 1)^{l}(W_\xi )_{i + l, j}^{{n} + 1} \Gamma_{\eta i + l, j} + (- 1)^{p} (W_\eta )_{i, j + p}^{{n} + 1} \Gamma_{\xi i, j + p} .} $

Выражая отсюда неизвестное пока значение 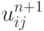u_{ij}^{{n} + 1} в (9.5), получим выражение, зависящее от 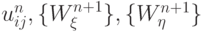u_{ij}^{n}, \{W_\xi ^{{n} + 1} \}, \{W_\eta ^{{n} + 1} \}, причем 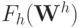F_{h} ({\mathbf{W}}^{h} ) есть сумма квадратов контравариантных проекций.

Дифференцируя, получим линейную систему уравнений для определения потоков. Можно показать, что матрица системы будет обладать следующими свойствами:

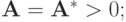
  1. {\mathbf{A}} = {\mathbf{A}}^* > 0;
  2. \mathbf{A} имеет ленточную структуру;
  3. \mathbf{A} является разреженной.

Можно применить эффективные итерационные методы решения системы.

Доказано, что неявная схема будет безусловно устойчивой, а явная — условно устойчивой.

Метод легко обобщается на случай k = k(x, y, u), если уравнение не вырождается. Кроме того, метод может быть обобщен и на случай других граничных условий (не обязательно отсутствия потоков). В этом случае в функционал (9.3) добавляются соответствующие интегралы по границам, а в (9.5) — суммы по поверхностям.

Подробнее об этих схемах можно прочитать в [19.2].

Дальше >>
< Лекция 8 || Лекция 9: 123456 || Дополнительный материал  >

Вопросы и ответы

вопросов: 0