Применение вариационных принципов для построения разностных схем
9.3. Вариационная схема для уравнения теплопроводности на криволинейной сетке
Рассмотрим линейное уравнение теплопроводности
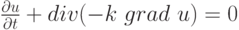 |
( 9.1) |
с условиями
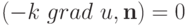
в ограниченной области  с криволинейной границей. При этом
нигде в
с криволинейной границей. При этом
нигде в  уравнение не вырождено, т.е. k(x, y) > 0 во всех точках области, включая граничные.
уравнение не вырождено, т.е. k(x, y) > 0 во всех точках области, включая граничные.
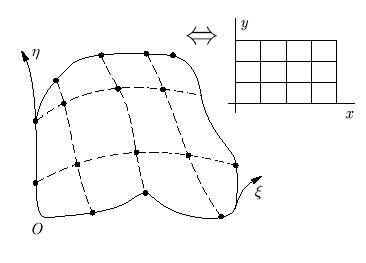
В области  каким - либо образом введена сетка с четырехугольными ячейками. Сетка считается связной, т.е. для любых двух вершин ячеек
существует ломаная, их соединяющая и состоящая из ребер ячеек (рис. 9.5).
каким - либо образом введена сетка с четырехугольными ячейками. Сетка считается связной, т.е. для любых двух вершин ячеек
существует ломаная, их соединяющая и состоящая из ребер ячеек (рис. 9.5).
Пусть сетка построена так, что существует преобразование, переводящее область  в параллелограмм (прямоугольник) с равномерной сеткой внутри. Тогда координатные линии x, y переходят в координатные кривые криволинейного базиса
в параллелограмм (прямоугольник) с равномерной сеткой внутри. Тогда координатные линии x, y переходят в координатные кривые криволинейного базиса 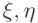 .
.
Перепишем уравнение (9.1) в виде системы
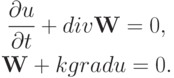 |
( 9.2) |
Рассмотрим функционал
![$ {F[u] = \int\limits_\Omega {\left({\frac{{({\mathbf{W}}, {\mathbf{W}})}}{k} - \frac{{\partial}}{{\partial}t}u^2}\right)dxdy}.} $](/sites/default/files/tex_cache/33a9ebe8f965cf08f08419bb98039200.png) |
( 9.3) |
Найдем ![\delta F[u]](/sites/default/files/tex_cache/da05f4aa9b98bbd6a60796ee4f0d8acd.png) :
:
![\begin{gather*}
\delta F[u] = \int\limits_\Omega {\delta \left({\frac{{({\mathbf{W}}, {\mathbf{W}})}}{k} -
\frac{{\partial}}{{\partial}t}u^2}\right)dxdy} = \\
= \int\limits_\Omega {\left({- 2{div}{\mathbf{W}} \cdot \delta u - 2 \delta u
\frac{{\partial}u}{{\partial}t} - 2u \frac{{\partial}}{{\partial t}} \delta u}\right)dxdy}, \\
\delta \frac{{({\mathbf{W}}, {\mathbf{W}})}}{k} = 2 \left({\frac{{\mathbf{W}}}{k}, \delta
{\mathbf{W}}}\right) = 2 \left({\frac{{\mathbf{W}}}{k}, - k {grad} \delta u}\right) =
- 2(\delta u, {div}{\mathbf{W}}).
\end{gather*}](/sites/default/files/tex_cache/9ef9049420fc08022187d4c044419678.png)
Отсюда при

Для построения разностной схемы введем дискретный аналог функционала 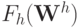 , т.е. в дискретном аналоге основной расчетной величиной будет поток тепла.
, т.е. в дискретном аналоге основной расчетной величиной будет поток тепла.
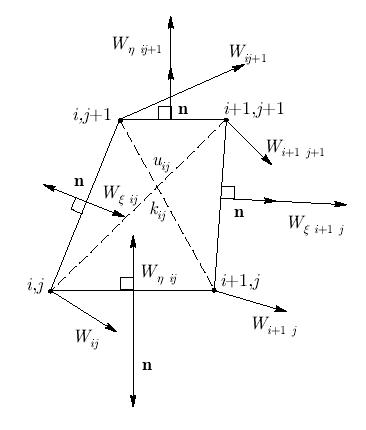
Прежде чем построить функционал, рассмотрим ячейку разностной сетки
(рис. 9.6). Температуру uij и коэффициент теплопроводности (или температуропроводности) kij отнесем к центру ячейки (точке пересечения диагоналей). В дальнейшем считаем, что термодинамические величины постоянны во всей ячейке. Векторы теплового потока отнесем к углам ячейки (рис. 9.6), а к центрам соответствующих ребер — проекции потоков на координатные оси. Считаем, что i увеличивается по мере увеличения координаты  ; j — по мере увеличения
; j — по мере увеличения 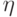 ; проекции векторов потока направлены вдоль соответствующих координатных линий. Заметим, что проекции потоков для двух ячеек сонаправлены с векторами внешней нормали, а для двух — противонаправлены.
; проекции векторов потока направлены вдоль соответствующих координатных линий. Заметим, что проекции потоков для двух ячеек сонаправлены с векторами внешней нормали, а для двух — противонаправлены.