НОУ ИНТУИТ | Теория и реализация языков программирования. Лекция 3: Языки и их представление

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 06.08.2007 | Доступ: свободный | Студентов: 1904 / 1056 | Оценка: 4.45 / 4.29 | Длительность: 18:50:00

Тема: Программирование

Специальности: Программист

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Предположим, что мы имеем алгоритм (то есть машину Тьюринга, которая всегда останавливается) для определения, остановится ли машина Тьюринга в данной конфигурации. Тогда следующим образом можно построить машину Тьюринга T, допускающую 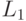L_1 .

Если дано слово x, T перечисляет слова x₁, x₂... пока не будет x_i = x.
T генерирует кодировку машины Тьюринга T_i.
Управление передается гипотетической машине, которая определяет останавливается ли T_i на входе x_i.
Если выясняется, что T_i не останавливается на входе x_i, то T останавливается и допускает x_i.
Если выясняется, что T_i останавливается на входе x_i, то управление передается универсальной машине Тьюринга, которая моделирует T_i на входе x_i. Поскольку T_i в конце концов останавливается, универсальная машина Тьюринга в конце концов останавливается и определяет допускает ли T_i слово x_i.

В любом случае T останавливается, допуская x_i в том случае, когда T_i отвергает x_i, и отвергая x_i, когда T_i допускает x_i.

Таким образом, из нашего предположения, что существует машина Тьюринга, которая определяет, останавливается ли произвольная машина Тьюринга, следует, что L₁ допускается некоторой машиной Тьюринга, а это противоречит доказанному выше. Это, в свою очередь, дает теорему:

Теорема 2.2. Не существует алгоритма для определения того, остановится ли произвольная машина Тьюринга в произвольной конфигурации.

Класс рекурсивных множеств

Теперь можно показать, что класс рекурсивных множеств является собственным подклассом класса рекурсивно перечислимых множеств. То есть существует множество, слова которого могут быть распознаны машиной Тьюринга, которая не останавливается на некоторых словах, не принадлежащих множеству, но не может быть распознано никакой машиной Тьюринга, которая останавливается на всех словах. Примером такого множества является дополнение к L₁.

Лемма 2.1. Если множество рекурсивно, то и его дополнение рекурсивно.

Доказательство. Если L - рекурсивное множество, 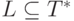$L \subseteq T^*$ , то существует Tm допускающая L и гарантированно останавливающаяся. Можно считать, что после допуска Tm не делает больше шагов. Построим Tm₁ по Tm, добавив новое состояние q как единственное допускающее состояние Tm₁. Правила Tm₁ включают все правила Tm, так что Tm₁ симулирует Tm. Кроме того, для каждой пары, составленной из недопускающего состояния и ленточного символа Tm, для которых у Tm переход не определен, Tm₁ переходит в состояние q и затем останавливается.

Таким образом Tm₁ симулирует Tm вплоть до остановки. Если Tm останавливается в одном из допускающих состояний, Tm₁ останавливается без допуска. Если Tm останавливается в одном из недопускающих состояний, значит не допускает вход. Тогда Tm₁ делает еще один переход в состояние q и допускает. Ясно, что Tm₁ допускает T^*\L.

Лемма 2.2. Пусть 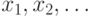$x_1, x_2, \ldots$ - нумерация всех слов некоторого конечного алфавита - и T₁, T₂, ...- нумерация всех машин Тьюринга с ленточными символами, выбранными из некоторого конечного алфавита, включающего -. Пусть $L_2 = \{x_i \mid x_i допускается T_i}$ . L₂ - рекурсивно перечислимое множество, дополнение которого не рекурсивно перечислимо.

Доказательство. Слова L₂ допускаются некоторой Tm, работающей следующим образом. Отметим, что Tm не обязательно останавливается на словах не из L₂.

Если дано x,Tm перечисляет предложения x₁, x₂,... пока не найдет x_i = x, определяя тем самым, что x - это i -е слово в перечислении.
Tm генерирует Tm_i и передает управление универсальной машине Тьюринга, которая симулирует Tm_i со входом x.
Если Tm_i останавливается со входом x_i и допускает, Tm останавливается и допускает; если Tm_i останавливается и отвергает x_i, то Tm останавливается и отвергает x_i. Наконец, если Tm_i не останавливается, то Tm не останавливается.
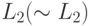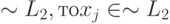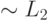Таким образом L₂ рекурсивно перечислимо, поскольку L₂ - это множество допускаемое Tm. Но дополнение к $L_2(\sim L_2)$ не может быть рекурсивно перечислимо, поскольку если T_j - машина Тьюринга, допускающая $\sim L_2, то x_j \in \sim L_2$ тогда и только тогда, когда x_j не допускается Tm_j. Это противоречит утверждению, что $\sim L_2$ - это язык, допускаемый T_j.

Теорема 2.3. Существует рекурсивно перечислимое множество, не являющееся рекурсивным.

Доказательство. Доказательство. По лемме 2.2 L₂ - рекурсивно перечислимое множество, дополнение которого не рекурсивно перечислимо. Если бы L₂ было рекурсивно, по лемме 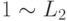$1 \sim L_2$ было бы рекурсивно, и следовательно рекурсивно перечислимо, что противоречит второй половине леммы 2.2.

Связь машин Тьюринга и грамматик типа 0

Докажем, что язык распознается машиной Тьюринга тогда и только тогда, когда он генерируется грамматикой типа 0. Для доказательства части "если" мы построим недетерминированную машину Тьюринга, которая будет недетерминированно выбирать выводы в грамматике и смотреть, является ли вывод входом. Если да, машина допускает вход.

Для доказательства части "только если" мы построим грамматику, которая недетерминированно генерирует представления терминальной строки и затем симулирует машину Тьюринга на этой строке. Если строка допускается некоторой Tm, строка конвертируется в терминальные символы, которые она представляет.

Теорема 2.4. Если L генерируется грамматикой типа 0, то L распознается машиной Тьюринга.

Доказательство. Пусть 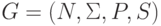$G = (N, \Sigma, P, S)$ - грамматика типа 0 и L = L(G). Опишем неформально недетерминированную машину Тьюринга Tm, допускающую L.

$Tm = (Q, \Sigma, \Gamma, D, q_0, F)$

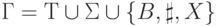
где $\Gamma=Т \cup \Sigma \cup \{B,\sharp,X\}$

Предполагается, что последние три символа не входят в $N \cup \Sigma$ .

Вначале Tm содержит на входной ленте 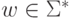$w \in \Sigma^*$ . Tm вставляет # перед w, сдвигая все символы w на одну ячейку вправо, и #S# после w, так что содержимым ленты становится #w#S#.

Теперь Tm недетерминированно симулирует вывод в G, начиная с S. Каждая сентенциальная форма вывода появляется по порядку между последними двумя #. Если некоторый выбор переходов ведет к терминальной строке, она сравнивается с w. Если они совпадают, Tm допускает.

Формально, пусть Tm имеет на ленте #w#A₁A₂...A_k#. Tm передвигает недетерминированно головку по A₁A₂...A_k, выбирая позицию i и константу r между 1 и максимальной длиной левой части любого правила вывода в P. Затем Tm проверяет подстроки A_iA_i+1...A_i+r-1. Если A_iA_i+1...A_i+r-1 - левая часть некоторого правила вывода из P, она может быть заменена на правую часть. Tm может сдвинуть A_i+rA_i+r+1...A_k# либо влево, либо вправо, освобождая или заполняя место, если правая часть имеет длину, отличную от r.

Из этой простой симуляции выводов в G видно, что Tm печатает на ленте строку вида 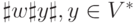$\sharp w \sharp y \sharp , y \in V^*$ в точности, если 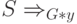$S \Rightarrow _{G*y}$ . Если y = w, Tm допускает L.

Теорема 2.5. Если L распознается некоторой машиной Тьюринга,то L генерируется грамматикой типа 0.

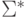Доказательство. Пусть $Tm = (Q, \Sigma, \Gamma, D, q_0, F)$ допускает L. Построим грамматику G, которая недерминированно генерирует две копии представления некоторого слова из $\Sigma^*$ и затем симулирует поведение Tm на одной из копий. Если Tm допускает слово, то G трансформирует вторую копию в терминальную строку. Если Tm не допускает L, то вывод никогда не приводит к терминальной строке.

Формально, пусть

$G=(N, \Sigma, P, A_1)$ , где $N=([\Sigma \cup \{e\}]\times \Gamma)\cup Q \cup \{A_1,A_2,A_3\}$

Продукции таковы:

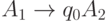
$A_1 \rightarrow q_0 A_2$
$A_2 \rightarrow [a, \; a] A_2$ для каждого $a \in \Sigma$
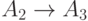
$A_2 \rightarrow A_3$
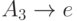
$A_3 \rightarrow [e,B]A_3$
$A_3 \rightarrow e$
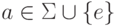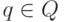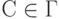$q[a, \; C] \rightarrow [a,E]p$ для каждого $a \in \Sigma \cup \{e\}$ и каждого $q \in Q$ и $С \in \Gamma$ такого, что $D(q, \; C)=(p,\; E, \; R)$
$[b, \; I]q[a, \; C] \rightarrow p[b, \; I][a, \; J]$ для каждого C, J, I из $\Gamma$ , a и b
$[a,C]q \rightarrow qaq, \; q[a, \; C] \rightarrow qaq, \; q \rightarrow e$ для каждого $a \in \Sigma \cup \{e\}, C \in \Gamma, q \in F$ .

Используя правила 1 и 2

$A_1\Rightarrow^* \; q_0[a_1, \; a_1][a_2, \; a_2]\ldots [a_n, \; a_n]A_2$

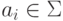где $a_i \in \Sigma$ для некоторого

Предположим, что Tm допускает строку a₁a₂ ... a_n. Тогда для некоторого m Tm использует не более, чем m ячеек справа от входа. Используя правило 3, затем правило 4 m раз, и наконец, правило 5, имеем

$A_1\Rightarrow^* \; q_0[a_1, \; a_1][a_2, \; a_2]\ldots [a_n, \; a_n][e, \; B]^m$

Начиная с этого момента могут быть использованы только правила 6 и 7, пока не сгенерируется допускающее состояние. Отметим, что первые компоненты ленточных символов в $(\Sigma \cup \{e\}) \times \Gamma$ никогда не меняются. Индукцией по числу шагов Tm можно показать, что если

$(q_0, \; a_1a_2 \ldots a_n, \;1)\vdash_{Tm*} \; (q, \; X_1 X_2 \ldots X_S, \; r)$ , то

$q_0[a_1,a_1][a_2,a_2] \ldots [a_n,a_n][e,B]^m \Rightarrow_{G*}$

$\Rightarrow_{G*} [a_1,X_1][a_2,X_2] \ldots [a_{r-1},X_{r-1}]q[a_r,X_r] \ldots [a_{n+m},X_{n+m}]$

где a₁, a₂, ... a_n принадлежат $\Sigma$ , a_n+1 = a_n+2 = ... a_n+m = e,

X₁ X₂, ...X_n+m принадлежат $\Gamma$ и X_S+1=X_S+2=...X_n+m=B

Предположение индукции тривиально для нуля шагов. Предположим, что оно справедливо для k - 1 шагов. Пусть

$\begin{multline} (q_0,a_1 a_2 \ldots a_n , \; 1)\vdash_{Tm*}\notag \\ \vdash_{Tm*} \; (q_1,X_1X_2 \ldots X_r,j_1)\vdash_{Tm*} \notag \\ \vdash_{Tm*}(q_2,Y_1Y_2 \ldots Y_S,j_2) \end{multline}$

за k шагов. По предположению индукции

$\begin{multline} q_0[a_1, a_1 ][a_2,a_2] \ldots [a_n,a_n][e,B]^m \Rightarrow_{G^*}\notag \\ \Rightarrow_{G^*}[a_1,X_1][a_2,X_2] \ldots [a_{r-1},X_{r-1}]q_1[a_{j1},X_{j1}]\ldots \notag \\ \ldots [a_{n+m},X_{n+m}] \end{multline}$

Пусть E = L, если j₂ = j₁ - 1 и E = R, если j₂ = j₁ + 1. В этом случае D(q₁, X_j1 ) = (q₂, Y_j1, E).

По правилам 6 или 7

$q_1[a_{j1},X_{j1}]\rightarrow [a_{j1},Y_{j1}]q_2 \; или$

$[ a_{j1-1},X_{j1-1} ] q_1[a_{j1},X_{j1}] \rightarrow q_2[a_{j1-1},X_{j1-1}][a_{j1},Y_{j1}]$

в зависимости от того, равно ли E значению R или L.

Теперь X_i = Y_i для всех $i \neq j_1$ .

Таким образом,

$\begin{multline} q_0[a_1,a_1][a_2,a_2] \ldots [a_n,a_n][e,B]^m \Rightarrow^{G*} \notag \\ \Rightarrow^{G*} \; [a_1,Y_1]q_2[a_{j2},Y_{j2}] \ldots [a_{n+m},Y_{n+m}] \end{multline}$

что доказывает предположение индукции.

По правилу 8, если $q \in F$ , легко показать, что

$[a_1,X_1] \ldots q[a_j,X_j] \ldots [a_{n+m},X_{n+m}]\Rightarrow^* a_1 a_2 \ldots a_n.$

Таким образом, G может генерировать a₁a₂ ... a_n, если a₁a₂ ... a_n допускается Tm. Таким образом, L(G) включает все слова, допускаемые Tm. Для завершения доказательства необходимо показать, что все слова из L(G) допускаются Tm. Индукцией доказывается, что 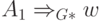$A_1 \Rightarrow_{G*} w$ только если w допускается Tm.

Дальше >>

Авторизоваться

Теория и реализация языков программирования

Языки и их представление

Класс рекурсивных множеств

Связь машин Тьюринга и грамматик типа 0

Вопросы и ответы