Применение теории нечетких множеств для обработки данных
Нечеткое подмножество  множества
множества  характеризуется функцией принадлежности
характеризуется функцией принадлежности ![\mu_A : X\rightarrow [0,1]](/sites/default/files/tex_cache/641ac5cb5091fb96886130affcd1dff5.png) , которая ставит в соответствие каждому элементу
, которая ставит в соответствие каждому элементу  число
число  из интервала [0,1], характеризующее степень принадлежности элемента
из интервала [0,1], характеризующее степень принадлежности элемента  подмножеству
подмножеству  . Причем 0 и 1 представляют собой соответственно низшую и высшую степень принадлежности элемента к определенному подмножеству.
. Причем 0 и 1 представляют собой соответственно низшую и высшую степень принадлежности элемента к определенному подмножеству.
Точкой перехода  называется элемент
называется элемент  множества
множества  , для которого
, для которого 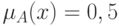 .
.
Если в классической теории множеств понятие характеристического функционала играет второстепенную роль, то для нечетких множеств функция принадлежности становится единственно возможным средством их описания. С формальной точки зрения нет необходимости различать нечеткое множество и его функцию принадлежности. В этом смысле теория нечетких множеств (ТНМ) можно рассматривать как теорию функций специального вида - обобщенных характеристических функций [10] .
Пусть  - универсальное множество,
- универсальное множество,  - элемент
- элемент  , а
, а  - определенное свойство. Обычное (четкое) подмножество
- определенное свойство. Обычное (четкое) подмножество  универсального множества
универсального множества  , элементы которого удовлетворяют свойство
, элементы которого удовлетворяют свойство  , определяется как множество упорядоченной пары
, определяется как множество упорядоченной пары  , где
, где  - характеристическая функция, принимающая значение 1, когда x удовлетворяет свойство
- характеристическая функция, принимающая значение 1, когда x удовлетворяет свойство  , и 0 - в другом случае.
, и 0 - в другом случае.
Нечеткое подмножество отличается от обычного тем, что для элементов  из
из  нет однозначного ответа "нет" относительно свойства
нет однозначного ответа "нет" относительно свойства  . В связи с этим, нечеткое подмножество
. В связи с этим, нечеткое подмножество  универсального множества
универсального множества  определяется как множество упорядоченной пары
определяется как множество упорядоченной пары 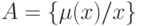 где
где  - характеристическая функция принадлежности (или просто функция принадлежности), принимающая значение в некотором упорядоченном множестве
- характеристическая функция принадлежности (или просто функция принадлежности), принимающая значение в некотором упорядоченном множестве  (например,
(например, ![M = [0,1]](/sites/default/files/tex_cache/8deb1b9ae86b7d90de59987cddd22680.png) ).
).
Функция принадлежности указывает степень (или уровень) принадлежности элемента  к подмножеству
к подмножеству  . Множество
. Множество  называют множеством принадлежностей. Если
называют множеством принадлежностей. Если 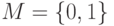 , тогда нечеткое подмножество
, тогда нечеткое подмножество  может рассматриваться как обычное или четкое множество.
может рассматриваться как обычное или четкое множество.
Пусть ![M = [0,1]](/sites/default/files/tex_cache/8deb1b9ae86b7d90de59987cddd22680.png) и
и  - нечеткое множество с элементами из универсального множества
- нечеткое множество с элементами из универсального множества  и множеством принадлежностей
и множеством принадлежностей 
Величина  называется высотою нечеткого множества
называется высотою нечеткого множества  . Нечеткое множество
. Нечеткое множество  является нормальным, если его высота равняется 1, то есть верхняя граница ее функции принадлежности равняется 1
является нормальным, если его высота равняется 1, то есть верхняя граница ее функции принадлежности равняется 1  . При
. При 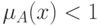 нечеткое множество называется субнормальным.
нечеткое множество называется субнормальным.
Нечеткое множество является пустым, если для каждого 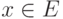
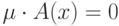 . Непустое субнормальное множество можно нормализировать по формуле
. Непустое субнормальное множество можно нормализировать по формуле
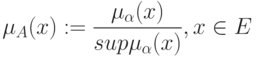 |
( 12.4) |
Нечеткое множество является унимодальным, если лишь для одного  из
из  .
.
Носителем нечеткого множества  является обычное подмножество со свойством
является обычное подмножество со свойством 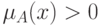 , то есть носитель
, то есть носитель 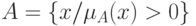 для каждого
для каждого 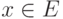 .
.
Элементы 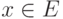 , для которых
, для которых 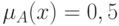 называются точками перехода множества
называются точками перехода множества 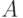 .
.
Как считают авторы [11,7,9] для нечетких множеств можно применить визуальное представление. Рассмотрим прямоугольную систему координат, на оси ординат которой откладываются значение  , на оси абсцисс в произвольном порядке расположены элементы
, на оси абсцисс в произвольном порядке расположены элементы 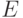 . Если
. Если 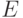 по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами [14].
по своей природе упорядочено, то этот порядок желательно сохранить в расположении элементов на оси абсцисс. Такое представление делает наглядными простые операции над нечеткими множествами [14].
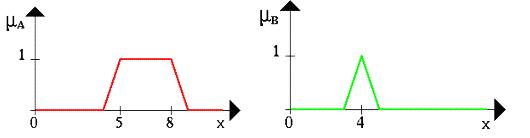
Пусть 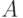 нечеткий интервал между 5 до 8 и
нечеткий интервал между 5 до 8 и 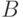 нечеткое число около 4 (см.Рисунок 12. 1).
нечеткое число около 4 (см.Рисунок 12. 1).
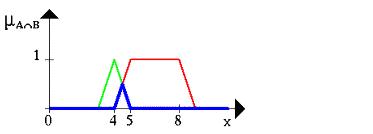
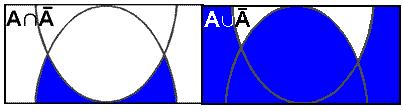
Проиллюстрируем нечеткое множество между 5 и 8 И (AND) около 4 (см. Рисунок 12. 2).
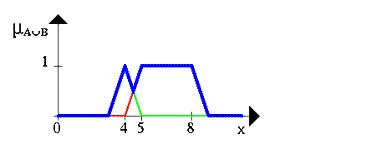
Нечеткое множество между 5 и 8 ИЛИ (OR) около 4 показано на следующем рисунке (см. Рисунок 12.3).
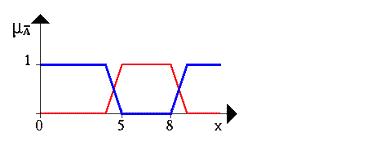
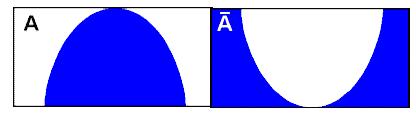
Следующий рисунок иллюстрирует операцию отрицания нечеткого множества A (см.Рисунок 12.4).
На следующем рисунке закрашенная часть соответствует нечеткому множеству A и изображает область значений А и всех нечетких множеств, содержащихся в A (см. Рисунок 12. 5).
Остальные рисунки изображают соответственно 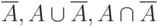 (см. рисунок 12.6.
(см. рисунок 12.6.