Оптимальное кодирование
12.4. Код Шеннона-Фано
Мы видели, как можно построить оптимальный код (имеющий
минимальную среднюю длину) для данного набора частот.
Однако эта конструкция не дает никакой оценки для средней
длины оптимального кода (как функции от частот 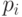 ).
Следующие задачи указывает такую оценку (с абсолютной
погрешностью не более
).
Следующие задачи указывает такую оценку (с абсолютной
погрешностью не более  ).
).
12.4.1.
Показать, что для любых положительных частот 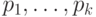 (в сумме равных единице) существует код
средней длиной не более
(в сумме равных единице) существует код
средней длиной не более 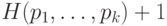 , где
функция
, где
функция  (называемая энтропией Шеннона )
определяется формулой
(называемая энтропией Шеннона )
определяется формулой

Решение. Если частоты 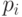 представляют собой целые (отрицательные) степени двойки, то это утверждение почти
очевидно. Положим
представляют собой целые (отрицательные) степени двойки, то это утверждение почти
очевидно. Положим 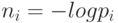 (здесь и далее все
логарифмы двоичные). Тогда
(здесь и далее все
логарифмы двоичные). Тогда 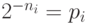 и потому для
чисел
и потому для
чисел 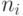 выполнено неравенство Крафта-Макмиллана. По
задаче 12.2.3. можно построить префиксный код
с длинами кодовых слов
выполнено неравенство Крафта-Макмиллана. По
задаче 12.2.3. можно построить префиксный код
с длинами кодовых слов 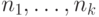 , и средняя длина
этого кода будет равна
, и средняя длина
этого кода будет равна 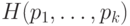 (и даже единицу
добавлять не надо).
(и даже единицу
добавлять не надо).
Эта единица пригодится, если  не целые. В этом
случае надо взять наименьшее
не целые. В этом
случае надо взять наименьшее 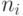 , при котором
, при котором 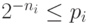 . Для таких
. Для таких 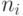 выполняется неравенство Крафта
Макмиллана, и они больше
выполняется неравенство Крафта
Макмиллана, и они больше  не более чем на
единицу (потому и после усреднения ухудшение будет не более
чем не единицу.
не более чем на
единицу (потому и после усреднения ухудшение будет не более
чем не единицу.
Построенный на основе этой задачи код называется кодом Шеннона-Фано.
Это построение легко извлекается из решения
задачи 12.2.3.: рассматривая числа  (наименьшие целые числа, для которых
(наименьшие целые числа, для которых 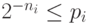 ) в порядке убывания, мы отводим для каждого из
них кодовое слово и соответствующий участок отрезка
) в порядке убывания, мы отводим для каждого из
них кодовое слово и соответствующий участок отрезка ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) слева направо.
слева направо.
При этом мы проигрываем в длине кода (по сравнению с оптимальным
кодом) не более единицы: как мы сейчас увидим, средняя длина
любого (в том числе и оптимального) кода не меньше 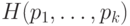 .
.
12.4.2.
(Для знакомых с математическим анализом) Доказать, что (при
данных положительных частотах, в сумме дающих единицу) средняя
длина любого (однозначного) кода не меньше 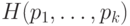 .
.
Решение. Имея в виду неравенство Крафта-Макмиллана, мы должны доказать такой факт: если
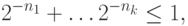
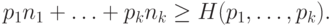
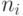 , не обязательно целых. Удобно
перейти от
, не обязательно целых. Удобно
перейти от 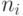 к величинам
к величинам 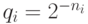 ; интересующее
нас утверждение тогда гласит, что если
; интересующее
нас утверждение тогда гласит, что если 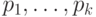 и
и  - два набора положительных чисел,
и сумма чисел в каждом равна единице, то
- два набора положительных чисел,
и сумма чисел в каждом равна единице, то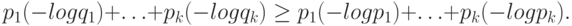
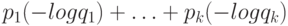
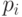 как функция на
множестве всех положительных
как функция на
множестве всех положительных  , в сумме
равных единице) достигает минимума при
, в сумме
равных единице) достигает минимума при  . Область
определения этой функции есть внутренность симплекса
(треугольника при
. Область
определения этой функции есть внутренность симплекса
(треугольника при 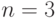 , тетраэдра при
, тетраэдра при 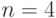 и т.д.) и при приближении к границе одно из
и т.д.) и при приближении к границе одно из  становится малым, а его
минус логарифм уходит в бесконечность. Значит, минимум
функции достигается внутри области. В точке минимума градиент
становится малым, а его
минус логарифм уходит в бесконечность. Значит, минимум
функции достигается внутри области. В точке минимума градиент 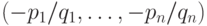 должен быть перпендикулярен
плоскости, на которой функция определена (иначе сдвиг вдоль
этой плоскости уменьшал бы функцию), то есть все
должен быть перпендикулярен
плоскости, на которой функция определена (иначе сдвиг вдоль
этой плоскости уменьшал бы функцию), то есть все 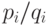 равны. Поскольку
равны. Поскольку 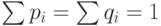 , то это означает,
что
, то это означает,
что  .
.Другое объяснение: функция  выпукла вверх, поэтому
для любых неотрицательных коэффициентов
выпукла вверх, поэтому
для любых неотрицательных коэффициентов 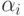 , в сумме
равных единице, и для любых точек
, в сумме
равных единице, и для любых точек  из области
определения логарифма выполняется неравенство
из области
определения логарифма выполняется неравенство
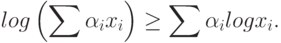
 ,
, 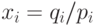 ; в левой
части
будет логарифм единицы, то есть нуль, а
; в левой
части
будет логарифм единицы, то есть нуль, а  есть как раз разность между левой и правой частями
доказываемого неравенства.
есть как раз разность между левой и правой частями
доказываемого неравенства.Велика ли экономия от использования кодов, описанных в этом
разделе? Это, конечно, зависит от частот букв: если они все
одинаковые, то никакой экономии не будет. Легко заметить,
что в русском языке разные буквы имеют разную частоту.
Если, скажем, в текстах (TeX-файлах) этого курса (на
момент эксперимента) оставить только  строчные русские
буквы от "а" до "я", а все остальные символы не
учитывать, то самой частой буквой будет буква "о"
(частота
строчные русские
буквы от "а" до "я", а все остальные символы не
учитывать, то самой частой буквой будет буква "о"
(частота  ), а самой редкой - твердый знак (частота
), а самой редкой - твердый знак (частота  ). Значение энтропии Шеннона при этом будет
равно
). Значение энтропии Шеннона при этом будет
равно 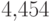 (сравните с
(сравните с 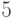 битами, необходимыми для кодирования
битами, необходимыми для кодирования 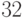 букв). Выигрыш не так велик. Он будет
больше, если учитывать также и другие символы (прописные
буквы, знаки препинания и др.), которые встречаются
в тексте гораздо реже или вовсе не встречаются.
Наконец, можно кодировать не буквы, а двухбуквенные
комбинации или еще что-нибудь. Именно так поступают
популярные программы сжатия информации (типа zip),
которые позволяют сократить многие тексты в полтора-два
раза (а некоторые другие файлы данных - и в большее число
раз).
букв). Выигрыш не так велик. Он будет
больше, если учитывать также и другие символы (прописные
буквы, знаки препинания и др.), которые встречаются
в тексте гораздо реже или вовсе не встречаются.
Наконец, можно кодировать не буквы, а двухбуквенные
комбинации или еще что-нибудь. Именно так поступают
популярные программы сжатия информации (типа zip),
которые позволяют сократить многие тексты в полтора-два
раза (а некоторые другие файлы данных - и в большее число
раз).
12.4.3.
Компания M. утверждает, что ее новая программа суперсжатия
файлов позволяет сжать любой файл длиной больше 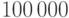 байтов по крайней мере на
байтов по крайней мере на  без потери
информации (можно восстановить исходный файл по его сжатому
варианту). Доказать, что она врет.
без потери
информации (можно восстановить исходный файл по его сжатому
варианту). Доказать, что она врет.
