Оптимальное кодирование
12.2. Неравенство Крафта-Макмиллана
Зачем вообще нужны коды с разной длиной кодовых слов? Дело в том, что на практике разные символы алфавита встречаются с разной частотой, и выгодно закодировать частые символы короткими словами. (Это соображение, кстати, учитывалось при составлении азбуки Морзе.)
Пусть для каждой буквы  алфавита
алфавита  фиксирована ее частота
фиксирована ее частота  - положительное число, причем суммы частот
всех букв равны единице. Тогда для любого кода
- положительное число, причем суммы частот
всех букв равны единице. Тогда для любого кода  можно
определить среднюю длину этого кода как сумму
можно
определить среднюю длину этого кода как сумму

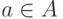 , где
, где 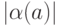 - длина
кодового
слова
- длина
кодового
слова  буквы
буквы  . (Смысл этого определения:
если
в слове длины
. (Смысл этого определения:
если
в слове длины  буква
буква  встречается с частотой
встречается с частотой  ,
то таких букв будет
,
то таких букв будет 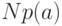 и на их кодирование уйдет
и на их кодирование уйдет  битов; общая длина кода будет
битов; общая длина кода будет  и в среднем на кодирование каждой буквы
уйдет
и в среднем на кодирование каждой буквы
уйдет  битов.)
битов.)Теперь возникает задача: для данных частот построить однозначный код минимальной средней длины. Теоретически это можно сделать перебором (если в коде есть хотя бы одно очень длинное кодовое слово, то его средняя длина велика, поэтому такие коды можно не рассматривать; остается конечное число вариантов). Но можно обойтись и без перебора, и в этом разделе мы научимся это делать.
Для начала поймем, что мешает нам выбирать кодовые слова
короткими. Оказывается, что есть ровно одно препятствие:
длины 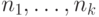 кодовых слов должны удовлетворять
неравенству
кодовых слов должны удовлетворять
неравенству

12.2.1. Проверить, что оно выполнено для рассмотренных выше примеров однозначных кодов.
12.2.2. Доказать, что для всякого префиксного кода выполняется неравенство Крафта-Макмиллана.
Решение. Отрезок ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) можно разбить на две половины.
Назовем левую
можно разбить на две половины.
Назовем левую  , а правую
, а правую 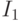 . Каждую из них
разобьем
пополам: отрезок
. Каждую из них
разобьем
пополам: отрезок  разделится на левую
половину
разделится на левую
половину  и правую
и правую  , аналогично
, аналогично 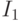 делится на
делится на  и
и 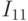 . И так
далее: любому
двоичному слову
. И так
далее: любому
двоичному слову  соответствует отрезок
соответствует отрезок  . Длина
этого отрезка есть
. Длина
этого отрезка есть  , где
, где 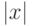 - длина
слова
- длина
слова  .
Если слово
.
Если слово  является началом слова
является началом слова  , то
отрезок
, то
отрезок  содержит отрезок
содержит отрезок 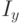 ; если ни одно из
слов
; если ни одно из
слов  и
и  не
является началом другого, то отрезки
не
является началом другого, то отрезки  и
и 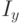 не
перекрываются (на том знаке, где
не
перекрываются (на том знаке, где  и
и  впервые
расходятся,
впервые
расходятся,  и
и 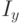 попадают в разные
половины).
попадают в разные
половины).
Рассмотрим теперь отрезки, соответствующие словам префиксного кода. Они не перекрываются. А значит, сумма их длин не больше единицы, что и дает неравенство Крафта-Макмиллана.
12.2.3.
Пусть даны  целых положительных чисел
целых положительных чисел 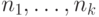 ,
удовлетворяющие неравенству Крафта-Макмиллана. Доказать,
что можно построить префиксный код для
,
удовлетворяющие неравенству Крафта-Макмиллана. Доказать,
что можно построить префиксный код для  -буквенного алфавита
с длинами кодовых слов
-буквенного алфавита
с длинами кодовых слов 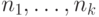 .
.
Решение. И здесь полезно использовать соответствие между словами
и отрезками и представлять себе дело так: у нас есть единичный
отрезок ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) , и мы выделяем его части пользователям по
требованию. Если пользователь приходит с числом
, и мы выделяем его части пользователям по
требованию. Если пользователь приходит с числом 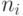 , то это
значит, что ему надо выдать в пользование один из отрезков
длиной
, то это
значит, что ему надо выдать в пользование один из отрезков
длиной  , соответствующих кодовым словам
длины
, соответствующих кодовым словам
длины 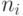 .
(Тем самым годятся не любые отрезки такой длины, а лишь "
правильно расположенные".) Код должен быть префиксным, это
значит, что отрезки разных пользователей не должны
перекрываться. Нам дано, что суммарная длина всех требований не
больше единицы. Как их удовлетворить? Можно отводить место слева
направо, при этом рассматривать требования в порядке убывания
длин (тогда более короткие отрезки будут правильно расположены
после предыдущих более длинных).
.
(Тем самым годятся не любые отрезки такой длины, а лишь "
правильно расположенные".) Код должен быть префиксным, это
значит, что отрезки разных пользователей не должны
перекрываться. Нам дано, что суммарная длина всех требований не
больше единицы. Как их удовлетворить? Можно отводить место слева
направо, при этом рассматривать требования в порядке убывания
длин (тогда более короткие отрезки будут правильно расположены
после предыдущих более длинных).
12.2.4.
Показать, что выделять кодовые слова (место на отрезке)
можно и в порядке поступления требований (как иногда
говорят, в "режиме on-line"): пользователь приходит
с числом 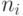 и уходит с правильно расположенным отрезком
длины
и уходит с правильно расположенным отрезком
длины  , причем если выполнено неравенство Крафта
Макмиллана, то никто не уйдет обиженным (всем хватит места,
и перераспределять его не придется).
, причем если выполнено неравенство Крафта
Макмиллана, то никто не уйдет обиженным (всем хватит места,
и перераспределять его не придется).
Указание. Нужно поддерживать свободное пространство как объединение правильно расположенных отрезков попарно различных длин, выделяя каждому пользователю кусок из кратчайшего подходящего отрезка и доразбивая остаток.
12.2.5. Показать, что неравенство Крафта-Макмиллана выполняется не только для любого префиксного кода, но и вообще для любого однозначного кода. (Именно это доказал Макмиллан; Крафт доказал неравенство для префиксных кодов.)
Решение. Есть разные способы решить эту задачу; мы приведем
простое и красивое, хотя и несколько загадочное, решение. Пусть
имеется однозначный код с  кодовыми словами
кодовыми словами  .
Нам надо доказать, что их длины
.
Нам надо доказать, что их длины  удовлетворяют
неравенству Крафта-Макмиллана. Представим себе, что вместо
нулей и единиц используются символы
удовлетворяют
неравенству Крафта-Макмиллана. Представим себе, что вместо
нулей и единиц используются символы  и
и  (какая
разница, из чего составлять коды?). Запишем формально сумму всех кодовых
слов как алгебраическое выражение
(какая
разница, из чего составлять коды?). Запишем формально сумму всех кодовых
слов как алгебраическое выражение

 и
и  , в котором одночлены записаны как
произведения переменных
, в котором одночлены записаны как
произведения переменных  и
и  , без возведения
в степень). Теперь (еще более странное на первый взгляд
действие) возведем это выражение в степень
, без возведения
в степень). Теперь (еще более странное на первый взгляд
действие) возведем это выражение в степень  (произвольное натуральное число) и раскроем скобки,
сохраняя порядок переменных (не собирая вместе одинаковые
переменные) в одночленах:
(произвольное натуральное число) и раскроем скобки,
сохраняя порядок переменных (не собирая вместе одинаковые
переменные) в одночленах:
 (которые теперь
записываются
как
(которые теперь
записываются
как  ) и для
) и для 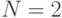 получаем
получаем
Теперь подставим  в наше равенство (если оно верно для букв, то оно верно и для любых их числовых значений). Слева
получится
в наше равенство (если оно верно для букв, то оно верно и для любых их числовых значений). Слева
получится

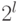 слагаемых
длины
слагаемых
длины  , каждое из которых равно
, каждое из которых равно 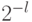 , и потому
слагаемые данной длины в сумме не превосходят единицы,
а правая часть не превосходит максимальной длины слагаемых,
то есть
, и потому
слагаемые данной длины в сумме не превосходят единицы,
а правая часть не превосходит максимальной длины слагаемых,
то есть  . Итак, получаем, что
. Итак, получаем, что
 . Если основание степени в левой
части больше единицы, то при больших
. Если основание степени в левой
части больше единицы, то при больших  это неравенство
нарушится (показательная функция растет быстрее линейной).
Поэтому для однозначного кода выполняется неравенство
Крафта-Макмиллана.
это неравенство
нарушится (показательная функция растет быстрее линейной).
Поэтому для однозначного кода выполняется неравенство
Крафта-Макмиллана.