Синтаксический разбор слева направо (LR)
Сейчас мы рассмотрим еще один метод синтаксического разбора, называемый LR(1)-разбором, а также некоторые упрощенные его варианты.
16.1. LR-процессы
Два отличия LR(1)-разбора от LL(1)-разбора: во-первых, строится не левый вывод, а правый, во-вторых, он строится не с начала, а с конца. (Вывод в КС-грамматике называется правым, если на каждом шаге замене подвергается самый правый нетерминал.)
16.1.1. Доказать, что если слово, состоящее из терминалов, выводимо, то оно имеет правый вывод.
Нам будет удобно смотреть на правый вывод "задом
наперед". Определим понятие LR-процесса над словом  . В этом процессе, помимо
. В этом процессе, помимо  , будет участвовать и другое слово
, будет участвовать и другое слово  , которое может содержать как терминалы, так и нетерминалы. Вначале слово
, которое может содержать как терминалы, так и нетерминалы. Вначале слово  пусто. В ходе LR-процесса разрешены два вида действий:
пусто. В ходе LR-процесса разрешены два вида действий:
- можно перенести первый символ слова
 (его называют очередным символом и обозначают Next ) в конец слова
(его называют очередным символом и обозначают Next ) в конец слова  , удалив его из
, удалив его из  (это действие называют сдвигом );
(это действие называют сдвигом ); - если правая часть одного из правил грамматики
оказалась концом слова
 , то разрешается заменить ее на нетерминал, стоящий в левой части этого правила; при этом слово
, то разрешается заменить ее на нетерминал, стоящий в левой части этого правила; при этом слово  не меняется. (Это действие называют сверткой, или приведением.
не меняется. (Это действие называют сверткой, или приведением.
Отметим, что LR-процесс не является детерминированным: в одной и той же ситуации могут быть разрешены разные действия.
Говорят, что LR-процесс на слове  успешно завершается, если слово
успешно завершается, если слово  становится пустым, а в слове
становится пустым, а в слове  остается единственный нетерминал - начальный нетерминал грамматики.
остается единственный нетерминал - начальный нетерминал грамматики.
16.1.2.
Доказать, что для любого слова  (из терминалов)
успешно завершающийся LR-процесс существует тогда и только
тогда, когда слово
(из терминалов)
успешно завершающийся LR-процесс существует тогда и только
тогда, когда слово  выводимо в грамматике. В ходе доказательства установить взаимно однозначное соответствие между правыми выводами и успешно завершающимися LR-процессами.
выводимо в грамматике. В ходе доказательства установить взаимно однозначное соответствие между правыми выводами и успешно завершающимися LR-процессами.
Решение. При сдвиге слово 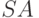 не меняется, при свертке слово
не меняется, при свертке слово 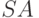 подвергается преобразованию, обратному шагу вывода. Этот вывод будет правым, так как сворачивается конец
подвергается преобразованию, обратному шагу вывода. Этот вывод будет правым, так как сворачивается конец  , а в
, а в  все символы - терминальные. Таким образом, каждому LR-процессу соответствует правый вывод. Обратное соответствие: пусть дан правый вывод. Представим себе, что за последним нетерминалом в слове стоит перегородка. Применив к этому нетерминалу правило грамматики, мы должны сдвинуть перегородку влево (если правая часть правила кончается на терминал). Разбивая этот сдвиг на отдельные шаги, получим процесс, в точности обратный LR-процессу.
все символы - терминальные. Таким образом, каждому LR-процессу соответствует правый вывод. Обратное соответствие: пусть дан правый вывод. Представим себе, что за последним нетерминалом в слове стоит перегородка. Применив к этому нетерминалу правило грамматики, мы должны сдвинуть перегородку влево (если правая часть правила кончается на терминал). Разбивая этот сдвиг на отдельные шаги, получим процесс, в точности обратный LR-процессу.
Поскольку в ходе LR-процесса все изменения в слове  происходят с правого конца, слово
происходят с правого конца, слово  называют стеком LR-процесса .
называют стеком LR-процесса .
Задача построения правого вывода для данного слова
сводится, таким образом, к правильному выбору очередного шага
LR-процесса. Нам нужно решить, будем ли мы делать сдвиг или
свертку, и если свертку, то по какому правилу - ведь
подходящих правил может быть несколько. В LR(1)-алгоритме это
решение принимается на основе  и первого символа слова
и первого символа слова  ; если используется только
; если используется только  , то говорят о LR(0)-алгоритме.
(Точные определения смотри ниже.)
, то говорят о LR(0)-алгоритме.
(Точные определения смотри ниже.)
Пусть фиксирована грамматика, в которой из любого нетерминала можно вывести какое-либо слово из терминалов. (Это ограничение мы будет всегда предполагать выполненным.)
Пусть  - одно из правил грамматики ( K - нетерминал, U - слово из терминалов и нетерминалов). Определим множество слов (из терминалов и нетерминалов), называемое левым контекстом правила
- одно из правил грамматики ( K - нетерминал, U - слово из терминалов и нетерминалов). Определим множество слов (из терминалов и нетерминалов), называемое левым контекстом правила  . (Обозначение:
. (Обозначение:  .) По определению
в него входят все слова, которые являются содержимым стека
непосредственно перед сверткой U в K в ходе
некоторого успешно завершающегося LR-процесса.
.) По определению
в него входят все слова, которые являются содержимым стека
непосредственно перед сверткой U в K в ходе
некоторого успешно завершающегося LR-процесса.
16.1.3. Переформулировать это определение на языке правых выводов.
Решение. Рассмотрим все правые выводы вида

 . Чтобы убедиться в этом, следует вспомнить, что мы предполагаем, что из любого нетерминала можно вывести какое-то слово из терминалов, так что правый вывод слова XUA может быть продолжен до правого вывода какого-то слова из терминалов.
. Чтобы убедиться в этом, следует вспомнить, что мы предполагаем, что из любого нетерминала можно вывести какое-то слово из терминалов, так что правый вывод слова XUA может быть продолжен до правого вывода какого-то слова из терминалов.16.1.4.
Все слова из  кончаются,
очевидно, на U. Доказать, что если у всех них этот
конец U отбросить, то полученное множество слов не
зависит от того, какое из правил для нетерминала K
выбрано. (Это множество обозначается
кончаются,
очевидно, на U. Доказать, что если у всех них этот
конец U отбросить, то полученное множество слов не
зависит от того, какое из правил для нетерминала K
выбрано. (Это множество обозначается 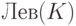 .)
.)
Решение. Из предыдущей задачи ясно, что 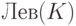 - это все, что может появиться в правых выводах левее самого правого нетерминала K.
- это все, что может появиться в правых выводах левее самого правого нетерминала K.
16.1.5.
Доказать, что в предыдущей фразе можно отбросить слова "
самого правого": 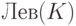 - это все то, что может появляться в правых выводах левее любого вхождения нетерминала K.
- это все то, что может появляться в правых выводах левее любого вхождения нетерминала K.
Решение. Продолжив построение правого вывода, все нетерминалы справа от K можно заменить на терминалы (а слева от K при этом ничего не изменится).
16.1.6.
Построить грамматику, содержащую для каждого нетерминала K исходной грамматики нетерминал  , причем следующее свойство должно выполняться для любого нетерминала K исходной грамматики: в новой грамматике из
, причем следующее свойство должно выполняться для любого нетерминала K исходной грамматики: в новой грамматике из  выводимы все элементы
выводимы все элементы 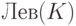 и только они. (При этом терминалы и нетерминалы исходной грамматики являются терминалами новой.)
и только они. (При этом терминалы и нетерминалы исходной грамматики являются терминалами новой.)
Решение. Пусть P - начальный нетерминал грамматики. Тогда в новой грамматике будет правило
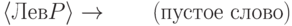
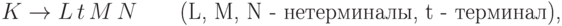
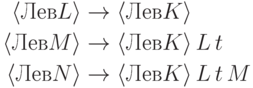
16.1.7. Почему в предыдущей задаче важно, что мы рассматриваем только правые выводы?
Ответ. В противном случае следовало бы учитывать преобразования, происходящие внутри слова, стоящего слева от K.
16.1.8.
Для данной грамматики построить алгоритм, который по любому
слову выясняет, каким из множеств 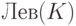 оно принадлежит.
оно принадлежит.
(Замечание для знатоков. Существование такого алгоритма - и даже конечного автомата, то есть индуктивного расширения с конечным числом значений, см. "раздел 1.3." , - вытекает из предыдущей задачи, так как построенная в ней грамматика имеет специальный вид: в правых частях всего один нетерминал, причем он стоит у левого края. Тем не менее мы приведем явное построение.)
Решение. Будем называть ситуацией данной грамматики одно из ее правил, в правой части которого отмечена одна из позиций (до первой буквы, между первой и второй буквой, 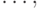 после последней буквы). Например, правило
после последней буквы). Например, правило
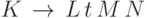
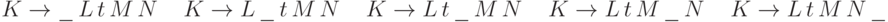
Будем говорить, что слово S согласовано с ситуацией 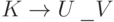 , если S кончается на U, то есть
, если S кончается на U, то есть 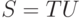 при некотором T, и, кроме того, T принадлежит
при некотором T, и, кроме того, T принадлежит 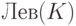 . (Смысл этого определения примерно таков: в стеке S подготовлена часть U для будущей свертки UV в K.) В этих терминах
. (Смысл этого определения примерно таков: в стеке S подготовлена часть U для будущей свертки UV в K.) В этих терминах 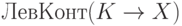 - это множество всех слов,
согласованных с ситуацией
- это множество всех слов,
согласованных с ситуацией 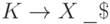 ,,
а
,,
а 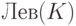 - это множество всех слов, согласованных с ситуацией
- это множество всех слов, согласованных с ситуацией 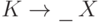 (где
(где  - любое правило для нетерминала K ).
- любое правило для нетерминала K ).
Эквивалентное определение в терминах LR-процесса: S согласовано с ситуацией 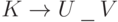 , если существует успешный LR-процесс, в котором события развиваются так:
, если существует успешный LR-процесс, в котором события развиваются так:
- в ходе процесса в стеке появляется слово S, и оно оканчивается на U ;
- некоторое время S не затрагивается, а справа от него появляется V ;
- UV сворачивается в K ;
- процесс продолжается и успешно завершается.
16.1.9. Доказать эквивалентность этих определений.
Указание.
Если 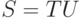 и T принадлежит
и T принадлежит 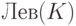 , то можно получить в стеке сначала T, потом U, потом V, потом свернуть UV в K и затем успешно завершить процесс. (Мы используем несколько раз тот факт, что из любого нетерминала что-то да выводится: благодаря этому мы можем добавить в стек любое слово.)
, то можно получить в стеке сначала T, потом U, потом V, потом свернуть UV в K и затем успешно завершить процесс. (Мы используем несколько раз тот факт, что из любого нетерминала что-то да выводится: благодаря этому мы можем добавить в стек любое слово.)
Наша цель - построение алгоритма, распознающего
принадлежность произвольного слова к 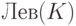 .
Рассмотрим функцию, сопоставляющую с каждым словом S
(из терминалов и нетерминалов) множество всех согласованных
с ним ситуаций. Это множество назовем состоянием, соответствующим слову S }. Будем обозначать его
.
Рассмотрим функцию, сопоставляющую с каждым словом S
(из терминалов и нетерминалов) множество всех согласованных
с ним ситуаций. Это множество назовем состоянием, соответствующим слову S }. Будем обозначать его  . Достаточно показать, что функция
. Достаточно показать, что функция  индуктивна, то есть что значение
индуктивна, то есть что значение 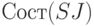 , где J - терминал или нетерминал, может быть вычислено, если известно
, где J - терминал или нетерминал, может быть вычислено, если известно  и символ J. (Мы видели
ранее, как принадлежность к
и символ J. (Мы видели
ранее, как принадлежность к 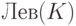 выражается в терминах этой функции.) Значение
выражается в терминах этой функции.) Значение 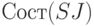 вычисляется по таким правилам:
вычисляется по таким правилам:
(1) Если слово S согласовано с ситуацией K->U_V, причем слово V начинается на букву J, то есть V=JW, то SJ согласовано с ситуацией K->UJ_W.
Это правило полностью определяет все ситуации с непустой
левой половиной (то есть не начинающиеся с подчеркивания),
согласованные с SJ. Осталось определить, для каких
нетерминалов K слово SJ принадлежит 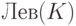 . Это делается по двум правилам:
. Это делается по двум правилам:
(2) Если ситуация L->U_V согласована с SJ (согласно правилу (1)), а V начинается на нетерминал K, то SJ принадлежит Лев(K).
(3) Если SJ входит в Лев(L) для некоторого L, причем L->V - правило грамматики и V начинается на нетерминал K, то SJ принадлежит Лев(K).
Заметим, что правило (3) можно рассматривать как аналог
правила (2): в указанных в (3) предположениях ситуация 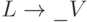 согласована с SJ, а V начинается на нетерминал K.
согласована с SJ, а V начинается на нетерминал K.
Корректность этих правил в общем-то очевидна, если
хорошенько подумать. Единственное, что требует некоторых
пояснений - это то, почему с помощью правил (2) и (3)
обнаружатся  терминалы K, для которых SJ принадлежит
терминалы K, для которых SJ принадлежит 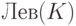 . Попытаемся это объяснить. Рассмотрим правый вывод, в котором SJ стоит слева от K.
Откуда мог взяться в нем нетерминал K? Если правило, которое его породило, породило также и конец слова SJ, то
принадлежность SJ к
. Попытаемся это объяснить. Рассмотрим правый вывод, в котором SJ стоит слева от K.
Откуда мог взяться в нем нетерминал K? Если правило, которое его породило, породило также и конец слова SJ, то
принадлежность SJ к 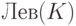 будет обнаружена по правилу (2). Если же K было первой буквой слова, порожденного каким-то другим нетерминалом L, то - благодаря правилу (3) - достаточно установить принадлежность SJ к
будет обнаружена по правилу (2). Если же K было первой буквой слова, порожденного каким-то другим нетерминалом L, то - благодаря правилу (3) - достаточно установить принадлежность SJ к 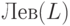 . Осталось применить те же рассуждения к L и так далее.
. Осталось применить те же рассуждения к L и так далее.
В терминах LR-процесса то же самое можно сказать так. Сначала нетерминал K может участвовать в нескольких свертках, не затрагивающих SJ (они соответствуют применению правила (3)), но затем он обязан подвергнуться свертке, затрагивающей SJ (что соответствует применению правила (2)).
Осталось выяснить, какие ситуации согласованы с пустым
словом, то есть для каких нетерминалов K пустое слово
принадлежит 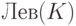 . Это определяется по следующим правилам:
. Это определяется по следующим правилам:
- начальный нетерминал таков;
- если K таков и K -> V - правило грамматики, причем слово V начинается с нетерминала L, то и L таков.
16.1.10. Проделать описанный анализ для грамматики

Решение. Множества Сост(S) для различных S приведены в таблице (см. ниже).
| Слово S | Сост (S) |
|---|---|
| пустое |
E->_E+T E->_T T->_T*F T->_F F->_x F->_(E) |
| E | E->E_+T |
| T | E->T_ T->T_*F |
| F | T->F_ |
| x | F->x_ |
| ( |
F->(_E) E->_E+T E->_T T->_T*F T->_F F->_x F->_(E) |
| E+ |
E->E+_T T->_T*F T->_F F->_x F->_(E) |
| T* | T->T*_F F->_x F->_(E) |
| (E | F->(E_) E->E_+T |
| (T | =T |
| (F | =F |
| (x | =x |
| (( | =( |
| E+T | E->E+T_ T->T_*F |
| E+F | =F |
| E+x | =x |
| E+( | =( |
| T*F | T->T*F |
| T*x | =x |
| T*( | =( |
| (E) | F->(E)_ |
| (E+ | =E+ |
| E+T* | =T* |
Знак равенства означает, что множества ситуаций, являющиеся
значениями функции  на словах, стоящих слева и справа от знака равенства, одинаковы.
на словах, стоящих слева и справа от знака равенства, одинаковы.
Правило определения 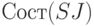 , если известны
, если известны  и J (здесь S - слово из терминалов и нетерминалов, J - терминал или нетерминал), таково:
и J (здесь S - слово из терминалов и нетерминалов, J - терминал или нетерминал), таково:
надо найти Сост(S) в правой колонке, взять соответствующее ему слово T в левой колонке, приписать к нему J и взять множество, стоящее напротив слова TJ (если слово TJ в таблице отсутствует, то Сост(SJ) пусто).
