Представление множеств. Хеширование
13.1. Хеширование с открытой адресацией
В
"лекции 6"
было указано несколько представлений для множеств,
элементами которых являются целые числа произвольной
величины. Однако в любом из них хотя бы одна из операций
проверки принадлежности, добавления и удаления элемента
требовала количества действий, пропорционального числу
элементов множества. На практике это бывает слишком много.
Существуют способы, позволяющие получить для всех трех
упомянутых операций оценку  . Один из таких
способов мы рассмотрим в следующей лекции. В этой лекции мы
разберем способ, которые хотя и приводит к
. Один из таких
способов мы рассмотрим в следующей лекции. В этой лекции мы
разберем способ, которые хотя и приводит к 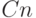 действиям
в худшем случае, но зато "в среднем" требует
значительно меньшего их числа. (Мы не будем уточнять слов
"в среднем", хотя это и можно сделать.) Этот
способ называется хешированием.
действиям
в худшем случае, но зато "в среднем" требует
значительно меньшего их числа. (Мы не будем уточнять слов
"в среднем", хотя это и можно сделать.) Этот
способ называется хешированием.
Пусть нам необходимо представлять множества элементов
типа T, причем число элементов в них заведомо
меньше n. Выберем некоторую функцию h, определенную
на значениях типа T и принимающую значения 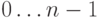 . Было бы хорошо, чтобы эта функция
принимала на элементах будущего множества по возможности
более разнообразные значения. (Худший случай - это когда ее
значения на всех элементах хранимого множества одинаковы.)
Эту функцию будем называть хеш-функцией, или,
как еще говорят, функцией расстановки.
. Было бы хорошо, чтобы эта функция
принимала на элементах будущего множества по возможности
более разнообразные значения. (Худший случай - это когда ее
значения на всех элементах хранимого множества одинаковы.)
Эту функцию будем называть хеш-функцией, или,
как еще говорят, функцией расстановки.
Введем два массива
val: array [0..n-1] of T; used: array [0..n-1] of boolean;
(мы позволяем себе писать n-1 в качестве границы
в определении типа, хотя в паскале это не разрешается).
В этих массивах будут храниться элементы множества: оно
равно множеству всех ![{val}\,{[i]}](/sites/default/files/tex_cache/b4fec4da189a8b854f5414416cf02f19.png) для тех i, для
которых
для тех i, для
которых ![{used}\,{[i]}](/sites/default/files/tex_cache/cf32e9c5c5c40209b2f92392cff171fd.png) , причем все эти
, причем все эти ![{val}\,{[i]}](/sites/default/files/tex_cache/b4fec4da189a8b854f5414416cf02f19.png) различны. По возможности мы будем
хранить элемент t на месте h(t), считая это место "исконным" для элемента t.
Однако может случиться так, что новый элемент, который мы
хотим добавить, претендует на уже занятое место (для
которого used истинно). В этом случае мы отыщем
ближайшее справа свободное место и запишем элемент туда.
("Справа" значит "в сторону увеличения
индексов"; дойдя до края, мы перескакиваем в начало.) По
предположению, число элементов всегда меньше n, так что
пустые места заведомо будут.
различны. По возможности мы будем
хранить элемент t на месте h(t), считая это место "исконным" для элемента t.
Однако может случиться так, что новый элемент, который мы
хотим добавить, претендует на уже занятое место (для
которого used истинно). В этом случае мы отыщем
ближайшее справа свободное место и запишем элемент туда.
("Справа" значит "в сторону увеличения
индексов"; дойдя до края, мы перескакиваем в начало.) По
предположению, число элементов всегда меньше n, так что
пустые места заведомо будут.
Формально говоря, в любой момент должно соблюдаться такое требование: для любого элемента множества участок справа от его исконного места до его фактического места полностью заполнен.
Благодаря этому проверка принадлежности заданного элемента t
осуществляется легко: встав на h(t), двигаемся
направо, пока не дойдем до пустого места или до элемента t. В первом
случае элемент t отсутствует в множестве, во втором - присутствует. Если
элемент отсутствует, то его можно добавить
на найденное пустое место. Если присутствует, то можно его
удалить (положив 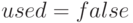 ).
).
13.1.1. В предыдущем абзаце есть ошибка. Найти ее и исправить.
Решение. Дело в том, что при удалении требуемое свойство "отсутствия пустот" может нарушиться. Поэтому будем делать так. Создав дыру, будем двигаться направо, пока не натолкнемся на элемент, стоящий не на исконном месте, или на еще одно пустое место. Во втором случае на этом можно успокоиться. В первом случае посмотрим, не нужно ли найденный элемент поставить на место дыры. Если нет, то продолжаем поиск, если да, то затыкаем им старую дыру. При этом образуется новая дыра, с которой делаем все то же самое.
13.1.2. Написать программы проверки принадлежности, добавления и удаления.
Решение.
function принадлежит (t: T): boolean;
| var i: integer;
begin
| i := h (t);
| while used [i] and (val [i] <> t) do begin
| | i := (i + 1) mod n;
| end; {not used [i] or (val [i] = t)}
| принадлежит := used [i] and (val [i] = t);
end;procedure добавить (t: T);
| var i: integer;
begin
| i := h (t);
| while used [i] and (val [i] <> t) do begin
| | i := (i + 1) mod n;
| end; {not used [i] or (val [i] = t)}
| if not used [i] then begin
| | used [i] := true;
| | val [i] := t;
| end;
end;
procedure исключить (t: T);
| var i, gap: integer;
begin
| i := h (t);
| while used [i] and (val [i] <> t) do begin
| | i := (i + 1) mod n;
| end; {not used [i] or (val [i] = t)}
| if used [i] and (val [i] = t) then begin
| | used [i] := false;
| | gap := i;
| | i := (i + 1) mod n;
| | {gap - дыра, которая может закрыться одним из i,i+1,...}
| | while used [i] do begin
| | | if i = h (val[i]) then begin
| | | | {на своем месте, ничего не делать}
| | | end else if dist(h(val[i]),i) < dist(gap,i) then begin
| | | | {gap...h(val[i])...i, ничего не делать}
| | | end else begin
| | | | used [gap] := true;
| | | | val [gap] := val [i];
| | | | used [i] := false;
| | | | gap := i;
| | | end;
| | | i := (i + 1) mod n;
| | end;
| end;
end;Здесь 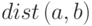 - измеренное по часовой стрелке
(слева
направо) расстояние от a до b, то есть
- измеренное по часовой стрелке
(слева
направо) расстояние от a до b, то есть
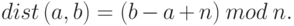
13.1.3.
Существует много вариантов хеширования. Один из них таков:
обнаружив, что исконное место (обозначим его  ) занято, будем
искать свободное не среди
) занято, будем
искать свободное не среди 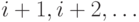 , а среди
, а среди 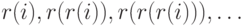 , где
, где  - некоторое отображение
- некоторое отображение 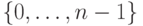 в себя. Какие при этом будут трудности?
в себя. Какие при этом будут трудности?
Ответ. (1) Не гарантируется, что если пустые места есть, то
мы их найдем. (2) При удалении неясно, как заполнять дыры. (На
практике во многих случаях удаление не нужно, так что такой
способ также применяется. Считается, что удачный подбор функции  может предотвратить образование "скоплений" занятых
ячеек.)
может предотвратить образование "скоплений" занятых
ячеек.)
13.1.4. Пусть для хранения множества всех правильных русских слов в программе проверки орфографии используется хеширование. Что нужно добавить, чтобы к тому же уметь находить английский перевод любого правильного слова?
Решение. Помимо массива val, элементы которого являются русскими словами, нужен параллельный массив их английских переводов.
