Интернет-Университет Суперкомпьютерных Технологий:

Параллельное программирование
[+]
Опубликован: 22.12.2006 | Доступ: свободный | Студентов: 1244 / 139 | Оценка: 4.73 / 4.45 | Длительность: 18:17:00
ISBN: 978-5-94774-546-7
Темы: Программирование, Суперкомпьютерные технологии
Специальности: Программист
Лекция 7:

Параллельное программирование — аппарат исследования операций
A
|
версия для печати
< Лекция 6 || Лекция 7: 123456 || Лекция 8 >

Нижняя оценка минимального числа процессоров, необходимого для выполнения алгоритма за заданное время

Алгоритм 5.

  1. Первоначально полагаем n = 0.

  2. Организуем перебор всех отрезков [\theta _{1}, \theta _{2}] \subseteq [0, T] в порядке

    \begin{align*} &[0,1] ;\\ &[0,2] ; [1,2] ;\\ &[0,3] ; [1,3] ; [2,3] ;\\ &. . . . . . . . . . . . . . . . . . . . . . . . . .\\ &[0,T] ; [1,T] ; \ldots , [T-1,T] . \end{align*}

    Всего таких отрезков T(T+1)/2.

  3. Для очередного анализируемого отрезка времени [\theta _{1},\theta _{2}] находим значение
    \begin{align*} n'= \left]\frac{\varphi^{(T^*)}(\theta_1,\theta_2)}{\theta_2 - \theta_1}\right[ . \end{align*}
  4. Если n' > n, выполняем операцию n := n'. После перебора всех отрезков окажется найденным значение n, которое равно максимальному из значений, удовлетворяющих (7.2).

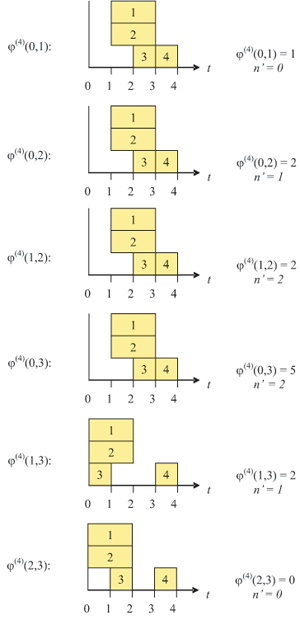
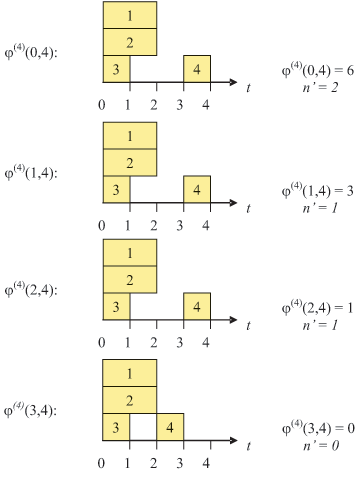
Пример. Нахождение оценки n.

Нахождение 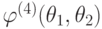\varphi ^{(4)}(\theta _{1},\theta _{2}) будем иллюстрировать графически, возможными временными диаграммами (рис. 7.19).

Нахождение нижней оценки числа исполнителей

увеличить изображение
Рис. 7.19. Нахождение нижней оценки числа исполнителей
Окончание

Рис. 7.19. Окончание

В результате анализа всех отрезков находим n = max n' = 2.

Нижняя оценка минимального времени выполнения данного алгоритма на ВС

Алгоритм 6.

  1. Первоначально полагаем

    \begin{align*} T = \max \left \{ ]\frac{1}{n}\sum_{j=1}^m t_j[,\,T_\t{кр}\right \}. \end{align*}

  2. Организуем перебор всех отрезков [\theta _{1}, \theta _{2}] \subseteq [0, T] в той же последовательности, что и в предыдущем алгоритме. (В процессе выполнения данного алгоритма значение T может увеличиваться, что при данном порядке перебора не приведёт к усложнению алгоритма.)

  3. Для очередного анализируемого отрезка времени [\theta _{1},\theta _{2}] находим значение

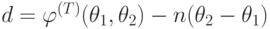
    d = \varphi ^{(T)}(\theta _{1},\theta _{2}) - n(\theta _{2} - \theta _{1})

  4. Если d > 0, выполняем операцию T := T + ] d/n [.
  5. Полагаем \tau _{2j}(T) := \tau _{2j}(T) + ] d/n [ , j = 1 , \dots ,m.

После перебора всех отрезков [\theta _{1}, \theta _{2}] окажется найденным окончательное значение T — нижняя оценка минимального времени выполнения данного алгоритма на данной ВС.

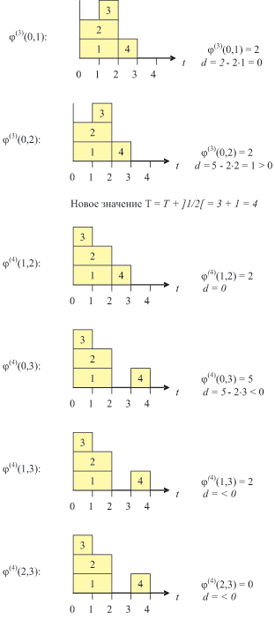
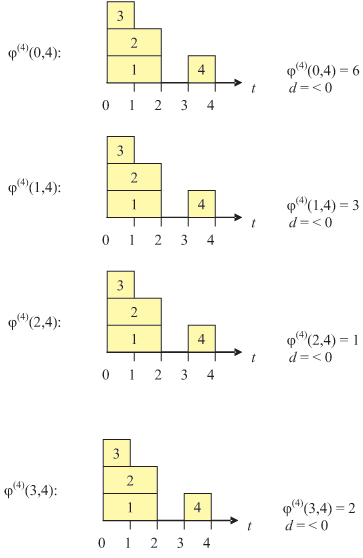
Пример. Произведём оценку T для графа G, рассмотренного в предыдущем примере, и ВС, состоящей из двух процессоров, n = 2 (рис. 7.20).

Оценка снизу минимального времени выполнения работ

увеличить изображение
Рис. 7.20. Оценка снизу минимального времени выполнения работ
Окончание

Рис. 7.20. Окончание

Первоначально находим

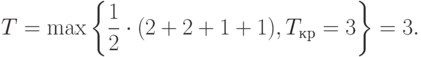
T = \max \left \{ \frac{1}{2}\cdot (2+2+1+1),T_{кр}=3\right \}=3.

После перебора всех отрезков, с учётом уточнения оценки времени в процессе этого перебора, окончательно находим T = 4.

Дальше >>
< Лекция 6 || Лекция 7: 123456 || Лекция 8 >

Вопросы и ответы

вопросов: 0