НОУ ИНТУИТ | Параллельное программирование. Лекция 7: Параллельное программирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.12.2006 | Доступ: свободный | Студентов: 1222 / 123 | Оценка: 4.73 / 4.45 | Длительность: 18:17:00

ISBN: 978-5-94774-546-7

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 13 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

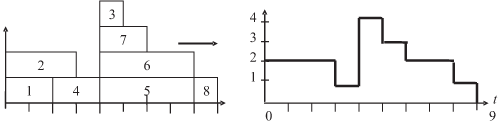
Определение 7. Функцию

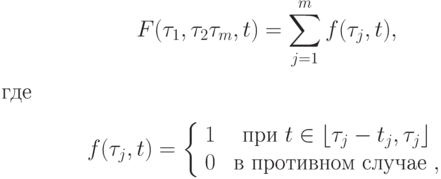
$\begin{align*} F(\tau_1,\tau_2 \dts \tau_m,t) = \sum_{j=1}^m f(\tau_j,t), \end{align*} где \begin{align*} f(\tau_j,t)= \left\{ \begin{array}{rcl} 1 &\text{ при } t \in \lfloor \tau_j - t_j,\tau_j\rfloor \\ 0 &\text{ в противном случае }, \end{array} \right. \end{align*}$

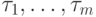назовём плотностью загрузки, найденной для значений $\tau _{1} , \dots ,\tau _{m}$ .

Для заданных 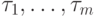$\tau _{1} , \dots , \tau _{m}$ значение функции F в каждый момент времени t совпадает с числом одновременно (параллельно) выполняющихся в этот момент работ.

Например, по диаграмме на 7.11, т.е. для 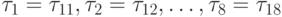$\tau _{1} = \tau _{11}, \tau _{2} = \tau _{12}, \dots , \tau _{8} = \tau _{18}$ , функция F(2, 3, 3, 4, 7, 8, 6, 9, t) имеет вид, представленный на рис. 7.13а. Для допустимого расписания, определяемого набором значений $\tau _{1} = 2,\tau _{2} = 4, \tau _{3} = 3, \tau _{4} = 4, \tau _{5} = 8, \tau _{6} = 9, \tau _{7} = 7$ , $\tau _{8} = 10$ , функция F(2, 4, 3, 4, 8, 9, 7, 10, t) имеет вид, представленный на рис. 7.13б.

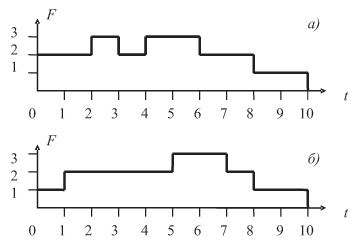
Рис. 7.13. Графики функции: а — для ранних сроков окончания работ,,б — для некоторого допустимого расписания

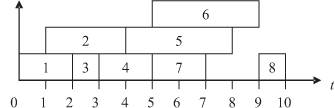
Для графического представления функции F удобно пользоваться временной диаграммой, которая для второго случая, например, имеет вид, представленный на рисунке 7.14..

Рис. 7.14. Временная диаграмма функции F

Пусть данный граф G, в котором учтены транзитивные связи, образует l полных множеств взаимно независимых работ (ПМВНР). (Каждая пара таких множеств может иметь непустое пересечение.) Обозначим r_i, i = 1 , ... , l, число работ, образующих i -е полное множество и найдём

R = max {r₁ , ... , r_l}.

Тогда

$\begin{align*} R = \max\limits_{\tau_1,\tau_2 \dts \tau_m} F(\tau_1,\ldots \tau_m, t), \end{align*}$

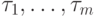т.к. возможно и такое распределение выполняемых работ во времени, задаваемое набором $\tau _{1} , \dots , \tau _{m}$ , (т.е. допустимое расписание), когда на каком-то отрезке времени выполняются все работы, составляющие ПМВНР с числом R работ.

Например, для графа на рис. 7.1 мы нашли ПМВНР {3,5,6,7}, включающее четыре работы. Тогда существует допустимое расписание, например, 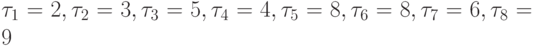$\tau _{1} = 2, \tau _{2} = 3, \tau _{3} = 5, \tau _{4} = 4, \tau _{5} = 8, \tau _{6} = 8, \tau _{7} = 6, \tau _{8} = 9$ такое, при котором максимальное значение плотности загрузки F равно четырём (рис. 7.15).

Рис. 7.15. Максимальное значение плотности загрузки

Таким образом, справедливо утверждение

Лемма. Минимальное число n процессоров одинаковой специализации и производительности (т.е. в однородной ВС), способных выполнить данный алгоритм за время T >= T_кр, не превышает R = max {r₁ , ... , r_l }, где r_i , i = 1 , ... , l, — число работ, входящих в i -е ПМВНР, которое составлено по взвешенному графу G, соответствующему этому алгоритму.

Определение 8. Функцию

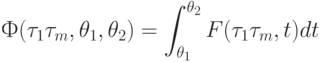
$\begin{align*} \text{Ф} (\tau_1 \dts \tau_m, \theta_1, \theta_2)= \int_{\theta_1}^{\theta_2} F(\tau_1 \dts \tau_m,t)dt \end{align*}$

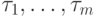назовём загрузкой отрезка $[\theta _{1}, \theta _{2}] \subset [0,T]$ для заданного допустимого расписания $\tau _{1}, \dots ,\tau _{m}$ .

Функция Ф определяет объём работ (суммарное время их выполнения) на фиксированном отрезке их выполнения при заданном допустимом расписании.

Так, для отрезка времени $[0, 4] \subset [0, 10]$ на рис. 7.13а Ф = 10 ; для отрезка времени [1, 3] на ррис. 7.13б Ф= 4 ; для отрезка времени [2, 5] на рис. 7.15 Ф = 10 и т.д.

Определение 9. Функцию

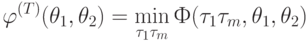
$\begin{align*} \varphi^{(T)} (\theta_1, \theta_2)= \min_{\tau_1 \dts \tau_m}\text{Ф} (\tau_1 \dts \tau_m, \theta_1, \theta_2) \notag \end{align*}$

назовём минимальной загрузкой отрезка $[\theta _{1}, \theta _{2}] \subset [0,T]$ .

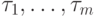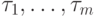Функция определяет минимально возможный объём работ, который при данном T и при различных допустимых значениях (расписаниях) $\tau _{1} , \dots , \tau _{m}$ должен быть выполнен на отрезке времени $[\theta _{1}, \theta _{2}]\subset [0, T]$ . Это означает, что как бы мы не планировали вычислительный процесс, который должен быть закончен к моменту времени T, т.е. 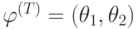какой бы набор значений $\tau _{1} , \dots , \tau _{m}$ мы не выбрали, объём работ, выполняемых на отрезке времени $[\theta _{1}, \theta _{2}]$ , не может быть меньше значения $\varphi ^{(T)} = (\theta _{1},\theta _{2})$ .

Теорема 1. Для того чтобы T было наименьшим временем выполнения данного алгоритма однородной вычислительной системой, состоящей из n процессоров, либо чтобы n процессоров было достаточно для выполнения данного алгоритма за время T, необходимо, чтобы для данного отрезка времени $[\theta _{1}, \theta _{2}] \subset [0, T]$ выполнялось соотношение

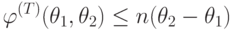$\begin{align*} \varphi^{(T)}(\theta_1, \theta_2) \le n ( \theta_2 - \theta_1) \notag \end{align*}$

( 7.1)

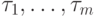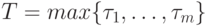Доказательство. Нетрудно видеть, что если при данном наборе $\tau _{1} , \dots , \tau _{m}$ — сроках окончания выполнения работ, в том числе и при таком наборе, при котором обеспечивается минимальное или заданное $T = max \{ \tau _{1}, \dots , \tau _{m}\}$ , для реализации алгоритма достаточно n процессоров, то

$\begin{align*} \max_{t\in[0,T]}F(\tau_1 \dts \tau_m\,t)\le n. \end{align*}$

Отсюда, для любого отрезка времени $[\theta _{1}, \theta _{2}] \subset [0,T]$

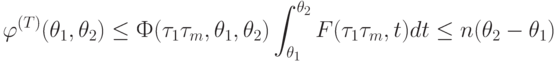
$\begin{align*} \varphi^{(T)}(\theta_1, \theta_2)\le \text{Ф} (\tau_1 \dts \tau_m, \theta_1, \theta_2) \int_{\theta_1}^{\theta_2} F(\tau_1 \dts \tau_m,t)dt \le n ( \theta_2 - \theta_1) \end{align*}$

что и требовалось доказать.

Необходимость, но не достаточность условия (7.1) покажем на примере. Пусть алгоритму соответствует граф G на рис. 7.16а. Пусть T=3, и одна из возможных диаграмм выполнения алгоритма — на рис. 7.16б.

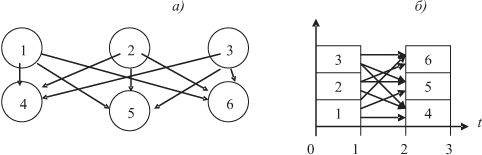
Рис. 7.16. Пример: минимальная плотность загрузки не соответствует действительной: а — информационный граф, б — временная диаграмма загрузки

Оценим на основе (7.1) число n процессоров, достаточное для выполнения алгоритма в указанное время. Из (7.1) имеем общее соотношение

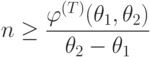$\begin{align*} n\ge \frac{\varphi^{(T)}(\theta_1, \theta_2)}{\theta_2 - \theta_1} \notag \end{align*}$

( 7.2)

Для получения полной оценки надо перебрать все отрезки $[\theta _{1},\theta _{2}] \subset [0, T]$ т.е.

$\begin{align*} n\ge \max_{[\theta_1, \theta_2] \subset [0, T]}\frac{\varphi^{(T)}(\theta_1, \theta_2)}{\theta_2 - \theta_1} \notag \end{align*}$

( 7.3)

Проанализируем все возможные отрезки $[\theta _{1}, \theta _{2}] \subset [0,3] : \varphi ^{(3)}(0, 1) = \varphi ^{(3)}(1, 2) \varphi ^{(3)}(2, 3) = 0, \varphi ^{(3)}(0, 2) = \varphi ^{(3)}(1, 3)= 3, \varphi ^{(3)}(0, 3) = 6$ . Находим минимальное n = 2, удовлетворяющие (7.3). Однако из рисунка видно, что не существует плана выполнения работ на двух процессорах за время T=3. Минимально достаточное число процессоров здесь n = 3.

Функция $\varphi ^{(T)}(\theta _{1}, \theta _{2})$ минимальной загрузки отрезка времени является одним из основных средств оценки предпринимаемых действий при решении задач распараллеливания. Поэтому ниже будет дан алгоритм нахождения её значения.

Предварительно определим функцию

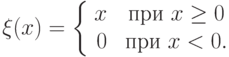
$\begin{align*} \xi (x) = \left\{ \begin{array}{rcl} x &\text { при } x\ge 0 \\ 0 &\text { при } x< 0. \end{array} \right. \end{align*}$

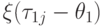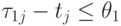Тогда значение $\xi (\tau _{1j} - \theta _{1})$ характеризует условный объём части работы j на отрезке времени $[\theta _{1}, \theta _{2}]$ при условии $\tau _{1j} - t_{j} \le \theta _{1}$ и при максимальном смещении времени выполнения работы j влево (рис. 7.17а).

Значение 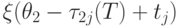$\xi (\theta _{2} - \tau _{2j}(T) + t_{j})$ характеризует аналогичный объём работы j при максимальном смещении времени выполнения работы j вправо. Это соответствует, например, ситуации, изображённой на рис. 7.17б.

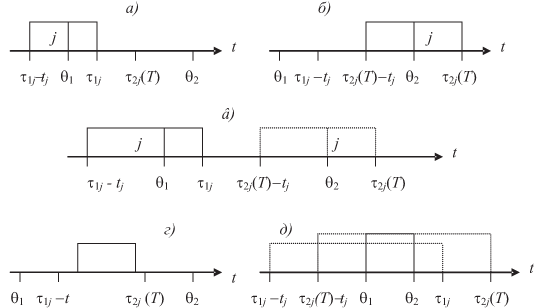
Рис. 7.17. Нахождение минимальной плотности загрузки отрезка: все различные случаи соотношения времени выполнения работ и сроков

Если для работы j оба указанных выше значения функции $\xi$ отличны от нуля, но не превышают значение t_j и $\theta _{2} - \theta _{1}$ , то максимально разгрузить отрезок $[\theta _{1}, \theta _{2}]$ от работы j можно смещением времени его выполнения в сторону, обеспечивающую меньшее из двух указанных выше значений $\xi$ (рис. 7.17в).

Существуют два случая, когда работа j не может быть хотя бы частично смещена с отрезка $[\theta _{1}, \theta _{2}]:$

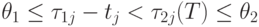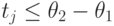а) $\theta _{1} \le \tau _{1j} - t_{j} < \tau _{2j} (T) \le \theta _{2}$ , в этом случае очевидно, что $t_{j} \le \theta _{2} - \theta _{1}$ (рис. 7.17г), и объём работы j, выполняемой на отрезке, совпадает с объёмом t_j всей этой работы;

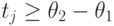б) $\tau _{1j} \ge \theta _{2} \Lambda \tau _{2j}(T) - t_{j} \le \theta _{1}$ , в этом случае очевидно, что $t_{j} \ge \theta _{2} - \theta _{1}$ (рис. 7.17д), и объём части работы j, выполняемой на отрезке $[\theta _{1}, \theta _{2}]$ совпадает со значением $\theta _{2} - \theta _{1}$ .

Приведённый ниже алгоритм объединяет все возможные указанные выше случаи.

Алгоритм 4 нахождения значения функции $\varphi ^{(T)}(\theta _{1}, \theta _{2})$ .

1. Предполагаем, что для каждой работы j = 1, ... , m, известны значения 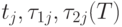$t_{j},\tau _{1j}, \tau _{2j}(T)$ . Полагаем равным нулю значение переменной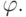 $\phi.$

2. Организуем последовательный анализ работ j = 1, ... , m.

3. Для каждой работы j полагаем

$\varphi := \varphi + min \{ \xi (\tau _{1j} - \theta _{1}), \xi (\theta _{2} -\tau _{2j}(T) + t_{j}), t_{j} , \theta _{2} - \theta _{1}\}$ .

После перебора всех работ $\varphi = \varphi ^{(T)}(\theta _{1},\theta _{2})$ .

Конец алгоритма.

Выше было получено соотношение (7.2) , которое можно использовать для нижней оценки количества n процессоров, необходимых для выполнения данного алгоритма за время, не превышающее T.

Приведём аналогичное соотношение для нижней оценки минимального времени Т.

Теорема 2. Пусть заданный алгоритм выполняется на ВС, состоящей из n процессоров, и T^* — текущее значение оценки снизу времени выполнения алгоритма. Пусть на отрезке времени $[\theta _{1}, \theta _{2}] \subset [0, T^{*}]$ выполняется соотношение

$\varphi ^{(T*)}(\theta _{1},\theta _{2}) - n(\theta _{2} - \theta _{1}) = d > 0$ .

Тогда минимальное время T выполнения алгоритма удовлетворяет соотношению

$\begin{align*} T \ge T^* + \frac{d}{n}. \end{align*}$

( 7.4)

Теоремы 1 и 2 на основе анализа такой локальной характеристики параллельного алгоритма, как значение функции $\phi$ минимальной загрузки отрезка, предлагают способы оценки снизу ресурсов, необходимых для реализации каждого заданного алгоритма:

числа n процессоров при заданном ограничении на длительность T процесса;
минимального времени T, необходимого для реализации данного алгоритма при заданном числе n процессоров.

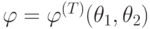Рис. 7.18. К примеру нахождения нижней оценки числа исполнителей

Дальше >>

Параллельное программирование

Параллельное программирование — аппарат исследования операций

Вопросы и ответы

Авторизоваться

Параллельное программирование

Параллельное программирование — аппарат исследования операций

Вопросы и ответы