НОУ ИНТУИТ | Параллельное программирование. Лекция 7: Параллельное программирование

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 22.12.2006 | Доступ: свободный | Студентов: 1234 / 134 | Оценка: 4.73 / 4.45 | Длительность: 18:17:00

ISBN: 978-5-94774-546-7

Темы: Программирование, Суперкомпьютерные технологии

Специальности: Программист

|

Вам нравится? Нравится 13 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Временные оценки на информационных графах

Информационный граф отображает порядок следования работ. Тогда очевидно, что момент окончания выполнения любой работы (если началом отсчёта времени является момент начала выполнения работ — начало выполнения алгоритма) не может быть меньше максимальной из длин всех путей, которые заканчиваются вершиной, соответствующей этой работе.

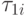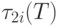Таким образом, для каждой i = 1 , ... , m работы алгоритма, представленного информационным графом, можно найти ранний срок $\tau _{1i}$ окончания её выполнения. Если же выполнение алгоритма ограничено временем T < T_кр, то для каждой работы можно найти и поздний срок $\tau _{2i}(T)$ окончания её выполнения. Окончание выполнения i -й работы позже этого срока приводит к тому, что выполнение других работ, следующих за данной, не может быть закончено до истечения времени T. Иначе говоря, поздний срок окончания выполнения данной работы не может превышать разности между значением T и максимальной из длин путей, в первую вершину которых входит дуга, что исходит из вершины, соответствующей данной работе. Без задания значения T (ограничения на длительность вычислительного процесса) определение позднего срока окончания выполнения работы не имеет смысла.

При T = T_кр ранние сроки окончания выполнения работ, составляющих критические пути, совпадают с поздними сроками окончания их выполнения.

Прежде чем рассмотреть алгоритм нахождения ранних и поздних сроков окончания выполнения работ по расширенной матрице следования S^*, отметим, что учёт транзитивных связей увеличивает число необходимых действий. Так как граф G не содержит контуров, то матрица следования S может быть преобразована в треугольную. Однако при построении алгоритмов решения задач распараллеливания не представляется удобным преобразовывать матрицу следования. Поэтому будем считать, что в общем случае матрица S не треугольная.

Алгоритм 2 нахождения ранних сроков окончания выполнения работ.

Полагаем первоначально $\tau _{11} = \tau _{12} = \dots = \tau _{1m}= 0$ .
Производя циклический обзор строк матрицы S, находим очередную из необработанных строк. Если все строки обработаны, выполнение алгоритма заканчивается.
Пусть j — номер найденной необработанной строки. Если j -я строка не содержит единичных элементов, полагаем $\tau _{1j} = t_{j}$ . Переходим к выполнению шага 6.
Если j -я строка содержит единичные элементы, выбираем элементы множества 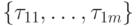$\{ \tau _{11} , \dots , \tau _{1m}\}$ , соответствующие номерам единичных элементов j -й строки.
Если все выбранные таким образом элементы, образующие множество 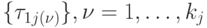$\{ \tau _{1j(\nu )}\} , \nu = 1, \dots , k_{j}$ , отличны от нуля, полагаем $\tau _{1}j = max \tau _{1 j\nu } + t_{j}$ .

Если хотя бы один из выбранных элементов нулевой (соответствующий ранний срок ещё не найден), выполняем шаг 2.
Обработанную j -ю строку метим, чтобы исключить её повторную обработку. Переходим к выполнению шага 2.

Примечание. Если граф G не содержит контуров, зацикливание при этом невозможно.

Конец алгоритма.

Если матрица S треугольная, то никогда не складываются условия для многократного циклического обзора строк. Тогда ранние сроки окончания выполнения работ находятся за один последовательный просмотр строк матрицы S.

Очевидно, что 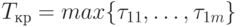$T_{кр} = max \{ \tau _{11} , \dots ,\tau _{1m}\}$ .

По матрице S^* ( S — треугольная) на рис. 7.5 (граф G — на рис. 7.1) находим

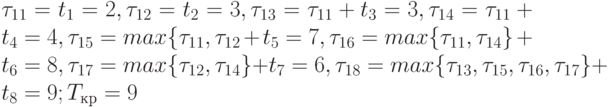$\tau _{11} = t_{1} = 2, \tau _{12} = t_{2} = 3, \tau _{13} = \tau _{11} + t_{3}=3, \tau _{14}= \tau _{11} + t_{4} = 4,\tau _{15} = max \{ \tau _{11}, \tau _{12} + t_{5}= 7, \tau _{16} = max\{ \tau _{11},\tau _{14}\} + t_{6} = 8, \tau _{17} = max \{ \tau _{12},\tau _{14} \} + t_{7} = 6,\tau _{18} = max \{ \tau _{13}, \tau _{15}, \tau _{16}, \tau _{17}\} + t_{8} = 9; T_{кр} = 9$ .

Чтобы рассмотреть пример с нетреугольной матрицей следования, выберем граф G без контуров с "неправильно" пронумерованными вершинами (рис. 7.10).

Рис. 7.10. Информационный граф с не треугольной матрицей следования

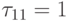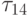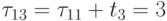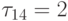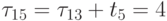После обработки первой строки $\tau _{11} = 1$ . Попытка обработать вторую строку неудачна, т.к. $\tau _{13}$ и $\tau _{14}$ ещё не найдены. После обработки третьей строки $\tau _{13} = \tau _{11} + t_{3} = 3$ . Обработка четвёртой строки даёт $\tau _{14} = 2$ . После обработки пятой строки $\tau _{15} = \tau _{13} + t_{5} = 4$ . Попытка обработки шестой строки неудачна, т.к. 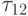не найдено значение $\tau _{12}$ . Приступаем к следующему циклу обзора необработанных строк S. Обрабатываем вторую строку: $\tau _{12} = max \{ \tau _{13}, \tau _{14}\} +t_{2} = 6$ . 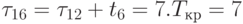После обработки шестой строки $\tau _{16} = \tau _{12} + t_{6} = 7.T_{кр} = 7$ .

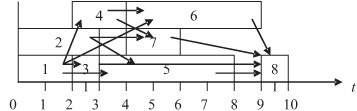
Для удобства представления наряду с другими способами будем пользоваться наглядными диаграммами выполнения работ при заданных значениях времени начала или окончания их выполнения. Работы обозначаются прямоугольниками с постоянной высотой и длиной, равной времени выполнения. Стрелки, связывающие прямоугольники-работы, соответствуют дугам в графе G. На рис. 7.11 представлена диаграмма выполнения работ, отраженных графом G на рис. 7.1 и расширенной матрицей следования на рис. 7.5 — при ранних сроках выполнения работ.

Рис. 7.11. Временная диаграмма выполнения работ при ранних сроках окончания

Алгоритм 3 нахождения поздних сроков окончания выполнения работ при заданном значении Т.

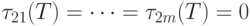Полагаем первоначально $\tau _{21}(T) = \dots = \tau _{2m}(T) =0$ .
Производя циклический обзор справа налево столбцов матрицы S, находим очередной из не обработанных ещё столбцов. Если все столбцы обработаны, выполнение алгоритма заканчивается.
Пусть j — номер найденного необработанного столбца. Если j -й столбец не содержит единичных элементов, полагаем 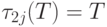$\tau _{2j}(T) = T$ . Переходим к выполнению шага 6.
Если j -й столбец содержит единичные элементы, выбираем элементы множества 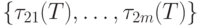$\{ \tau _{21}(T) , \dots ,\tau _{2m}(T) \}$ , соответствующие номерам единичных элементов j-го столбца.
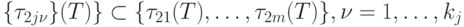Если все выбранные таким образом элементы $\{ \tau _{2j\nu }\} (T)\} \subset \{ \tau _{21}(T), \dots , \tau _{2m}(T)\} , \nu = 1 , \dots , k_{j}$ , отличны от нуля, полагаем

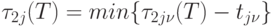$\tau _{2j} (T) = min \{ \tau _{2j\nu } (T) - t_{j\nu } \}$ .

В противном случае выполняем шаг 2.
Обработанный j -й столбец метим с целью исключения его повторной обработки. Переходим к выполнению шага 2.

Конец алгоритма.

Если матрица S — треугольная, то поздние сроки окончания выполнения работ находятся за один просмотр столбцов.

Для матрицы S^* (матрица S — треугольная) на рис. 7.5 и для T = 10 за один просмотр находим

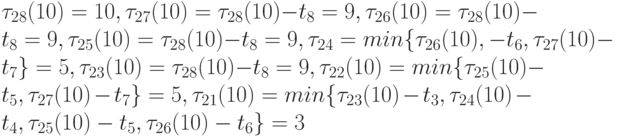$\tau _{28}(10) = 10, \tau _{27}(10) = \tau _{28}(10) - t_{8} = 9, \tau _{26}(10) = \tau _{28}(10)- t_{8} = 9, \tau _{25}(10) = \tau _{28}(10) - t_{8} = 9 ,\tau _{24} = min \{ \tau _{26}(10), - t_{6}, \tau _{27}(10) - t_{7}\} = 5, \tau _{23}(10) = \tau _{28}(10) - t_{8} = 9, \tau _{22}(10) = min \{ \tau _{25}(10) - t_{5},\tau _{27}(10) - t_{7} \} = 5, \tau _{21}(10) = min \{ \tau _{23}(10) - t_{3}, \tau _{24}(10) - t_{4},\tau _{25}(10) - t_{5}, \tau _{26}(10) - t_{6}\} = 3$ .

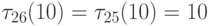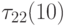Для нетреугольной матрицы S на рис. 7.10 при T = 10 находим $\tau _{26}(10) = \tau _{25}(10) = 10$ . Обработка четвёртого столбца откладывается, т.к. не найдено значение $\tau _{22}(10)$ . По этой же причине не обрабатывается третий столбец. После обработки второго столбца находим $\tau _{22}(10) = \tau _{26}(10)- t_{6} = 9$ .

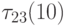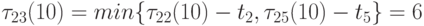Обработка первого столбца невозможна, т.к. ещё не найдено значение $\tau _{23}(10)$ . Продолжаем циклический обзор столбцов. После обработки четвёертого столбца получаем $\tau _{24}(10) = \tau _{22}(10) - t_{2} = 6$ . Обработка третьего столбца даёт $\tau _{23}(10) = min \{ \tau _{22}(10) - t_{2}, \tau _{25}(10) - t_{5}\} =6$ . После обработки первого столбца находим $\tau _{21}(10) = \tau _{23}(10) - t_{3} = 4$ .

Диаграммы выполнения работ при поздних сроках окончания, по графам на рис. 7.1 и 7.10, при T = 10 представлены на рис. 7.12 — (а) и (б), соответственно. (Стрелки, соответствующие дугам в графах, опущены в связи с их избыточностью.)

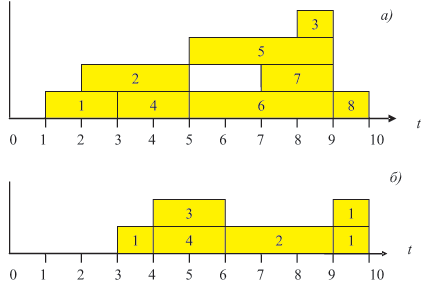
Рис. 7.12. Диаграммы выполнения работ при поздних сроках окончания: а — для графа на рис. 7.1,б — для графа на рис. 7.10

Пусть 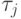$\tau _{j}$ — произвольное значение момента окончания выполнения j -й работы, j =1 , ... , m,

$\tau _{1j} \le \tau _{j} \le \tau _{2j}(T) (\tau _{j} \in [\tau _{1j}, \tau _{2j}(T)])$ .

Меняя значения 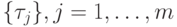$\{ \tau _{j}\} , j = 1 , \dots ,m$ , но соблюдая при этом порядок следования работ, мы получим множество допустимых расписаний выполнения работ.

Нашей конечной целью является выбор таких расписаний, которые позволяют решить задачи 1 и 2.

Дальше >>

Параллельное программирование

Параллельное программирование — аппарат исследования операций

Временные оценки на информационных графах

Вопросы и ответы

Авторизоваться

Параллельное программирование

Параллельное программирование — аппарат исследования операций

Временные оценки на информационных графах

Вопросы и ответы