Логики вполне достаточно

Эквивалентность

Для доказательства или опровержения тавтологий, противоречий, выполнимости построение таблиц истинности с их

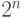
Операция эквивалентности поможет определить такие правила. Она использует символ равенства "=" и имеет таблицу истинности (и это будет последняя таблица истинности), устанавливающую, что a = b имеет значение True, если и только если a и b оба имеют значение True либо оба имеют значение False.

Операция коммутативна (a = b всегда имеет то же значение, что и b = a). Операция рефлексивна, и это означает, что a = a является тавтологией для любого a.

Хотя логики чаще используют для эквивалентности символ ⇔, символ равенства также является подходящим, поскольку равенство в обычном смысле подразумевает эквивалентность: выражение a = b имеет значение True, если и только если a и b имеют одинаковые значения. Следующее свойство расширяет это наблюдение.

Теорема: "Подстановка"

Набросок доказательства: если u не содержится в e, то e'совпадает с e, и по свойству рефлексивности e = e является тавтологией. Пусть теперь u входит в e. Заметим, что для каждого истинностного присваивания значение выражения полностью определяется значениями входящих в него подвыражений. Выражения e и e' отличаются только подвыражениями u и v, которые для данного присваивания имеют совпадающие значения, ввиду тавтологии u = v. Поскольку все подвыражения совпадают, будут и совпадать сами выражения e и e'. Данное рассуждение справедливо для любого истинностного присваивания. Отсюда следует, что на всех присваиваниях выражения e и e' имеют совпадающие значения, а следовательно, e = e' является тавтологией.

Это правило является ключом к доказательству нетривиальных булевских свойств. При доказательстве мы будем применять таблицы истинности только для базисных выражений, а затем, используя эквивалентность, заменим выражения на более простые. Например, рассмотрим выражение:

(a and (not (not b))) = (a and b)    — Цель

Для доказательства того, что это выражение является тавтологией, нет необходимости выписывать таблицу истинности. Докажем прежде, что для любого выражения x следующие общие свойства являются тавтологиями:

not (not x) = x                                  T1
x = x                                                   T2

Утверждение T2 следует из рефлексивности эквивалентности =. Доказать T1 просто. Затем можно применить T1 к выражению b и использовать теорему о подстановке, заменяя not (not b) на b в левой части выражения "Цель". После чего остается применить T2 к a and b, получив желаемый результат.

Мы будем использовать пару символов "/=" для выражения того, что два булевских значения не эквивалентны. По определению a /= b имеет то же значение, что и not (a = b).

Законы Де Моргана

Две тавтологии представляют особый интерес в использовании and, or и not.

Теоремы: "Законы Де Моргана"

Доказательство: либо напишите таблицы истинности, либо, что лучше, комбинируйте принципы исключенного третьего, непротиворечивости, дизъюнкции и конъюнкции.

Эти свойства четко проявляют двойственность, характерную для операций and-or. Отрицание одной из этих операций эквивалентно применению другой операции над отрицаниями операндов.

Неформальная интерпретация: "Если кто-то говорит, что неверно, что имеет место a or b, то это все равно, если бы он сказал, что ни a, ни b не выполняются".

Конечно, мы уже находимся на этапе, когда формальные нотации с их точностью и лаконичностью значительно превосходят предложения естественных языков.

Другой аспект тесной ассоциации между операциями or и and состоит в том, что каждая из них дистрибутивна по отношению к другой. Смысл этого отражается в следующих двух тавтологиях.

Теоремы: "Дистрибутивность булевских операций"

Сравните с дистрибутивностью умножения по отношению к сложению в математике: для любых чисел m, p, q выражение m * (p + q) эквивалентно (m * p)+ (m * q ).

Доказать дистрибутивность достаточно просто, например, через таблицы истинности. Она помогает упростить сложные булевские выражения.

Упрощение нотации

Во избежание накопления скобок для операций задаются правила приоритета, что обеспечивает стандартное понимание булевских выражений, когда опущены некоторые скобки. Идея здесь та же, что и в арифметике и языках программирования. Благодаря приоритетам мы понимаем, что в арифметическом выражении m + p * q первой будет выполняться операция умножения, имеющая более высокий приоритет. Иногда говорят, что операция умножения теснее связывает операнды, чем операция сложения.

Приоритеты булевских операций отражены в синтаксисе Eiffel. Порядок, задающий приоритеты от высшего к низшему, следующий:

• not связывает наиболее тесно;
• затем идет эквивалентность =;
• потом идет and;
• потом or;
• затем уже implies (изучаемая ниже).

По этим правилам выражение без скобок a = b or c and not d = e также законно и означает то же, что и выражение с расставленными скобками

(a = b) or (c and ((not d) = e))

Желательно все же оставлять некоторые скобки, защищая читателя от возможного непонимания, которое может привести к ошибкам.

В рекомендуемом стиле не следует опускать скобки, разделяющие or и and выражения, поскольку правила приоритета, устанавливающие, что and связывает теснее, чем or, являются спорными. Лучше сохранять скобки для not подвыражения, используемого как операнд эквивалентности, чтобы не путать (not a) = b с not (a = b). Можно опускать скобки для эквивалентности в форме x = y, где x и y являются простыми переменными. С учетом этих правил последний пример можно записать проще:

a = b or (c and (not d) = e)

Еще одно свойство, упрощающее нотацию, связано с ассоциативностью некоторых операций. В арифметике мы просто пишем m + p + q, хотя это могло бы означать m + (p + q) или (m + p)+ q, поскольку выбор порядка сложения не имеет значения. При любом порядке результат будет одинаков, потому что операция сложения обладает свойством ассоциативности. Этим же свойством в арифметике обладает операция умножения, но им не обладает операция деления. Для умножения два выражения m * (p * q) и (m * p)* q дают одинаковый результат. В булевской логике обе операции and и or являются ассоциативными, что выражается следующими тавтологиями:

(a and (b and c)) = ((a and b) and c)
(a or (b or c)) = ((a or b) or c)

Указание для доказательства: можно, конечно, построить таблицу истинности, но проще использовать предыдущие правила. Для доказательства первой тавтологии следует использовать принцип конъюнкции. Дважды применяя это принцип к левой части эквивалентности, устанавливаем, что левая часть истинна, если и только если все переменные, в нее входящие, имеют значение True. Аналогичный результат справедлив и для правой части. Следовательно, обе части эквивалентности дают одинаковые результаты на всех истинностных присваиваниях и выражение является тавтологией. Вторая тавтология доказывается аналогично с использованием принципа дизъюнкции.

Это позволяет нам писать выражения в форме a and b and c или a or b or c без риска появления недоразумений. Обобщая:

Почувствуй стиль