Логики вполне достаточно
Конъюнкция
Подобно or, операция and имеет два операнда. Если a и b являются булевскими выражениями, то булевское выражение a and b имеет значение True, если и только если a и b оба имеют это значение. Соответственно, оно имеет значение False, если и только если хотя бы один из операндов имеет это значение. Это отражено в таблице истинности.
Применение операции and к двум значениям известно как их конъюнкция, аналог конъюнкции двух событий: "Только конъюнкция (сочетание) полной луны и низкой орбиты Сатурна принесет Стрельцам истинное любовное приключение" (возможно, гороскопы не есть главное дело для логиков).
Изучение and и or показывает их близкое соответствие – двойственность. Многие свойства одной операции могут быть получены из свойства другой простым обменом True и False. Например, принцип дизъюнкции двойственно применим к конъюнкции.
Теорема: "Принцип конъюнкции"
Подобно or, операция and коммутативна: для любого a и b, a and b имеет значение такое же, как b and a. Это свойство следует из таблицы истинности, а также является следствием принципа конъюнкции.
Сложные выражения
Вы можете использовать булевские операции – три уже введены, not, or и and, а две будут описаны ниже – для построения сложных булевских выражений. Для таких выражений также можно задать таблицу истинности. Вот пример такой таблицы для выражения a and (not b):
| a | b | not b | a and (not b) |
| True | True | False | False |
| True | False | True | True |
| False | True | False | False |
| False | False | True | False |
Для порождения этой таблицы достаточно заменить в истинностной таблице для and каждое значение b значением not b, полученным из истинностной таблицы для not; третий столбец добавлен, чтобы показать not b.
Сложные выражения
Булевская переменная может принимать значение True или False. Значение булевского выражения зависит от значений его переменных. Например, при построении истинностной таблицы для выражения a and (b and (not c)) мы видим, что это выражение имеет:
- значение True если a и b имеют значение True, а c имеет значение False;
- значение False во всех остальных случаях.
Следующее понятие помогает выразить такие свойства.
Определение: Истинностное присваивание
Так что мы можем сказать, что выражение a and (b and (not c)) имеет значение True в точности для одного истинностного присваивания (True для a, True для b, и False для c) и False для всех остальных истинностных присваиваний.
Каждая строка истинностной таблицы некоторого выражения соответствует, один в один, истинностному присваиванию его переменных.
Достаточно просто заметить, что для выражения, содержащего n переменных, существует ровно
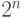
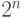
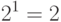


- Первые n столбцов каждой строки перечисляют значения каждой из переменных соответствующего истинностного присваивания.
- Последний столбец дает значение выражения, соответствующее этому истинностному присваиванию.
Только для целей пояснения в таблицу последнего примера добавлен столбец для not b)
Если для некоторого истинностного присваивания выражение имеет значение True, то будем говорить, что истинностное присваивание удовлетворяет выражению.
Например, уже рассмотренное присваивание – True для a, True для b, False для c – удовлетворяет a and (b and (not c)); все остальные – нет.
Тавтологии
Нас часто будут интересовать выражения, имеющие значение True для всех истинностных присваиваний. Рассмотрим
a or (not a)
Истинность этого выражения следует из того, что истинно одно из двух утверждений:
- a имеет значение True;
- not a имеет значение True.
Это неформальная интерпретация. Формально следует построить таблицу истинности.
Строго говоря, второй столбец не является частью таблицы истинности; он дает значение для not a, приходящее из таблицы истинности для not. Комбинируя эти значения с таблицей истинности для or, получаем значения третьего столбца.
Из этого столбца видим, что любое истинностное присваивание (в данном случае переменная только одна) переменной a удовлетворяет выражению. Выражения с таким свойством имеют собственное имя.
Определение: Тавтология
То, что выражение a or (not a) является тавтологией, ранее было установлено как принцип исключенного третьего.
Другими простыми тавтологиями, которые вам следует проверить, построив их таблицу истинности, являются:
Двойственными к тавтологиям являются выражения, которые никогда не принимают значения True.
Определение: Противоречие
Например, (снова проверьте таблицу истинности) a and (not a) является противоречием. В другой формулировке об этом же говорит принцип непротиворечивости.
Из этих определений и таблицы истинности для not следует, что выражение a является тавтологией, если и только если not a является противоречием. Справедливо и обратное утверждение.
Выражение, имеющее значение True хотя бы для одного истинностного присваивания, называется выполнимым. Очевидно:
Существуют, конечно же, выполнимые выражения, не являющиеся тавтологиями. Они имеют значение True по крайней мере для одного истинностного присваивания и значение False для другого хотя бы одного присваивания. Таковыми являются, например, выражения a and b и a or b.
Из того, что выражение "a не является тавтологией", вовсе не следует, что "not a является тавтологией". Выражение a не является тавтологией, но может быть выполнимым, а значит, существует такое истинностное присваивание, при котором a примет значение True, но для этого же присваивания выражение not a будет иметь значение False и, следовательно, не будет являться тавтологией.
