НОУ ИНТУИТ | Оконечные устройства и линии абонентского участка информационной сети. Лекция 10: Кодирование с адаптивным предсказанием

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 26.10.2007 | Доступ: свободный | Студентов: 2354 / 787 | Оценка: 4.04 / 3.76 | Длительность: 17:47:00

ISBN: 978-5-94774-810-9

Темы: Сетевые технологии, Аппаратное обеспечение

Специальности: Администратор коммуникационных систем, Архитектор программного обеспечения

|

Вам нравится? Нравится 23 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Краткие итоги

В настоящее время при передаче информации в сотовых сетях связи и передаче речи по Internet (IP-телефония) очень популярны методы кодирования с предсказанием.
Принцип предсказания. На передающей стороне устанавливается предсказатель, которой по полученной в предыдущий момент времени информации вырабатывает (предсказывает) последующую информацию. При поступлении информации от передатчика предсказанное и истинное значение сравниваются (вычитаются) и передается ошибка предсказания. На приемном конце устанавливается предсказатель, который по предыдущей информации вырабатывает последовательные значения сигнала (те же самые, что и предсказатель передатчика) и корректирует (суммирует) с поступившим сигналом ошибки.
Кодирование с предсказанием основывается обычно на аппроксимации формы сигнала, т.е. кодирование кривой с помощью значений этой кривой в отдельных точках и восстановление ее формы на приемном конце по этим отдельным отсчетам.
При линейной аппроксимации каждая кривая может быть представлена с произвольной точностью суммой величин предыдущих отсчетов, умноженных на коэффициенты, которые называются коэффициентами предсказания.
При дифференциальной импульснокодовой модуляции в линию передается разность между текущим и предыдущим значениями.
Выигрыш от кодирования на практике легче оценивать по мощности. Поэтому выигрыш от кодирования измеряют отношением мощности кодирования при равномерном и при разностном квантовании.
Система с разностным предсказанием становится неэффективной при большом значении разностного сигнала.
Это может произойти из-за возрастания разности соседних отсчетов или из-за нарушения системы предсказания.
Имеются методы, основанные на вероятностных методах предсказания. Они рассматривают последовательные n отсчетов как n случайных величин и определяют вероятность их совместного появления [10.8] — $p(x_{1}, …, x_{k}$ ). Прогнозирование всего отсчета основано на определении математического ожидания.
Вероятностные методы связаны с нахождением оптимального соотношения сбора отсчетов (чем больше, тем лучше) и своевременной реакцией на изменения (чем больше собранных отсчетов, тем реакция медленнее).
Работа вокодера (voice coder) основана на анализе характерных особенностей человеческой речи.
Энергия речевого сигнала распределяется во времени только в некоторых частотных диапазонах и различается по величине. Отдельные пики энергии, возникающие в одном частотном диапазоне, называются фонемами. Частоты, на которых в данный момент возникают комбинации пиков (фонем), называются "частотами формант" или просто "формантами".
По принципу определения параметров фильтровой функции различают следующие типы вокодеров: канальные (полосные, channel); формантные; ортогональные; вокодеры с линейным предсказанием.
Основная задача процесса кодирования в вокодере — определить спектр сигнала, мощности в каждом диапазоне частот за достаточно длинный отрезок времени, в который существует форманта. Полученная информация передается на приемный конец, где она используется для управления цифровым генератором.
Ортогональные вокодеры отличаются от полосовых тем, что функции фильтров выполняются с помощью цифровых методов.
Формантный вокодер определяет и передает положение пика энергии в частотном диапазоне, амплитуду спектральных пиков. Вследствие этого снижается объем передаваемой информации.
Этот тип вокодера, в отличие от предыдущих типов, для передачи речи применяет не фильтры, а систему линейного предсказания. Как уже упоминалось, в линию передается разностный сигнал между истинным и предсказанным значением. Коэффициенты предсказания используются для предсказания управления восстанавливающим генератором на приеме и добавления генератором шума для передачи глухих и "свистящих" согласных.
Многоимпульсное кодирование (MPLPC — Multi-Pulse LPC) отличается от LPC тем, что предсказание касается не основного тона, а параметров передаваемых и принимаемых импульсов, а это более похоже на методы адаптивного кодирования.
Линейное предсказание с возбуждением усеченного остаточного сигнала (RELP-Residual Excited Linear Predication) отличается тем, что в результате обработки кодируется и предсказывается нижняя часть речевого спектра, а это уменьшает число обрабатываемых и предсказываемых отсчетов.
Линейное предсказание с кодовым возбуждением (CELP — math Excited Linear Prediction) занимает промежуточное место между кодерами формы сигнала и параметрическими вокодерами. При этом методе вместо кодирования сигналов отсчет за отсчетом кодером разностного сигнала применяется "кодовая книга возбуждения".

Задачи и упражнения

Преположим:

Сигналы на выходе квантователя имеют дапазон от 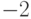до и шаг квантования 0,5

На вход в течение каждого момента времени зависит от текущего значения сигнала и задается матрицей преходных вероятностей (таблица 10.3).

Таблица 10.3. Матрица переходных вероятностей
	-2,0	-1,5	-1,0	-0,5	+0,5	+1,0	+1,5	+2,0
-2,0	0,05	0,15	0,30	0,15	0,15	0,05	0,1	0,05
-1,5	0,15	0,05	0,3	0,15	0,15	0,05	0,1	0,05
-1,0	0,1	0,3	0,15	0,2	0,15	0,05	0,1	0,05
-0,5	0,05	0,05	0,15	0,15	0,3	0,15	0,1	0,05
+0,5	0,05	0,05	0,05	0,15	0,15	0,3	0,2	0,05
+1,0	0,05	0,1	0,05	0,15	0,2	0,05	0,3	0,1
+1,5	0,05	0,1	0,05	0,1	0,1	0,25	0,05	0,3
+2,0	0,05	0,05	0,05	0,15	0,15	0,3	0,2	0,05

Определите сигналы, передаваемые в сдучае поступления последовательности показанной в табл. 10.4.

Таблица 10.4. Последовательности сигналов поступающих на вход
момент времени	Уровень сигнала
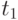$t_{1}$	-1,5
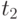$t_{2}$	-1,5
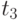$t_{3}$	-0,5
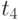$t_{4}$	+1,0
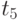$t_{5}$	+1,5
$t_{6}$	+2,0

Пример:

Пусть предыдущий сигнал был равен -2,0 .

Определите сигнал, передаваемый в линию.

Определим величину математическое ожидание поступления следующего сигнала.

-2,0     -1,5     -1,0     -0,5     +0,5     +1,0     +1,5     +2,0
-2,0    0,05     0,15     0,30     0,15     0,15      0,05     0,1     0,05

$M (x) = (-2,0) \times 0,05 + (-1,5) \times 0,15 + (-1,0) \times 0,30 + \\+(-0,5) \times 0,15 + (0,5) \times 0,15 + (1,0) \times 0,05 + (1,5) \times \\0,1 + (2,0) \times 0,05 = -0,1 - 0,225 — 0,3 — 0,075 + \\+0,075 + 0,05 + 0,15 + 0,1 = -0,0325$

Пусть поступает следующий сигнал ( —1,0) . Тогда в линию переадется сигнал равный

Y(x) — M(x)=- 0,625 .

В линию передается этот сигнал —0,625 .

Используя данные таблицы 10.5, определите значение выходного сигнала, используя формулу

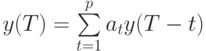
$y(T)=\sum\limits_{t=1}^{p}a_ty(T-t)$

где

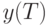y(T) — отсчет на выходе в следующий момент времени;

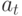$a_{t}$ — коэффициент аппроксимации;

— порядок модели.

Таблица 10.5. Перечень коэффициентов определяющих выходной сигнал
моменты времени	коэффициенты аппроксимации
моменты времени	$Y(t_{1})$	$Y(t_{2})$	$Y(t_{3})$	$Y(t_{4})$	$Y(t_{5})$	$Y(t_{6})$	$Y(t_{7})$	$Y(t_{8})$
$t_{1}$	0,3	0,3	0,4
$t_{2}$		0,2	0,2	0,6
$t_{3}$			0,15	0,1	0,75
$t_{4}$				0,2	0,5	0,3
$t_{5}$					0,5	0,2	0,3
$t_{6}$						0,3	0,3	0,4
$t_{7}$	0,15						0,15	0,7
$t_{8}$	0,2	0,2						0,6