|
Можно ли, используя функцию Дирихле, построить модель пространства, в котором нет иррациональных чисел, а есть только рациональные числа? Очевидно, нельзя построить плоскость, не используя при этом иррациональные числа, так как плоскость непрерывна. Но пространство обладает бо-льшим числом измерений и может сохранить непрерывность в каком-либо одном из них. |
Совокупности и отношения
Чтобы задать функцию, нужно указать некоторый способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции, то есть способ описания закона f. Функция может задаваться аналитическим, графическим, табличным или словесным способом.
Аналитическое выражение - формула, указывающая, какие математические действия надо произвести над аргументом x, чтобы получить соответствующие значения y. Способ задания значений функции с помощью аналитического выражения называется аналитическим способом задания функции . Функция может быть задана и с помощью нескольких различных аналитических выражений с разными областями определения. В этом случае область определения функции - область определения каждого из этих аналитических выражений (при условии, что эти отдельные области нигде "не конфликтуют"). Аналитически функция задается, если область ее определения не является конечной, особенно, в теоретических проблемах.
Пример.Рассмотрим кусочно-аналитически заданную функцию
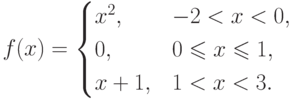
При табличном задании функции ряд дискретных значений аргумента x1, x2,..., xn и соответствующих им значений функции y1, y2,..., yn задаются в виде таблицы.
Пример.Различные статистические и социологические данные записывают в виде таблиц: уровня жизни, динамики безработицы, численности населения и т.п.
Третьим способом задания функции является графический способ.
Абсциссой x точки (x;y) на плоскости xOy называется длина отрезка [O;x], отсекаемого от точки отсчета O оси Ox плоскости. Ординатой этой точки называется длина отрезка [O;y] оси Oy плоскости xOy .
Графиком функции y=f(x) называется множество точек (x;y) на плоскости xOy (геометрическое место точек на плоскости), каждая из которых обладает тем свойством, что ее абсцисса есть значение аргумента функции, а ордината - соответствующее этому аргументу значение функции. Графически функция определяется обычно в экспериментальных науках, например, в разделах физики, химии.
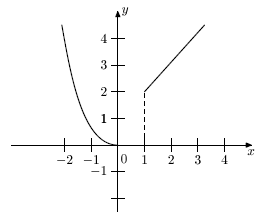
Пример.График кусочно-заданной на интервале (-2;3) функции f(x), приведенной выше, будет иметь вид, изображенный рис. 4.1. Хотя этот график и состоит из трех "вроде бы" самостоятельных частей (часть параболы; часть оси Ox ; часть прямой, параллельной биссектрисе координатного угла), тем не менее, это один график (график одной кусочно-заданной функции). График функции может не быть непрерывной линией. При x=1 указанный на рис. 4.1. график теряет свойство быть непрерывным. Функция имеет при x=1 разрыв (о разрывах функции мы подробнее поговорим ниже).
При словесном задании функции словесно указываются множества X, Y и закон f.
Пример. Функция Дирихле, рассмотренная нами выше, была определена словесно, так как значения из множеств X, Y - "словесны, расплывчаты".
Если задана некоторая однозначная функция 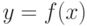 ,
,  ,
,  , то каждому значению
, то каждому значению  ставится в соответствие только одно значение
ставится в соответствие только одно значение  . Если при этом каждому значению
. Если при этом каждому значению  соответствует лишь одно значение
соответствует лишь одно значение  , то говорят, что отображение f есть взаимно однозначное отображение .
, то говорят, что отображение f есть взаимно однозначное отображение .
Так как каждому  в этом случае ставится в соответствие одно значение
в этом случае ставится в соответствие одно значение  , то можно говорить, что определена функция вида
, то можно говорить, что определена функция вида 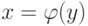 с областью определения
с областью определения  и областью значений
и областью значений  .
.
Функция 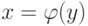 называется функцией, обратной к (прямой) функции y=f(x) . Обратную к f функцию g часто обозначают f-1 (g=f-1).
называется функцией, обратной к (прямой) функции y=f(x) . Обратную к f функцию g часто обозначают f-1 (g=f-1).
Если дана функция y=f(x) и для любого значения 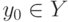 уравнение f(x)=y0 имеет единственный корень
уравнение f(x)=y0 имеет единственный корень 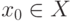 , то функция y=f(x) обратима. Если функция
, то функция y=f(x) обратима. Если функция 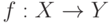 определена и возрастает (убывает) на промежутке X, то у нее существует обратная функция, причем обратная функция
определена и возрастает (убывает) на промежутке X, то у нее существует обратная функция, причем обратная функция  определена и возрастает (убывает) на Y. Таким образом, график обратной функции
определена и возрастает (убывает) на Y. Таким образом, график обратной функции 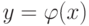 симметричен с графиком данной функции y=f(x) относительно биссектрисы первого и третьего координатных углов.
симметричен с графиком данной функции y=f(x) относительно биссектрисы первого и третьего координатных углов.
Пример.
Функция y=x2 с областью определения D(f)=R, областью изменения 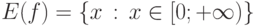 и функция
и функция  не является взаимно
однозначной, а функция y=x3 с обратной
однозначной функцией
не является взаимно
однозначной, а функция y=x3 с обратной
однозначной функцией ![x=\sqrt[3]{y}](/sites/default/files/tex_cache/792d1c3ee23e28c1e0d0e3ec30bb379f.png) - взаимно однозначная.
- взаимно однозначная.
Пусть дано некоторое соотношение, связывающее две переменные x и y. Если все его члены перенести в левую часть, то оно запишется в виде: F(x,y)=0. Если существуют различные пары действительных чисел (x,y), удовлетворяющих данному соотношению, то соотношение F(x,y)=0 можно считать способом задания переменной y как функции от x. С помощью этого соотношения каждому значению  ставится в соответствие
ставится в соответствие  (фиксируем каждый раз x, решаем, при фиксированном x, уравнение и находим y ). Функция от x, определяемая соотношением F(x,y)=0, называется неявно заданной функцией .
(фиксируем каждый раз x, решаем, при фиксированном x, уравнение и находим y ). Функция от x, определяемая соотношением F(x,y)=0, называется неявно заданной функцией .
Пример.Соотношение 2x-y+1=0 неявно задает y
как функцию от x ; эту функцию можно выразить явно,
разрешив уравнение относительно y: y=1+2x.
Соотношение x2+y2-1=0 неявно задает двухзначную
функцию 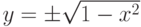 ; уравнение
; уравнение 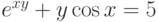 задает неявную функцию y (не выражаемую явно через x ).
задает неявную функцию y (не выражаемую явно через x ).
Функция f(x) называется четной, если f(x)=f(-x) для всех  , где X - область определения функции y=f(x) . График четной функции симметричен относительно оси Oy. Функция называется нечетной, если f(x)=-f(-x), для любого
, где X - область определения функции y=f(x) . График четной функции симметричен относительно оси Oy. Функция называется нечетной, если f(x)=-f(-x), для любого  . График нечетной функции симметричен относительно начала координат. Области определения четной и нечетной функции симметричны относительно начала координат. Функция может быть ни нечетной, ни четной.
. График нечетной функции симметричен относительно начала координат. Области определения четной и нечетной функции симметричны относительно начала координат. Функция может быть ни нечетной, ни четной.
Пример. Функция y=x2cos(x) - четная, так как y(-x)=(-x)2cos(-x)= x2cos(x)=y(x), а функция y=x2sin(x) - нечетная, так как y(-x)=(-x)2sin(-x)=-x2sin(x)=-y(x). Функция y=x+2 не является ни четной, ни нечетной, так как y(-x)=-x+2.