НОУ ИНТУИТ | Введение в математику. Лекция 4: Совокупности и отношения

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Кабардино-Балкарский государственный университет

Опубликован: 18.04.2007 | Доступ: свободный | Студентов: 12044 / 2526 | Оценка: 4.16 / 4.04 | Длительность: 14:52:00

ISBN: 978-5-9556-0105-2

Тема: Математика

Специальности: Математик

|

Вам нравится? Нравится 124 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Функция называется периодической с периодом T 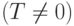$(T\ne 0)$ , если для всех $x\in X$ выполнено: f(x)=f(x+T) , то есть значения функции повторяются через каждый промежуток длины . График такой функции получается повторением части графика, определенного на интервале 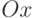длины .

Пример.Функция y=sin(x) является периодической с периодом 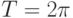$T=2\pi$ .

Функция y=f(x) называется монотонно возрастающей на некотором участке области определения функции, если для всех 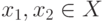$x_1,x_2\in X$ , таких, что x₁<x₂, имеет место неравенство f(x₁) < f(x₂) .

Функция y=f(x) называется монотонно убывающей на некотором участке области определения функции, если для всех 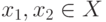$x_1, x_2\in X$ , таких, что x₁<x₂, имеет место неравенство f(x₁)> f(x₂) .

Пример. Функция y=x² монотонно убывает на промежутке $({-\infty};0)$ и монотонно возрастает на промежутке $(0;{+\infty})$ . Действительно, из 0<x₁<x₂ следует, что f(x₁)<f(x₂), а из x_1<x_2<0 следует, что f(x₁)>f(x₂), f(x₂)=x₂², f(x₁)= x_1^2 .

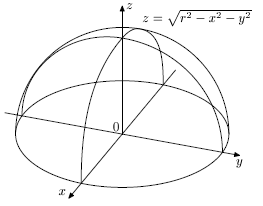
График функции y=f(x) - некоторая линия в плоскости xOy. Выясним, что является графиком функции нескольких переменных, для наглядности ограничиваясь двумя переменными, то есть функцией z=f(x₁,x₂)=f(x,y). Область D(f) - множество точек на плоскости xOy. Каждой точке M(x₀;y₀) на плоскости соответствует число z₀=f(x₀;y₀), то есть тройка связанных функцией z=f(x,y) чисел (x₀;y₀;z₀) определяет точку N₀(x₀;y₀;z₀). Совокупность всех точек N(x;y;z)=N(x;y;f(x,y)), $(x,y)\in D(f)$ образует некоторую поверхность в пространстве xyz - график функции z=f(x,y) (геометрическое место точек N, рис. 4.2.).

Рис. 4.2. График функции двух переменных

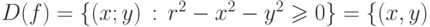Пример. Дана функция $z=\sqrt{r^2-x^2-y^2}$ . Область определения $D(f)=\{(x;y)\,:\, r^2-x^2-y^2\ge 0\} = \{(x,y)$ : $x^2+y^2\le r^2\}$ - круг радиуса r с центром O(0;0). График функции - верхняя половина сферы с радиусом r (рис. 4.3). Связь координат произвольной точки на этой полусфере:

$x^2+y^2+z^2= r^2 \ \implies \ r^2-x^2-y^2=z^2 \ \implies \\ \implies \begin{cases} z=\sqrt{r^2-x^2-y^2} \ &\text{--- верх сферы}, \\ z=-\sqrt{r^2-x^2-y^2}\ &\text{--- низ сферы}. \end{cases}$

Рис. 4.3. Верхняя полусфера

С графиками функций можно выполнять следующие операции и процедуры: сложение, вычитание, сдвиги относительно осей координат, сжатие и растяжение и др.

Многие науки часто имеют дело со сравнениями множеств, с выяснением связей элементов множеств. Для формализации таких процессов используется понятие "отношение".

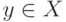Отношение r, определенное над элементами множества X, - это некоторое правило, по которому каждый элемент $x\in X$ связывается с другим (другими) элементом (элементами) $y\in X$ . Отношение r называется n - арным отношением, если оно связывает n различных элементов X . При n=1 - отношение называется унарным , при n=2 - бинарным , при n=3 - тернарным .Множество пар (x,y), которые находятся в бинарном ( 2 -арном) отношении друг к другу, - подмножество декартового множества $X\times Y$ . Отношение r элементов $x\in X$ , $y\in Y$ обозначают как $x \to\limits^{r} y$ , r(x,y) или r(X,Y).

Пример.Рассмотрим классическую схему ЭВМ из устройств: 1 - ввода, 2 - логикоарифметическое, 3 - управления, 4 - запоминающее, 5 - вывода. Отношение "информационный обмен" определим так: устройство i находится в отношении r с устройством j, если из устройства i в устройство j поступает информация. Тогда можно это отношение задать матрицей R отношений (наличие r на пересечении строки i и столбца j матрицы означает, что устройство i находится в этом отношении с устройством j, а наличие $\emptyset$ - что отношение отсутствует):

$R= \begin{Vmatrix} \emptyset & r & r & r & \emptyset \cr \emptyset & \emptyset & r & r & r \cr r & r & \emptyset & r & r \cr \emptyset & r & r & \emptyset & r \cr \emptyset & \emptyset & r & \emptyset & \emptyset \end{Vmatrix}$

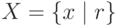Отношение, задаваемое фразой "для каждого x из множества X ", обозначается $\forall x\in X$ и называется квантором общности , а отношение "существует такое x из множества X " - имеет обозначение $\exists x\in X$ и называется квантором существования . Факт, что элементы $x\in X$ связаны, выделены некоторым отношением r, обозначают как X={x:r} или записывают в виде $X=\{x\mid r\}$ .

Композиция ( произведение ) $r=r_1\circ r_2$ отношений r₁ и r₂ заданных над одним и тем же множеством X - это третье отношение r, определяемое так:

$x \to\limits^{r} y \ \iff \ \Bigl (\exists z\in X\,:\, (x \to\limits^{r} z), \ (z \to\limits^{r} y) \Bigr).$

Отношение r называется отношением тождества, если выполнено условие

$x \to\limits^{r} y \ \iff \ (x=y).$

Отношение r называется рефлексивным, если выполнено условие

$((\forall x\in X)\,:\, x \to\limits^{r} x).$

Отношение r называется транзитивным, если выполнено условие

$((x \to\limits^{r} y), \ (y \to\limits^{r} z)) \ \implies \ (x \to\limits^{r} z).$

Отношение r называется симметричным, если выполнено условие

$(x \to\limits^{r} y ) \ \implies \ (y \to\limits^{r} x).$

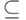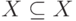Пример. Бинарное отношение, определяемое знаком " = " - рефлексивно, транзитивно. Бинарное отношение "иметь общий делитель" - симметрично. Бинарное отношение " $\subseteq$ " вложенности множеств - рефлексивно, антисимметрично, транзитивно. Отношение параллельности двух прямых - транзитивно, рефлексивно, симметрично. Проверим предпоследнее утверждение. Рефлексивность следует из соотношения $X\subseteq X$ (для любого множества). Симметричность не выполняется, так как из условия 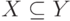$X\subseteq Y$ не следует 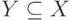$Y\subseteq X$ для любых X, Y. 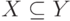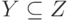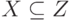Транзитивность следует из того, что из условий $X\subseteq Y$ , $Y\subseteq Z$ следует и условие $X\subseteq Z$ .

Частично упорядоченным по отношению r множеством X называется множество, на котором задано отношение r(X), являющееся транзитивным, несимметричным, рефлексивным. Упорядоченное по отношению r(X) множество - это множество X, такое, что $\forall x,y\in X$ , либо $x \to\limits^{r} y$ , либо $y \to\limits^{r} x$ . Для частично упорядоченного множества отношение определено не для всех (связываемых этим отношением) элементов множества.

Отношение частичного упорядочивания называется просто порядком , а отношение упорядочивания - полным порядком .

Пример. Отношение r(x,y): " x кратно y " (или $\mod (x,y)=0$ ), определенное на множестве натуральных чисел N, как легко проверить, является отношением частичного порядка. Отношение r(x,y): " $x\le y$ " определенное на множестве вещественных чисел R, - отношение частичного порядка и полного порядка. Отношение r(x,y): " x<y " определенное на R, не является отношением полного порядка (не рефлексивно). Отношение вложенности множеств (см. выше) " $x\subseteq y$ " - отношение частичного упорядочивания множеств, определенное на множестве всех множеств, но оно не является отношением полного порядка (не для любых двух множеств имеет место включение в ту или иную сторону; множества могут быть и различной природы).

Транзитивное, рефлексивное, симметричное отношение r(X) называется отношением эквивалентности . Такие отношения очень важны и нужны, так как они разбивают множество X на классы, классы эквивалентности - непустые и непересекающиеся подмножества, каждое из которых вместе с любым своим элементом содержит также все элементы X, эквивалентные ему по отношению r(X), и не содержит других $x\in X$ .

Пример.В различных исследованиях часто используется группировка и классификация заданных объектов по некоторым признакам, например, при исследовании уровня социальной защищенности необходимо рассматривать различные социальные группы. При решении таких задач используют те или иные отношения классификации, группировки, отношения эквивалентности. Например, отношение "средний годовой доход социальной группы" позволяет группировать население для опроса и социологических исследований.

Соответствие S - это бинарное отношение r над множеством $X\times Y$ :

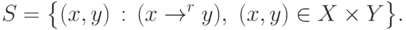
$S= \bigl\{(x,y) \,:\, (x \to\limits^{r} y), \ (x,y)\in X\times Y\bigr\}.$

Обратное соответствие к r - это соответствие $S^{-1}\subseteq Y\times X$ вида:

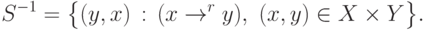
$S^{-1}= \bigl\{(y,x) \,:\, (x \to\limits^{r} y), \ (x,y)\in X\times Y\bigr\}.$

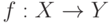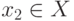Изоморфизм двух упорядоченных (по отношению r ) множеств X и Y - такое взаимно-однозначное соответствие $f:X\to Y$ , что из того, что $x_1\in X$ и $x_2\in X$ находятся в отношении r, следует, что y₁=f(x₁) и y₂=f(x₂) находятся в отношении r, и наоборот.

Дальше >>

Авторизоваться

Введение в математику

Совокупности и отношения

Вопросы и ответы