Введение в машинное обучение

1.1.6. Градиентный бустинг деревьев решений

Градиентный бустинг деревьев решений (Gradient Boosting Trees – GBT) [6, 7] – другой универсальный алгоритм машинного обучения, основанный на использовании ансамбля деревьев решений. В отличие от случайного леса градиентный бустинг является развитием бустинг-идеи. Алгоритм минимизирует эмпирический риск жадным пошаговым алгоритмом, аналогичным методу градиентного спуска. Рассмотрим, например, задачу восстановления регрессии используют. Рассмотрим суммарный штраф на обучающей выборке как функцию от значений решающего правила f в точках :

Тогда градиент функции L(f) равен

На предварительном этапе алгоритм строит оптимальную константную модель . На m-й итерации конструируется дерево решений (небольшой глубины), аппроксимирующее компоненты вектора антиградиента, вычисленного для текущей модели f. После этого значения в узлах построенного дерева перевычисляются, так, чтобы минимизировать суммарную величину штрафа Далее осуществляем присваивание , что и завершает m-ю итерацию. Здесь v – параметр регуляризации (shrinkage), призванный бороться с возможным переобучением. Он выбирается из интервала (0,1].

Для решения задачи восстановления регрессии часто используются следующие штрафные функции:

квадратичный штраф

абсолютный штраф

или функция Хьюбера

Заметим, что функция Хьюбера и квадратичный штраф дифференцируемы всюду, тогда как абсолютный штраф – везде, кроме точек, в которых .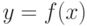

Для задачи классификации с K классами метод остается прежним, только вместо одной функции f конструируют сразу K функций 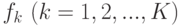. В качестве штрафа можно использовать кросс-энтропию

где

– есть оценка вероятности того, что . Итоговый классификатор определяется как

Более подробное описание алгоритма см. в [6, 7].

Другим популярным методом, использующим идею бустинга, является алгоритм AdaBoost и его модификации [5].

1.2. Кластеризация

В задачах обучения без учителя (unsupervised learning) у объектов не известны выходы, и требуется найти некоторые закономерности в данных. К задачам обучения без учителя относят задачи кластеризации, понижения размерности, визуализации и др. Здесь рассматривается только кластеризация.

Задача кластеризации – это задача разбиения заданного набора объектов на кластеры, т. е. группы близких по своему признаковому описанию объектов. "Похожие" друг на друга объекты должны входить в один кластер, "не похожие" объекты должны попасть в разные кластеры.

Близость ("похожесть") объектов измеряется на основе функции расстояния

1.2.1. Метод центров тяжести

Рассмотрим один из алгоритмов, решающих задачу кластеризации – метод центров тяжестей ( -means). На вход алгоритма поступает набор данных

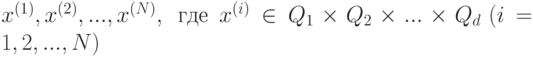
и натуральное число K – количество кластеров, на которые нужно разбить данные. Алгоритм реализует пошаговую процедуру минимизации

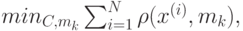
где 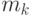– центр тяжести объектов, относящихся к k-му кластеру:

При этом не гарантируется нахождение глобального минимума. На предварительном этапе строится некоторое разбиение входных данных на K групп (например, случайно). Пусть – номер группы, к которой принадлежит -й объект. В ходе работы алгоритма значения обновляются. В конце работы алгоритма значения будут соответствовать разбиению данных на кластеры. Каждая итерация представляет собой последовательность следующих шагов:

• Вычисляем центр тяжести объектов в каждой группе.
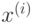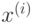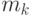• Для каждого объекта находим k, для которого расстояние от до т. е. минимально. Обновляем функцию положив .

Итерации завершаются, когда наступает стабилизация значений , либо по достижении максимального значения числа итераций.

1.2.2. Метод медиан

Метод центров тяжестей работает с явными описаниями объектов 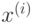Модификацией этого метода является метод медиан, или метод срединных точек, ( K–medians, или K–medoids). На вход этого алгоритма подается число кластеров K и матрица расстояний , где 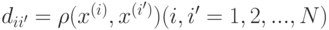. Заметим, что сама функция может быть не известна.

Алгоритм ничем не отличается от предыдущего, но вместо центра тяжестей, для каждой группы будем находить медиану, или срединную точку, , где

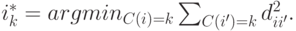
Каждая итерация представляет собой последовательность следующих шагов:

• Вычисляем медиану объектов в каждой группе.
• Для каждого объекта 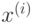находим для которого минимально. Обновляем функцию положив .

Как правило, результаты работы алгоритмов центров тяжестей и медиан (если они оба применимы к данным) близки.