Введение в машинное обучение

1.1.4. Деревья решений

Деревья решений [3] являются одним из наиболее наглядных и универсальных алгоритмов обучения. К достоинствам деревьев решений следует отнести:

• Возможность производить обучение на исходных данных без их дополнительной предобработки (нормализация и т. п.);
• Нечувствительность к монотонным преобразованиям данных;
• Устойчивость к выбросам;
• Возможность обрабатывать данные с пропущенными значения;
• Поддержка работы с входными переменными разных (смешанных) типов;
• Возможность интерпретации построенного дерева решений.

Кроме того, существуют эффективные алгоритмы их настройки (обучения), например, CART – Classification and Regression Trees [3] или See5/C5.0.

Основная идея деревьев решений состоит в рекурсивном разбиении пространства признаков с помощью разбиений (splits): гиперплоскостей, параллельных координатным гиперплоскостям (если признак – количественный), либо по категориям (если признак номинальный). В каждом из полученных в конце процедуры "ящиков" функция аппроксимируется константой:

• Для задачи классификации:
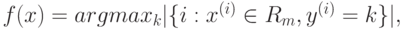
• Для задачи восстановления регрессии:

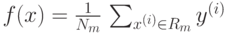
В алгоритме CART разбиения имеют вид:

• , если j-й признак количественный;
• , если j-й признак качественный, , где 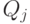– набор значений, которые может принимать j-й признак.

Дерево строится рекурсивно с помощью следующей жадной процедуры, на каждом шаге максимально уменьшая значение функции, описывающей неоднородность данных, содержащихся в узле дерева. Пусть на текущем шаге имеется разбиение пространства признаков на области (ящики) .

• Выбираем область .
• Выбираем j и c (или ), так, чтобы добиться максимального уменьшения неоднородности, или загрязненности, (impurity) .
• Строим разбиение и повторяем действия.

Разбиения проводятся до тех пор, пока в строящиеся вершины попадает достаточное количество точек обучающей выборки, или пока дерево не достигнет заданной глубины.

Используют различные способы измерить неоднородность, например,

• Для задачи классификации:
• Для задачи восстановления регрессии:

где – количество точек из обучающей выборки, попавших в область .

Другой важный параметр модели – это глубина дерева решений, регулирующая, "как сильно" будет разбито пространство признаков. Небольшое число разбиений может привести к тому, что построенная модель не будет учитывать некоторые особенности распределения признаков, описывающих те или иные классы, и таким образом приведет к уменьшению точности предсказания. Чрезмерное число разбиений может привести к переобучению модели и снижению еe обобщающей способности.

Для того чтобы избежать переобучения, используется процедура отсечений (prunning) [3].

1.1.5. Случайный лес

Один из общих подходов в машинном обучении заключается в использовании композиции "слабых" решающих правил. Итоговое правило строится путем взвешенного голосования ансамбля базовых правил. Для построения базовых правил и вычисления весов в последнее время часто используются две идеи:

• Баггинг (bagging – bootstrap aggregation): обучение базовых правил происходит на различных случайных подвыборках данных или/и на различных случайных частях признакового описания; при этом базовые правила строятся независимо друг от друга.
• Бустинг (boosting): каждое следующее базовое правило строится с использованием информации об ошибках предыдущих правил, а именно, веса объектов обучающей выборки подстраиваются таким образом, чтобы новое правило точнее работало на тех объектах, на которых предыдущие правила чаще ошибались.

Эксперименты показывают, что, как правило, бустинг работает на больших обучающих выборках, тогда как баггинг – на малых.

Одной из реализаций идеи баггинга является случайный лес [2].

Случайный лес, а точнее – случайные леса (random forests), является одним из наиболее универсальных и эффективных алгоритмов обучения с учителем, применимым как для задач классификации, так и для задач восстановления регрессии. Идея метода [2] заключается в использовании ансамбля из M деревьев решений (например, M=500), которые обучаются независимо друг от друга. Итоговое решающее правило заключается в голосовании всех деревьев, входящих в состав ансамбля.

Для построения каждого дерева решений используется следующая процедура:

• Генерация случайной подвыборки из обучающей выборки путем процедуры изъятия с возвращением (так называемая бутстрэп-выборка). Размер данной подвыборки обычно составляет 50–70% от размера всей обучающей выборки.
• Построение дерева решений по данной подвыборке, причем в каждом новом узле дерева переменная для разбиения выбирается не из всех признаков, а из случайно выбранного их подмножества небольшой мощности . Дерево строится до тех пор, пока не будет достигнут минимальный размер листа (количество объектов, попавших в него). Рекомендуемые значения: для задачи классификации p=d/3 , sz=1 для задачи восстановления регрессии , sz=3.

Одной из модификаций метода случайных деревьев является алгоритм крайне случайных деревьев (extremely random forests), в котором на каждом этапе для выбора признака, по которому будет проводиться разбиение, используется вновь сгенерированная случайная бутстрэп-выборка.

Среди достоинств алгоритма случайных деревьев можно выделить высокое качество предсказания, способность эффективно обрабатывать данные с большим числом классов и признаков, внутреннюю оценку обобщающей способности модели. Легко построить параллельную высоко масштабируемую версию алгоритма. Кроме того, доказано, что данный алгоритм не переобучается (с ростом M). Также метод обладает всеми преимуществами деревьев решений, в том числе отсутствием необходимости предобработки входных данных, обработкой как вещественных, так и категориальных признаков, поддержкой работы с отсутствующими значениями.