|
Здравствуйие! Я хочу пройти курс Введение в принципы функционирования и применения современных мультиядерных архитектур (на примере Intel Xeon Phi), в презентации самостоятельной работы №1 указаны логин и пароль для доступ на кластер и выполнения самостоятельных работ, но войти по такой паре логин-пароль не получается. Как предполагается выполнение самосоятельных работ в этом курсе? |
Самостоятельная работа 3: Оптимизация вычислений в задаче о разложении чисел на простые сомножители. Векторизация и балансировка нагрузки
Оптимизация вычислительной функции
В предыдущих разделах лабораторной работы был рассмотрен наивный подход к переносу вычислений с центрального процессора на сопроцессор. Попробуем оценить полученный результат. Для этого сравним время работы параллельной версии алгоритма на центральном процессоре и сопроцессоре Intel Xeon Phi. Для этого временно закомментируем директивы отправки вычислений на сопроцессор и скомпилируем код.
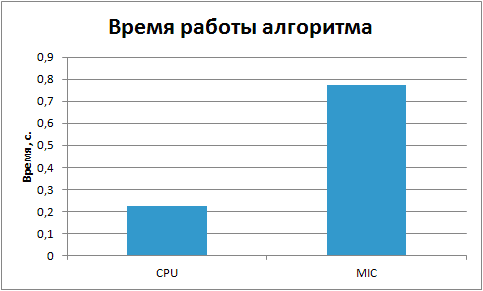
Ниже представлен график сравнения времени вычислений параллельных реализаций алгоритма факторизации чисел на процессоре и на сопроцессоре, при размере порции в динамическом планировании равным 30.
Исходя из графика видно, что лучшее время параллельного алгоритма на сопроцессоре в почти четыре раза хуже, чем время на центральном процессоре. Вместе с тем, исходя из характеристик, сопроцессор Intel Xeon Phi обладает большей пиковой производительностью.
В нашей программе все вычисления независимы. Почему не удается достичь большей производительности?
Ответ на данный вопрос следующий. Для достижения пиковой производительности ускорителя необходимо задействовать не только все ядра процессора, но и код должен быть векторизуем. Векторные операции вносят существенный вклад в пиковой производительности сопроцессора Intel Xeon Phi.
Для того чтобы понять, векторизовался ли код, необходимо собрать отчет о векторизации.
icpc -O2 -openmp -vec-report3 parMIC.cpp
Посмотрим полученный отчет:
… parMIC.cpp(174): (col. 5) remark: *MIC* loop was not vectorized: unsupported loop structure parMIC.cpp(169): (col. 3) remark: *MIC* loop was not vectorized: nonstandard loop is not a vectorization candidate …
Строки 169 и 174 соответствуют циклам функции факторизации. Циклы не векторизовались.
Intel Xeon Phi содержит регистры длиной 512 бит для векторных операций. В разрабатываемой программе используются целые числа типа int. Размер int 4 байта. Как следствие если бы код векторизовался, за раз можно было бы выполнить 16 операций.
Рассмотрим внимательно вычислительный цикл. В цикле все операции строго последовательные. Без внесения не тривиальных алгоритмических изменений его не векторизовать.
В рассматриваемой задаче основной операцией является поиск остатка от деления и сравнение с 0. Фактор имеет несравнимо малое число делителей по сравнению с количеством делений. Как правило, число не делится. Данных факт можно попробовать использовать для ускорения вычислений. Можно завести массив из 16 чисел (размер регистра). В каждый элемент массива можно вычислить остаток от деления от текущего делителя плюс индекс элемента массива. Полученные делители можно перемножить. Если результат умножения не равен нулю, то 16 чисел можно уже не проверять на делимость. В противном случае необходимо выполнить исходную проверку на делимость и сместить "окно" проверяемых делителей.
Циклы нахождения остатка и произведения векторизуемы. Ниже представлена программная реализация модификации алгоритма.
#define LOOP_SIZE 16
…
void factorization(int chunk)
{
#pragma omp parallel for schedule(dynamic, chunk)
for (int i = 1; i < NUM_NUMBERS; i++)
{
int rr[LOOP_SIZE];
int r, p;
int number = i;
int idx = number;
for (int j = 2; j < idx; j++)
{
if (number == 1) break;
#pragma simd
for(int k = 0; k < LOOP_SIZE; k++)
{
rr[k] = number % (j + k);
}
p = 1;
#pragma simd
for(int k = 0; k < LOOP_SIZE; k++)
{
p *= rr[k];
}
if(p != 0)
{
j += LOOP_SIZE - 1;
} else
{
r = number % j;
if (r == 0)
{
number /= j;
divisors[idx].push_back(j);
j--;
}
}
}
}
}
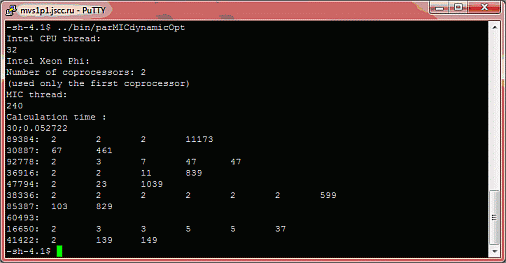
Откомпилируем и запустим код:
Ниже представлен график сравнения времени вычислений на сопроцессоре Intel Xeon Phi оптимизированной и не оптимизированной версий кода.
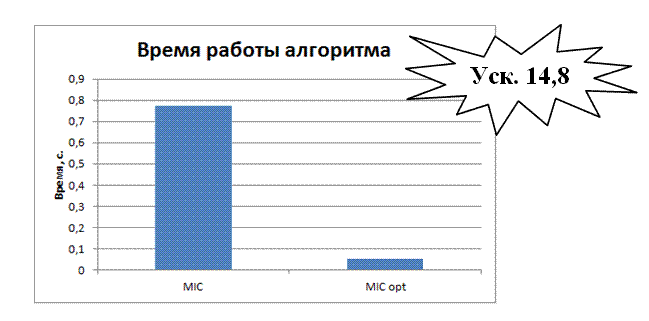
Рис. 8.18. Сравнение оптимизированной и не оптимизированной программной реализации на Intel Xeon Phi
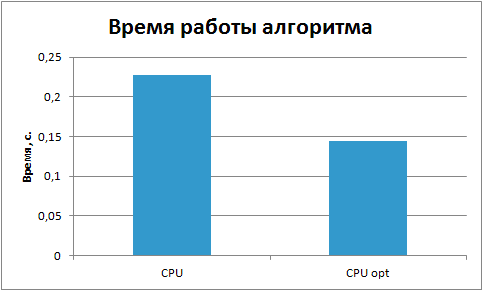
Особенностью оптимизации под Inte l Xeon Phi является то, что оптимизация также положительно влияет и на время вычислений на центральном процессоре. Ниже представлен график сравнения времени вычислений на центральном процессоре.
Из графика видно, что за счет векторизации кода, на центральном процессоре время уменьшилось в полтора раза.
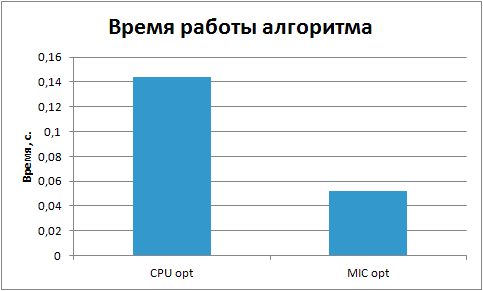
Ниже приведен график сравнение времени работы оптимизированных версий факторизации на CPU и сопроцессоры.
Из экспериментов видно, что оптимизированная реализация алгоритма факторизации на Intel Xeon Phi смогла превзойти оптимизированную версию на CPU почти в три раза.