Параллельные алгоритмы

Циклы

Под циклом будем понимать цикл типа while, рассматривая цикл типа for как частный случай. Будем также полагать, что с каждым циклом связана предшествующая ему некоторая инициализирующая часть Init, содержащая группу операторов. Инициализация необходима для обеспечения корректной работы цикла, после ее завершения должно выполняться предусловие цикла и стать истинным инвариант цикла.

С каждым циклом связывается одна или несколько переменных, называемых параметрами цикла, изменяющих свое значение при каждом выполнении тела цикла. В цикле for изменение параметров цикла осуществляется в заголовке цикла. В цикле while изменение параметров цикла выполняется явно в теле цикла.

Для простоты будем полагать, что тело цикла может содержать только операторы присваивания, условные операторы, составные операторы и операторы цикла. Мы полагаем, что цикл не содержит операторов вызова процедур и вызова функций с побочным эффектом.

Обозначим через V - множество переменных цикла. Сюда входят все переменные, встречающиеся в теле цикла, и параметры цикла, заданные в заголовке цикла for. Множество V представим как два непересекающихся подмножества:

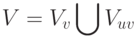
В множество 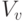входят переменные, которые могут изменять свое значение в ходе выполнения тела цикла. В это множество входят, например, параметры цикла. В множество 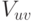входят переменные, которые сохраняют постоянное значение на всех итерациях в ходе выполнения цикла.

Аналогично обозначим через E - множество выражений, встречающихся в цикле. Множество E представим как два непересекающихся подмножества:

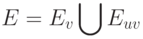
В множество 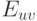входят выражения, которые содержат только константы и переменные из 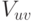. Независимо от итерации, на которой вычисляется значение этих выражений, результат вычислений будет один и тот же.

Время выполнения каждой программы определяется двумя используемыми в ней механизмами - циклами и рекурсией. Программа без циклов и рекурсивных вызовов на современных компьютерах будет выполняться практически мгновенно. Тема рекурсии останется вне нашего рассмотрения, нас будут интересовать программы с циклами.

Если программа работает недопустимо медленно, то возникает вопрос, как ускорить ее выполнение? Основным приемом является выбор эффективного алгоритма, дающего решение исходной задачи. Классическим примером может служить задача сортировки массивов. Если необходимо сортировать большое число массивов с малым числом элементов, то вполне допустимы простые методы сортировки со сложностью 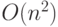. Когда n велико, такие методы становятся неэффективными, и следует применять методы со сложностью 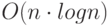. Если элементы сортируемого массива принадлежат небольшому числу классов (двум - четырем классам), то следует применять методы, имеющие сложность O(n). Примером может служить массив персон, который нужно отсортировать по полу, разделив мужчин и женщин. Другим примером является сортировка новых учеников школы Хогвартс из романа о Гарри Поттере, где сортирующая шляпа делила учеников в зависимости от их свойств на четыре класса. Такую сортировку можно выполнить за линейное время.

Выбор наилучшего алгоритма определяется не только задачей, но и архитектурой компьютера, на котором эта задача будет решаться. Алгоритм должен наилучшим образом использовать ресурсы компьютера. Алгоритм, наилучший для компьютера с одним процессором, может быть далеко не лучшим на компьютере с множеством процессоров, поскольку не будет использовать возможности распараллеливания вычислений. Распараллеливание вычислений во многом определяется возможностью распараллеливания циклов, что и будет основной темой рассмотрения в данной главе. Но прежде давайте рассмотрим более простую тему, также связанную с циклами, и имеющую ту же цель - ускорить выполнение циклов нашей программы.

Чистка цикла

Под чисткой цикла понимается избавление тела цикла от тех вычислений, которые можно выполнить один раз в инициализирующей части цикла, сохраняя эквивалентность результата выполнения цикла. Чистку цикла сведем к чистке выражений и чистке операторов цикла

Рассмотрим вначале чистку выражений. Пусть expr - некоторое выражение из Е, встречающееся в теле цикла, и subexpr - некоторое его подвыражение. Если подвыражение subexpr принадлежит множеству 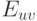, то выражение expr можно упростить. Для этого достаточно определить в Init локальную переменную loc, тип которой совпадает с типом subexpr, задать оператор присваивания loc = subexpr, затем заменить в выражении expr подвыражение subexpr переменной loc. Эту замену можно осуществить во всех вхождениях subexpr, встречающихся в выражениях из Е. Предполагается, конечно, что такая замена корректна, - subexpr не содержит вызовов функций с побочным эффектом и вхождение в expr таково, что замена subexpr на (loc) не меняет значения выражения expr.

Заметьте, что замена подвыражений локальными переменными является весьма полезным приемом, даже в тех случаях, когда вычисление подвыражения невозможно вынести из цикла. Упрощение выражений облегчает отладку, повышает надежность программы, а при наличии нескольких вхождений позволяет ускорить вычисление выражения.

Рассмотрим теперь чистку операторов. Оператор stat может быть вынесен из тела цикла и включен в конец инициализирующей части Init при условии, что все переменные этого оператора принадлежат множеству 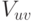и все выражения принадлежат множеству 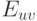. Заметьте, наше определение множества 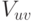не исключает включения в него переменных, входящих в левые части операторов присваивания и, следовательно, получающих значения в теле цикла. Но на такие переменные накладываются дополнительные условия. Во-первых, получаемые ими значения должны быть результатом вычисления выражений из множества 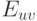. Во-вторых, эти переменные используются в выражениях только после получения ими значений в результате присваивания.

Хороший оптимизирующий компилятор может выполнять чистку цикла. Мой анализ показал, что этого нельзя сказать как о компиляторе C#, включенном в состав Visual Studio 2010, так и о JIT компиляторе, входящем в состав Framework .Net 4.0.

Вот простой пример, демонстрирующий отсутствие автоматической чистки цикла компиляторами в C# программах:

static void Main(string[] args)
        {
            double a1 = 0.5, a2 = 0.1, a3 = -1.5;
            double x = 2.0, y = 0;
            int n  = 100000;
            DateTime start, finish;
            start = DateTime.Now;
            for (int i = 0; i < n; i++)
            {
                y = (1 + 2*(a1* Math.Pow(x, 3) +
                        a2 * Math.Pow(x, 2) + a3 * Math.Pow(x, 3)) - 
                    5 * (a1* Math.Pow(x, 3) +
                        a2 * Math.Pow(x, 2) + a3 * Math.Pow(x, 3)) +
                    3 * (a1* Math.Pow(x, 3) +
                        a2 * Math.Pow(x, 2) + a3 * Math.Pow(x, 3))) /
                    (Math.Sin(a1* Math.Pow(x, 3) + 
                        a2 * Math.Pow(x, 2) + a3 * Math.Pow(x, 3)) *
                    Math.Sin(a1* Math.Pow(x, 3) +
                        a2 * Math.Pow(x, 2) + a3 * Math.Pow(x, 3)) + 
                    Math.Cos(a1* Math.Pow(x, 3) +
                        a2 * Math.Pow(x, 2) + a3 * Math.Pow(x, 3)) *
                    Math.Cos(a1* Math.Pow(x, 3) +
                        a2 * Math.Pow(x, 2) + a3 * Math.Pow(x, 3)));
            }
            finish = DateTime.Now;
            Console.WriteLine(" y = " + y);
            Console.WriteLine("Время вычислений в тиках = " +
                (finish.Ticks - start.Ticks));
        }

Нетрудно видеть, что для рассматриваемого цикла все переменные, кроме параметра цикла, принадлежат множеству 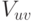, а все выражения принадлежат множеству 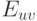. В цикле многократно встречается подвыражение, принадлежащее 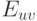, так что его вычисление можно вынести из тела цикла. Более того, сам оператор присваивания можно также вынести из тела цикла в инициализирующую часть, после чего тело цикла не будет содержать операторов, так что хороший оптимизирующий компилятор может удалить оператор цикла. Продолжая оптимизацию, можно заметить, что оператор присваивания можно заменить эквивалентным оператором

y = 1;

Однако ничего подобного не происходит. Если проанализировать IL код, построенный компилятором C# для версии Release с включенным флажком оптимизации кода, то можно видеть, что построенный код содержит несколько сотен ячеек и многократно выполняет одни и те же действия. Вот некоторый фрагмент этого кода:

IL_014c:  ldloc.0
  IL_014d:  ldloc.3
  IL_014e:  ldc.r8     3.
  IL_0157:  call       float64 [mscorlib]System.Math::Pow(float64,
                                                          float64)
  IL_015c:  mul
  IL_015d:  ldloc.1
  IL_015e:  ldloc.3
  IL_015f:  ldc.r8     2.
  IL_0168:  call       float64 [mscorlib]System.Math::Pow(float64,
                                                          float64)
  IL_016d:  mul
  IL_016e:  add
  IL_016f:  ldloc.2
  IL_0170:  ldloc.3
  IL_0171:  ldc.r8     3.
  IL_017a:  call       float64 [mscorlib]System.Math::Pow(float64,
                                                          float64)
  IL_017f:  mul
  IL_0180:  add
  IL_0181:  call       float64 [mscorlib]System.Math::Sin(float64)
  IL_0186:  mul
  IL_0187:  ldloc.0
  IL_0188:  ldloc.3
  IL_0189:  ldc.r8     3.
  IL_0192:  call       float64 [mscorlib]System.Math::Pow(float64,
                                                          float64)
  IL_0197:  mul
  IL_0198:  ldloc.1
  IL_0199:  ldloc.3
  IL_019a:  ldc.r8     2.
  IL_01a3:  call       float64 [mscorlib]System.Math::Pow(float64,
                                                          float64)
  IL_01a8:  mul
  IL_01a9:  add
  IL_01aa:  ldloc.2
  IL_01ab:  ldloc.3
  IL_01ac:  ldc.r8     3.
  IL_01b5:  call       float64 [mscorlib]System.Math::Pow(float64,
                                                          float64)

К сожалению, оптимизацию этого кода не выполняет и JIT компилятор, работающий на заключительном этапе. Приведу время, затраченное на выполнение программы:

Как видите, эта простая программа, которая в результате правильной оптимизации сводится к присвоению переменной некоторой константы и должна выполняться мгновенно, занимает неоправданно много ресурсов компьютера, как памяти, так и времени работы процессора. К сожалению, приходится еще раз констатировать, подобную оптимизацию должен выполнять сам программист, поскольку существующий компилятор с ней не справляется.

Распараллеливание цикла

Цикл допускает распараллеливание, если множество процессоров компьютера, одновременно выполняя тело цикла для всех значений его параметров, дают результат, эквивалентный результату, полученному при последовательном выполнении цикла одним процессором. В этом случае говорят, что итерации цикла независимы. Так что цикл допускает распараллеливание, если итерации цикла независимы. Если цикл может быть распараллелен, то при наличии нескольких процессоров появляется потенциальная возможность ускорить выполнение алгоритма за счет того, что процессоры будут выполнять тело цикла параллельно.

Приведенное выше определение распараллеливания неконструктивно. Условия, при выполнении которых цикл может быть распараллелен, достаточно сложны. Мы ограничимся рассмотрением примеров, для каждого из которых будем пояснять, почему тот или иной цикл может или не может быть распараллелен.