|
не хватает одного параметра: static void Main(string[] args) |
Параллельные алгоритмы
Вычисление тригонометрических функций
Сходящиеся ряды появляются во многих приложениях. В частности вычисление многих функций основано на использовании их разложения в сходящийся ряд. Рассмотрим задачу вычисления значения непрерывной дифференцируемой функции, используя ее разложение в ряд Тэйлора.
С программистской точки зрения задача сводится к вычислению бесконечной суммы сходящегося ряда:
 |
( 3.5) |
При построении эффективного последовательного алгоритма, как правило, удается построить рекуррентную формулу, существенно снижающую трудоемкость вычислений
 |
( 3.6) |
Учитывая сходимость 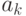 , бесконечная сумма заменяется конечной суммой, когда суммирование заканчивается при условии, что
, бесконечная сумма заменяется конечной суммой, когда суммирование заканчивается при условии, что 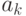 по модулю становится меньше заданной точности вычислений
по модулю становится меньше заданной точности вычислений  . В другом варианте задаются достаточно большим значением N и вычисления прекращаются при i равном N.
. В другом варианте задаются достаточно большим значением N и вычисления прекращаются при i равном N.
Как распараллелить вычисление суммы? Понятно, что при наличии параллельно работающих P процессоров, каждый из них может вычислять свою часть суммы:
 |
( 3.7) |
Если при суммировании задавать N и выбирать его кратным P (N = k * P), то каждый из процессоров может вычислять k членов суммы. Например, первый процессор будет вычислять сумму первых k членов, второй - суммирует следующую группу из k членов и так далее. Этот алгоритм распараллеливания мы называем сегментным алгоритмом. Другой способ распараллеливания вычислений, называемый шаговым алгоритмом, состоит в том, что процессоры суммируют члены ряда, отстоящие друг от друга на расстоянии P.
Последовательный алгоритм зачастую имеет несомненные достоинства, состоящие в том, что во многих практически значимых задачах удается построить простую рекуррентную формулу для вычисления 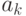 и простую формулу для вычисления начального члена суммы. Поскольку вычисление
и простую формулу для вычисления начального члена суммы. Поскольку вычисление 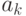 может требовать сложных вычислений, то применение простых рекуррентных соотношений позволяет существенно увеличить эффективность последовательного алгоритма. При применении сегментного алгоритма распараллеливания удается сохранить рекуррентную формулу, применяемую в последовательном алгоритме. Однако для каждого процессора необходимо вычислить начальное значение и это существенно снижает эффект, получаемый за счет распараллеливания. Для шагового алгоритма начальные значения вычисляются не столь сложно, но рекуррентная формула становится намного сложнее. Это типичная картина - распараллеливание требует жертв - усложнения алгоритма. В результате может оказаться, что привлечение дополнительных процессоров может приводить не к снижению времени вычислений, а к его росту. В подобных задач может существовать оптимальное число процессоров p*, после достижения которого время вычислений начнет возрастать.
может требовать сложных вычислений, то применение простых рекуррентных соотношений позволяет существенно увеличить эффективность последовательного алгоритма. При применении сегментного алгоритма распараллеливания удается сохранить рекуррентную формулу, применяемую в последовательном алгоритме. Однако для каждого процессора необходимо вычислить начальное значение и это существенно снижает эффект, получаемый за счет распараллеливания. Для шагового алгоритма начальные значения вычисляются не столь сложно, но рекуррентная формула становится намного сложнее. Это типичная картина - распараллеливание требует жертв - усложнения алгоритма. В результате может оказаться, что привлечение дополнительных процессоров может приводить не к снижению времени вычислений, а к его росту. В подобных задач может существовать оптимальное число процессоров p*, после достижения которого время вычислений начнет возрастать.
Приведем пример, демонстрирующий указанные проблемы. В качестве функции f(x) выберем функцию ArcSin(x), для которой справедливо следующее разложение в ряд Тэйлора:
 |
( 3.8) |
Точная формулировка задачи состоит в следующем. Дано вещественное число x такое, что  . Требуется найти с заданной точностью значение функции ArcSin(x), вычисляемое как сумма бесконечного сходящегося ряда (3.8). Нетрудно получить следующие соотношения:
. Требуется найти с заданной точностью значение функции ArcSin(x), вычисляемое как сумма бесконечного сходящегося ряда (3.8). Нетрудно получить следующие соотношения:

 |
( 3.9) |

где k=2i+1
Последовательный алгоритм построен на шаблоне, заданном алгоритмом 3.5. Отличие состоит в том, что добавляется аргумент x и текущий член вычисляется в соответствии с рекуррентной формулой, заданной соотношением (3.9):
double x2 = x * x;
double i = 0;
double a = x; //начальное значение
double k = 0;
S = 0;
while (Math.Abs(a) > eps)
{
S += a;
k = 2 * i + 1;
a *= k * k * x2 / ((k + 1) * (k + 2));
i++;
}
Листинг
3.7.
Последовательный алгоритм вычисления функции Arcsin(x)
Шаговый алгоритм можно строить на основе шаблона, заданного алгоритмом 3.6. Нужно лишь корректно задать начальные значения и применить для вычисления общего члена рекуррентную формулу, связывающую i-й и i+p -й члены ряда. Для функции Arcsin(x) эта формула имеет вид:
 |
( 3.10) |
Вот код соответствующего алгоритма:
double x2 = x * x;
double i = 0;
double k = 0;
double[] y = new double[count_p];
double a = 0;
double x2p = x2;
//Вычисление начальных значений
y[0] = x;
for (int j = 1; j < count_p; j++)
{
k = 2 * i + 1;
y[j] = y[j - 1] * k * k * x2 / ((k + 1) * (k + 2));
i++;
x2p *= x2;
}
for(int j = 0; j < count_p; j++)
{
a = y[j];
i = 0;
double pr = 1;
while (Math.Abs(a) > eps)
{
pr = 1;
for(int r = 1; r <= count_p; r++)
pr *= (1- 1/(2*(i + r)));
a *= pr * (2*i + 1)/((2*(i +count_p) +1)) * x2p;
y[j] += a;
i += count_p;
}
}
S = y[0];
for (int j = 1; j < count_p; j++)
S += y[j];
Листинг
3.8.
Шаговый алгоритм вычисления функции Arcsin(x)
Конечно формула (3.10) существенно сложнее, чем формула (3.9) для последовательного алгоритма. Это плата за распараллеливание, которая может оказаться чрезмерной в ряде случаев. Результаты численных экспериментов для данной конкретной функции будут приведены в последующих главах.
Для сегментного алгоритма рекуррентное соотношение дается формулой (3.9), как и для последовательного алгоритма. Но вычисление начального значения для соответствующего сегмента потребует серьезных вычислительных затрат в сравнении с последовательным алгоритмом. Поэтому для задач, подобных вычислению функции ArcSin(x), использование p процессоров не даст выигрыша во времени в p раз. Не буду приводить код сегментного алгоритма, полагая, что он достаточно понятен.
