НОУ ИНТУИТ | Параллельные вычисления и многопоточное программирование. Лекция 4: Параллельные алгоритмы

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 23.04.2013 | Доступ: свободный | Студентов: 854 / 185 | Длительность: 12:54:00

Темы: Программирование, Суперкомпьютерные технологии

Теги: c#, высокопроизводительные вычисления, кластеры, многозадачность, распараллеливание

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать курс

| Скачать электронную книгу

Алгоритм сортировки "Чет - Нечет"

Алгоритм представляет вариацию алгоритма пузырьковой сортировки. В последовательном варианте он применяется редко, поскольку он сложнее и интуитивно менее понятен, чем алгоритм пузырька. Интересен он тем, что допускает естественное распараллеливание. Как и в алгоритме пузырька внешний цикл задает n проходов по сортируемому массиву. На каждом проходе, как и в алгоритме пузырька, происходит сравнение и обмен двух соседних элементов. Но есть два важных отличия:

на каждом проходе производится n/2 независимых сравнений соседних пар, так что никакой элемент пары не участвует в дальнейших сравнениях на данном проходе;
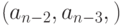Проходы делятся на четные и нечетные. На четных проходах обмен начинается с пары $(a_{n-1}, a_{n-2},)$ . На нечетном проходе производится сдвиг и начальной парой является пара $(a_{n-2}, a_{n-3},)$ . (Предполагается, что нумерация элементов массива начинается с нуля).

В отличие от "пузырька", где на i -м проходе первые i элементов занимают свои места, в алгоритме "чет - нечет" элементы гарантировано занимают свои места после выполнения всех n проходов. Для самого легкого элемента достаточно n - 1 проход для "всплытия" в вершину массива, так как на каждом проходе элемент поднимается вверх на одну позицию. Для следующего за ним элемента может понадобиться в самом неблагоприятном случае ровно N проходов. На первом проходе элемент может опуститься на последнее место (например в случае инверсного массива), на втором проходе остаться на последнем месте, поскольку не будет участвовать в сравнениях, а затем начнет подниматься и за n - 2 прохода станет на свое место. Не буду проводить формального доказательства корректности алгоритма для всех элементов, приведу реализацию алгоритма:

/// <summary>
        /// Чет-нечет сортировка
        /// Вариация пузырьковой сортировки
        /// </summary>
        public void OddEvenSortSeq()
        {
            int n = mas.Length;
            int m = n/2;
            double temp = 0;
            for (int k = 0; k < n; k++)
            { //цикл по числу проходов               
                if (k % 2 == 0)                
                    for (int j = n - 1; j > 0; j -= 2)
                    {
                        if (mas[j] < mas[j - 1])
                        {
                            temp = mas[j];
                            mas[j] = mas[j - 1];
                            mas[j - 1] = temp;
                        }
                    }                
                else
                    for (int j = n - 2; j > 0; j -= 2)
                    {
                        if (mas[j] < mas[j - 1])
                        {
                            temp = mas[j];
                            mas[j] = mas[j - 1];
                            mas[j - 1] = temp;
                        }
                    }
            }
        }

Как уже говорилось, достоинство этого алгоритма в том, что итерации внутренних циклов независимы и потому допускают естественное распараллеливание. Приведенный алгоритм можно рассматривать и как параллельный алгоритм. Внутренние циклы for без труда могут быть заменены на циклы Parallel.for, о которых будет рассказано в последующих главах.

В идеальном случае, когда все итерации внутренних циклов выполняются параллельно, что достижимо на метакомпьютере или хорошем суперкомпьютере, параллельный алгоритм имеет линейную сложность O(n), что позволяет считать этот алгоритм одним из лучших. На практике ситуация не столь радужная. Дело в том, что в реализациях, основанных на потоках, придется создавать большое число потоков - 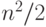n^2/2 , каждый из которых выполняет не более 10 команд процессора, требуемых для сравнения и обмена одной пары элементов массива. Накладные расходы при этом столь велики, что могут съесть весь выигрыш, полученный за счет распараллеливания. Поэтому в практически полезных реализациях необходимо разбивать сортируемый массив на p фрагментов, переходя к длинным итерациям.

Быстрая сортировка Хоара

В заключение этой главы рассмотрим быструю сортировку Хоара. Идея распараллеливания такая же, как и в методе пузырьковой сортировки. Распараллеливание идет по данным. Исходный массив разбивается на фрагменты. Однако здесь, в отличие от пузырьковой сортировки, используется сегментное деление. К каждому фрагменту применяется последовательный алгоритм, а затем выполняется слияние отсортированных фрагментов. Cложность параллельного варианта быстрой сортировки задается соотношением O(n/p*log(n/p)+n*p).

Вот текст соответствующих методов на C# - последовательной и параллельной версий:

/// <summary>
        /// Быстрая сортировка Хоара
        /// Вызов рекурсивной версии
        /// </summary>
        /// <param name="mas"></param>
        public void QuickSort(double[] mas)
        {
            QSort(mas, 0, mas.Length - 1);
        }

        /// <summary>
        /// Рекурсивная версия быстрой сортировки
        /// </summary>
        /// <param name="mas">сортируемый массив</param>
        /// <param name="start">индекс начала сортируемой части</param>
      /// <param name="finish">индекс конца сортируемой части массива </param>
        void QSort(double[] mas, int start, int finish)
        {
           
            if (finish - start > 0)
            {
                double cand = 0, temp = 0;
                int l = start, r = finish;
                cand = mas[(r + l) / 2];
                while (l <= r)
                {
                    while (mas[l] < cand) l++;
                    while (mas[r] > cand) r--;
                    if (l <= r)
                    {
                        temp = mas[l];
                        mas[l] = mas[r];
                        mas[r] = temp;
                        l++; r--;
                    }
                }
                QSort(mas, start, r);
                QSort(mas, l, finish);
            }
        }
        /// <summary>
        /// Быстрая сортировка Хоара
        /// Параллельная версия
        /// </summary>
        /// <param name="mas"></param>
        /// <param name="p">число процессоров</param>
        public void QuickSortParallel(double[] mas, int p)
        {
            int n = mas.Length;
            int m = n / p;
            for (int i = 0; i < p; i++)
            {
                int start = i * m;
                int finish = i != p - 1? start + m - 1 : n - 1;
                QSort(mas, start, finish);                
            }//Слияние             
          //MergeQ(mas, p);
            MergeQ1(mas, p);
        }

        /// <summary>
        /// Слияние упорядоченных последовательностей
        /// Последовательности представляют подряд идущие отрезки
        /// Используется дополнительная память
        /// </summary>
        /// <param name="mas">сортируемый массив</param>
        /// <param name="p">число процессоров</param>
        public void MergeQ1(double[] mas, int p)
        {
            int n = mas.Length;
            int m = n / p;
            int index_min = 0;            
            double min = 0;            
            int i = 0;
            double[] tmas = new double[n];
            int[] start = new int[p], finish = new int[p];
            for (i = 0; i < p; i++)
            {
                start[i] = i * m;
                finish[i] = i != p - 1 ? start[i] + m - 1 : n - 1;
            }
            for (int k = 0; k < n; k++)
            {//пересылка k-ого элемента
                //поиск кандидата
                i = 0;
                while (start[i] > finish[i]) i++;
                index_min = i; min = mas[start[i]]; 
                    
                for (int j = i+1; j < p; j++)
                {
                    //цикл по кандидатам
                    if (start[j] <= finish[j])
                    {
                        if (mas[start[j]] < min)
                        {
                            min = mas[start[j]];
                            index_min = j;                            
                        }
                    }
                }                    
                    //pass                        
                        tmas[k] = mas[start[index_min]];
                        start[index_min]++;
            }
            for (i = 0; i < n; i++)
                mas[i] = tmas[i];
        }
    }
}

Приведу таблицу, в которой указано время выполнения различных вариантов сортировки на одном и том же массиве из 10 000 элементов типа double. Время задается в тиках. Для уменьшения погрешности время указывается для многократного решения задачи сортировки массива. Число повторов равно 10. Число процессоров, указываемых для параллельных вариантов равно 8.

Таблица 3.2. Время сортировки массива разными методами
Метод	BubbleClassic	Bubble_1	Bubble_2	BubbleParallel	QSort	QParallel
Время	48132753	50622896	51762960	6780388	180010	250014

Во всех случаях выполнение шло последовательно. Потенциально параллельные алгоритмы допускают распараллеливание, но реально оно не выполнялось. Тем не менее, параллельный алгоритм пузырьковой сортировки значительно эффективнее (хотя и сложнее) классических последовательных вариантов алгоритма. Для быстрой сортировки последовательная версия показывает лучшие результаты, чем параллельная.

Дальше >>

Авторизоваться

Параллельные вычисления и многопоточное программирование

Параллельные алгоритмы

Алгоритм сортировки "Чет - Нечет"

Быстрая сортировка Хоара

Вопросы и ответы