Трансфинитная индукция

Теорема 19. Пусть отображение , о котором шла речь в теореме 18, является частичным (для некоторых и функций 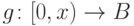оно может быть не определено). Тогда существует функция , которая

• либо определена на всем и согласована с рекурсивным определением;
• либо определена на некотором начальном отрезке 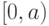и на нем согласована с рекурсивным определением, причем для точки и функции рекурсивное правило неприменимо (отображение не определено).

Доказательство. Это утверждение является обобщением, но одновременно и следствием предыдущей теоремы 18. В самом деле, добавим к множеству специальный элемент 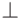(" неопределенность") и модифицируем рекурсивное правило: новое правило дает значение 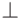, когда старое было не определено. (Если среди значений функции на предыдущих аргументах уже встречалось 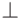, новое рекурсивное правило тоже дает .)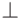

Применив теорему 18 к модифицированному правилу, получим некоторую функцию 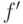. Если эта функция нигде не принимает значения 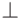, то реализуется первая из двух возможностей, указанных в теореме (при 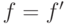). Если же функция 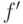принимает значение 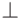в какой-то точке, то она имеет то же значени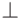е и во всех больших точках. Заменив значение 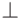на неопределенность, мы получаем из функции 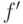функцию . Область определения функции есть некоторый начальный отрезок 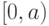и реализуется вторая возможность, указанная в формулировке теоремы.

114.Сформулируйте и докажите утверждение об однозначности функции, заданной частичным рекурсивным правилом.

Теперь у нас все готово для доказательства теоремы о сравнении вполне упорядоченных множеств.

Теорема. Пусть и - два вполне упорядоченных множества. Тогда либо изоморфно некоторому начальному отрезку множества , либо изоморфно некоторому начальному отрезку множества .

Доказательство. Отметим прежде всего, что начальный отрезок может совпадать со всем множеством, так что случай изоморфных множеств и также покрывается этой теоремой.

Определим отображение из в таким рекурсивным правилом: для любого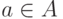

есть наименьший элемент множества , который не встречается среди при .

Это правило не определено в том случае, когда значения 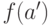при 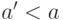покрывают все . Применяя теорему 19, мы получаем функцию , согласованную с этим правилом. Теперь рассмотрим два случая:

• Функция определена на всем . Заметим, что рекурсивное определение гарантирует монотонность, поскольку 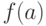определяется как минимальный еще не использованный элемент; чем больше , тем меньше остается неиспользованных элементов и потому минимальный элемент может только возрасти (из определения следует также, что одинаковых значений быть не может). Остается лишь проверить, что множество значений функции , то есть 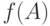, будет начальным отрезком. 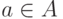В самом деле, пусть для некоторого ; надо проверить, что также является значением функции . 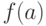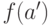Действительно, согласно рекурсивному определению является наименьшим неиспользованным значением, следовательно, уже использовано, то есть встречается среди при .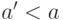
• Функция определена лишь на некотором начальном отрезке 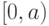. В этом случае этот начальный отрезок изоморфен , и функция является искомым изоморфизмом. В самом деле, раз 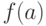не определено, то среди значений функции встречаются все элементы множества . С другой стороны, сохраняет порядок в силу рекурсивного определения.

Таким образом, в обоих случаях утверждение теоремы верно.

Может ли быть так, что изоморфно начальному отрезку , а изоморфно начальному отрезку ? Нет - за исключением тривиального случая, когда начальные отрезки представляют собой сами множества и . Это вытекает из такого утверждения:

Теорема 21. Никакое вполне упорядоченное множество не изоморфно своему начальному отрезку (не совпадающему со всем множеством).

Доказательство. Пусть вполне упорядоченное множество изоморфно своему начальному отрезку, не совпадающему со всем множеством. Как мы видели на с. 67, этот отрезок имеет вид 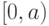для некоторого элемента 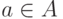. Пусть 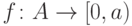- изоморфизм. Тогда строго возрастает, и по теореме 17 имеет место неравенство 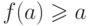, что противоречит тому, что множество значений функции есть .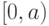

Если множество изоморфно начальному отрезку множества , а множество изоморфно начальному отрезку множества , то композиция этих изоморфизмов дает изоморфизм между множеством и его начальным отрезком (начальный отрезок начального отрезка есть начальный отрезок). Этот начальный отрезок обязан совпадать со всем множеством , так что это возможно лишь если и изоморфны.

Сказанное позволяет сравнивать вполне упорядоченные множества. Если изоморфно начальному отрезку множества , не совпадающему со всем , то говорят, что порядковый тип множества меньше порядкового типа множества . Если множества и изоморфны, то говорят, что у них одинаковые порядковые типы. Наконец, если изоморфно начальному отрезку множества , то говорят, что порядковый тип множества больше порядкового типа множества . Как мы только что доказали, верно такое утверждение:

Теорема 22. Для любых вполне упорядоченных множеств и имеет место ровно один из указанных трех случаев.

Если временно забыть о проблемах оснований теории множеств и определить порядковый тип упорядоченного множества как класс изоморфных ему упорядоченных множеств, то можно сказать, что мы определили линейный порядок на порядковых типах вполне упорядоченных множеств (на ординалах, как говорят). Этот порядок будет полным. Мы переформулируем это утверждение так, чтобы избегать упоминания классов.

Теорема 23. Всякое непустое семейство вполне упорядоченных множеств имеет " наименьший элемент" - множество, изоморфное начальным отрезкам всех остальных множеств.

Доказательство. Возьмем какое-то множество семейства. Если оно наименьшее, то все доказано. Если нет, рассмотрим все множества семейства, которые меньше его, то есть изоморфны его начальным отрезкам вида 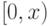. Среди всех таких элементов выберем наименьший. Тогда соответствующее ему множество и будет наименьшим.

Следствием доказанных теорем является то, что любые два вполне упорядоченных множества сравнимы по мощности (одно равномощно подмножеству другого). Сейчас мы увидим, что всякое множество может быть вполне упорядочено (теорема Цермело), и, следовательно, любые два множества сравнимы по мощности.