Теорема Кантора
Теорема 8. (общая формулировка теоремы Кантора)
Никакое множество 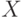 не равномощно множеству всех своих
подмножеств.
не равномощно множеству всех своих
подмножеств.
Доказательство.
Пусть 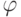 - взаимно однозначное соответствие
между
- взаимно однозначное соответствие
между 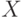 и
множеством
и
множеством 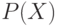 всех подмножеств множества
всех подмножеств множества 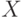 .
Рассмотрим те
элементы
.
Рассмотрим те
элементы  , которые не принадлежат соответствующему им
подмножеству.
Пусть
, которые не принадлежат соответствующему им
подмножеству.
Пусть 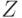 - образованное ими множество:
- образованное ими множество:
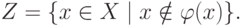
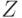 не соответствует никакому
элементу множества
не соответствует никакому
элементу множества 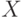 . Пусть это не так и
. Пусть это не так и  для некоторого
элемента
для некоторого
элемента 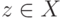 . Тогда
. Тогда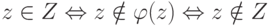
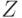 , второе - по предположению
, второе - по предположению 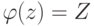 ). Полученное противоречие показывает, что
). Полученное противоречие показывает, что 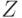 действительно ничему не соответствует, так что
действительно ничему не соответствует, так что 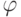 не взаимно однозначно.
не взаимно однозначно.С другой, стороны, любое множество 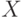 равномощно некоторой
части множества
равномощно некоторой
части множества 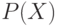 . В самом деле, каждому
элементу
. В самом деле, каждому
элементу 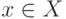 можно
поставить в соответствие одноэлементное подмножество
можно
поставить в соответствие одноэлементное подмножество  .
Поэтому, вспоминая определение сравнения множеств по мощности
, можно сказать, что мощность
множества
.
Поэтому, вспоминая определение сравнения множеств по мощности
, можно сказать, что мощность
множества 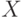 всегда меньше мощности множества
всегда меньше мощности множества 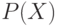
58. Докажите, что  для всех натуральных
для всех натуральных 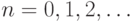
В общей формулировке теорема 8 появляется в работе Кантора
1890/91 года. Вместо подмножеств Кантор говорит о функциях,
принимающих значения  и
и  .
.
На самом деле мы уже приблизились к опасной границе, когда
наглядные представления о множествах приводят к противоречию. В
самом деле, рассмотрим множество всех множеств 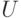 , элементами
которого являются все множества. Тогда, в частности, все
подмножества множества
, элементами
которого являются все множества. Тогда, в частности, все
подмножества множества 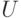 будут его элементами,
и
будут его элементами,
и 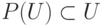 , что невозможно по теореме Кантора.
, что невозможно по теореме Кантора.
Это рассуждение можно развернуть, вспомнив доказательство теоремы Кантора - получится так называемый парадокс Рассела. Вот как его обычно излагают.
Типичные множества не являются своими
элементами. Скажем, множество натуральных чисел  само не является натуральным числом и потому не будет своим
элементом. Однако в принципе можно себе представить и
множество, которое является своим элементом (например, множество
всех множеств). Назовем такие множества " необычными".
Рассмотрим теперь множество всех обычных множеств. Будет
ли оно обычным? Если оно обычное, то оно является своим
элементом и потому необычное, и наоборот. Как же так?
само не является натуральным числом и потому не будет своим
элементом. Однако в принципе можно себе представить и
множество, которое является своим элементом (например, множество
всех множеств). Назовем такие множества " необычными".
Рассмотрим теперь множество всех обычных множеств. Будет
ли оно обычным? Если оно обычное, то оно является своим
элементом и потому необычное, и наоборот. Как же так?
Модифицированная версия этого парадокса такова: будем называть прилагательное самоприменимым, если оно обладает описываемым свойством. Например, прилагательное " русский" самоприменимо, а прилагательное " глиняный" нет. Другой пример: прилагательное " трехсложный" самоприменимо, а " двусложный" нет. Теперь вопрос: будет ли прилагательное " несамоприменимый" самоприменимым? (Любой ответ очевидно приводит к противоречию.)
Отсюда недалеко до широко известного " парадокса лжеца ", говорящего " я лгу", или до истории о солдате, который должен был брить всех солдат одной с ним части, кто не бреется сам и т.п.
Возвращаясь к теории множеств, мы обязаны дать себе отчет в том, что плохого было в рассуждениях, приведших к парадоксу Рассела. Вопрос этот далеко не простой, и его обсуждение активно шло всю первую половину 20- го века. Итоги этого обсуждения приблизительно можно сформулировать так:
- Понятие множества не является непосредственно очевидным; разные люди (и научные традиции) могут понимать его по- разному.
- Множества - слишком абстрактные объекты для того, чтобы
вопрос " а что на самом деле?" имел смысл. Например,
в работе Кантора 1878 года была сформулирована континуум-
гипотеза: всякое подмножество отрезка либо
конечно, либо
счетно, либо равномощно всему отрезку. (Другими словами,
между счетными множествами и множествами
мощности континуум нет промежуточных мощностей). Кантор написал, что это
может быть доказано " с помощью некоторого метода индукции, в
изложение которого мы не будем входить здесь подробнее", но на
самом деле доказать это ему не удалось. Более того, постепенно
стало ясно, что утверждение континуум- гипотезы можно считать
истинным или ложным, - при этом получаются разные теории
множеств, но в общем- то ни одна из этих теорий не лучше
другой.
Тут есть некоторая аналогия с неевклидовой геометрией. Мы можем считать " пятый постулат Евклида " (через данную точку проходит не более одной прямой, параллельной данной) истинным. Тогда получится геометрия, называемая евклидовой. А можно принять в качестве аксиомы противоположное утверждение: через некоторую точку можно провести две различные прямые, параллельные некоторой прямой. Тогда получится неевклидова геометрия. [Отметим, кстати, распространенное заблуждение: почему- то широкие массы писателей о науке и даже отдельные математики в минуты затмений (см. статью в Вестнике Академии Наук, посвященную юбилею Лобачевского) считают, что в неевклидовой геометрии параллельные прямые пересекаются. Это не так - параллельные прямые и в евклидовой, и в неевклидовой геометрии определяются как прямые, которые не пересекаются.]
Вопрос о том, евклидова или неевклидова геометрия правильна " на самом деле", если вообще имеет смысл, не является математическим - скорее об этом следует спрашивать физиков. К теории множеств это относится в еще большей степени, и разве что теология (Кантор неоднократно обсуждал вопросы теории множеств с профессионалами - теологами) могла бы в принципе претендовать на окончательный ответ.
- Если мы хотим рассуждать о множествах, не впадая в противоречия, нужно проявлять осторожность и избегать определенных видов рассуждений. Безопасные (по крайней мере пока не приведшие к противоречию) правила обращения со множествами сформулированы в аксиоматической теории множеств (формальная теория ZF, названная в честь Цермело и Френкеля). Добавив к этой теории аксиому выбора, получаем теорию, называемую ZFC (сhoice по-английски - выбор). Есть и другие, менее популярные теории.
Однако формальное построение теории множеств выходит за рамки нашего обсуждения. Поэтому мы ограничимся неформальным описанием ограничений, накладываемых во избежание противоречий: нельзя просто так рассмотреть множество всех множеств или множество всех множеств, не являющихся своими элементами, поскольку класс потенциальных претендентов слишком " необозрим". Множества можно строить лишь постепенно. Например, можно образовать множество всех подмножеств данного множества ( аксиома степени ). Можно рассмотреть подмножество данного множества, образованное элементами с каким- то свойством ( аксиома выделения ). Можно рассмотреть множество всех элементов, входящих хотя бы в один из элементов данного множества ( аксиома суммы ). Есть и другие аксиомы.
Излагая сведения из теории множеств, мы будем стараться держаться подальше от опасной черты, и указывать на опасность в тех местах, когда возникнет искушение к этой черте приблизиться. Пока что такое место было одно: попытка определить мощность множества как класс (множество) всех равномощных ему множеств.
