Множества
Равномощные множества
Два множества называют равномощными, если между ними можно установить взаимно однозначное соответствие, при котором каждому элементу одного множества соответствует ровно один элемент другого.
Для конечных множеств это означает, что в них одинаковое число
элементов, но определение имеет смысл и для бесконечных
множеств. Например, отрезки ![[0,1]](/sites/default/files/tex_cache/ccfcd347d0bf65dc77afe01a3306a96b.png) и
и ![[0,2]](/sites/default/files/tex_cache/70fd3f388413505934da60b43afc4088.png) равномощны,
поскольку отображение
равномощны,
поскольку отображение 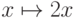 осуществляет искомое
соответствие.
осуществляет искомое
соответствие.
26. Докажите, что любые два интервала 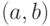 и
и  на прямой равномощны.
на прямой равномощны.
27. Докажите, что любые две окружности на плоскости равномощны. Докажите, что любые два круга на плоскости равномощны.
28. Докажите, что полуинтервал 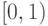 равномощен
полуинтервалу
равномощен
полуинтервалу ![(0,1]](/sites/default/files/tex_cache/668c7b55a37300c330dcd565d9e076da.png) .
.
Несколько более сложна такая задача: доказать, что интервал 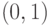 и луч
и луч 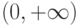 равномощны. Это делается
так. Заметим,
что отображение
равномощны. Это делается
так. Заметим,
что отображение 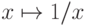 является взаимно однозначным
соответствием
между
является взаимно однозначным
соответствием
между 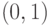 и
и 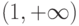 , а
, а 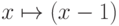 -
взаимно однозначным соответствием между
-
взаимно однозначным соответствием между 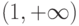 и
и 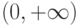 , поэтому их композиция
, поэтому их композиция 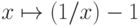 является искомым взаимно однозначным соответствием между
является искомым взаимно однозначным соответствием между 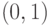 и
и 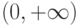 .
.
Вообще, как говорят, отношение равномощности есть отношение эквивалентности. Это
означает, что оно рефлексивно
(каждое множество равномощно самому себе), симметрично
(если  равномощно
равномощно  , то и
, то и  равномощно
равномощно  )
и транзитивно (если
)
и транзитивно (если  равномощно
равномощно  и
и  равномощно
равномощно  , то
, то  равномощно
равномощно  ). Свойством
транзитивности мы только что воспользовались, взяв луч
). Свойством
транзитивности мы только что воспользовались, взяв луч 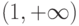 в качестве промежуточного множества.
в качестве промежуточного множества.
Еще несколько примеров:
- Множество бесконечных последовательностей нулей и единиц
равномощно множеству всех подмножеств натурального
ряда. (В самом деле, сопоставим с каждой последовательностью
множество номеров мест, на которых стоят единицы: например,
последовательность из одних нулей соответствует пустому
множеству, из одних единиц -натуральному ряду, а
последовательность
 - множеству четных чисел.)
- множеству четных чисел.) - Множество бесконечных последовательностей цифр
 ,
,  ,
,  ,
,  равномощно множеству бесконечных последовательностей цифр
равномощно множеству бесконечных последовательностей цифр  и
и  . (В самом деле, можно закодировать цифры
. (В самом деле, можно закодировать цифры  ,
,  ,
,  ,
,  группами
группами  ,
, 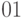 ,
,  ,
,  .
Обратное преобразование
разбивает последовательность нулей и единиц на пары,
после чего каждая пара заменяется на цифру от
.
Обратное преобразование
разбивает последовательность нулей и единиц на пары,
после чего каждая пара заменяется на цифру от  до
до  .)
.) - Множество бесконечных последовательностей цифр
 ,
,  ,
,  равномощно множеству бесконечных последовательностей цифр
равномощно множеству бесконечных последовательностей цифр  и
и  .
(Можно было бы пытаться рассуждать так: это множество заключено
между двумя множествами одной и той же мощности, и потому
равномощно каждому из них. Этот ход мыслей
правилен, как показывает теорема Кантора - Бернштейна из
"лекции 3"
.
Но здесь можно обойтись и без этой теоремы, если
закодировать цифры
.
(Можно было бы пытаться рассуждать так: это множество заключено
между двумя множествами одной и той же мощности, и потому
равномощно каждому из них. Этот ход мыслей
правилен, как показывает теорема Кантора - Бернштейна из
"лекции 3"
.
Но здесь можно обойтись и без этой теоремы, если
закодировать цифры  ,
,  и
и  последовательностями
последовательностями  ,
,  и
и  : легко сообразить, что всякая последовательность нулей и
единиц однозначно разбивается на такие блоки слева направо.
Такой способ кодирования называют " префиксным кодом"
.)
: легко сообразить, что всякая последовательность нулей и
единиц однозначно разбивается на такие блоки слева направо.
Такой способ кодирования называют " префиксным кодом"
.) - Пример с последовательностями нулей и единиц можно обобщить:
множество подмножеств любого множества
 (оно обычно
обозначается
(оно обычно
обозначается 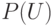 и под
английски называется power set) равномощно
множеству всех функций, которые ставят в соответствие каждому
элементу
и под
английски называется power set) равномощно
множеству всех функций, которые ставят в соответствие каждому
элементу 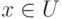 одно из чисел
одно из чисел  и
и  (множество таких
функций обычно обозначают
(множество таких
функций обычно обозначают 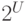 ). (В самом
деле, каждому
множеству
). (В самом
деле, каждому
множеству 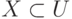 соответствует его характеристическая
функция.)
соответствует его характеристическая
функция.)
Мы продолжим этот список, но сначала полезно доказать несколько простых фактов о счетных множествах (равномощных множеству натуральных чисел).
