Лекция 3: Математическое программирование. Линейное программирование. Виды задач линейного программирования. Постановка задач линейного программирования и исследование их структуры. Решение задач линейного программирования симплекс-методом
4. Решение задач линейного программирования симплекс–методом
Симплекс-метод, известный также под названием метода последовательного улучшения плана, впервые разработал Г.Данциг в 1947 г. Этот метод позволяет переходить от одного допустимого базисного решения к другому, причем так, что значения целевой функции непрерывно возрастают. В результате оптимальное решение находят за конечное число шагов.
Алгоритмы симплекс-метода позволяют также установить, является ли задача ЛП разрешимой.
Запишем ограничения задачи ЛП в таком виде:
A1x1 + A2x2 + ... + Anxn + An+1xn+1 + ... + An+mxn+m = A0.
Пусть A1,...,Am - множество линейно независимых векторов.
Тогда уравнение
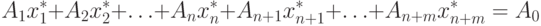 |
( 4.1) |
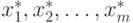 ,
,Предположим, что это решение допустимо, то есть 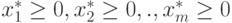 .
Базис {A1,.,Am} образует m -мерное пространство, а потому каждый из
векторов Am+1,.,Am+n
единственным образом выражается через этот базис.
Если Ar не входит в базис, то
.
Базис {A1,.,Am} образует m -мерное пространство, а потому каждый из
векторов Am+1,.,Am+n
единственным образом выражается через этот базис.
Если Ar не входит в базис, то
 |
( 4.2) |
Предположим, что хотя бы одна из величин xir больше нуля.
Решение уравнения
 |
( 4.3) |
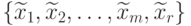
Тогда, очевидно:
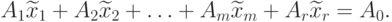 |
( 4.4) |
Умножив уравнение (4.2) на xr и вычтя полученное уравнение из уравнения (4.1), получим
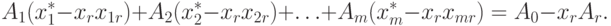 |
( 4.5) |
Сравнив уравнения (4.5) и (4.4), находим связь нового решения 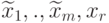 со старым базисным решением
со старым базисным решением 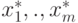 :
:
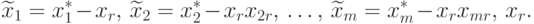 |
( 4.6) |
Решение (4.6), во-первых, не будет базисным, так как содержит m + 1 переменную, а во-вторых, будет допустимым не для всех значений xr.
Чтобы новое решение оставалось допустимым, нужно выбрать
значение xr таким, чтобы ни одна из
величин 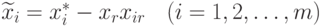 не стала меньше нуля. Следовательно, максимальное значение переменной xr определяется соотношением
не стала меньше нуля. Следовательно, максимальное значение переменной xr определяется соотношением
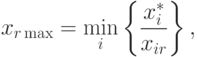 |
( 4.7) |
Чтобы сделать новое допустимое решение базисным, нужно одну переменную xi вывести из базисного решения, а соответствующий вектор из базиса. В этом случае новый базис будет содержать также m векторов.
Для этого выбираем значения в соответствии с (4.7). Тогда новое базисное решение имеет вид
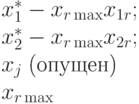
Такой переход от одного базиса к другому позволяет находить решения почти всех задач ЛП. Определив все крайние точки, можно вычислить значения целевой функции и найти оптимальное решение. Однако для больших значений m и n это практически невозможно. Поэтому для перехода от текущего решения к новому допустимому базисному решению, которому отвечает большее значение целевой функции, используют соответствующий критерий ( симплекс-разность ).
Новому ДБР 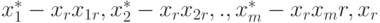 соответствует следующее значение целевой функции
соответствует следующее значение целевой функции
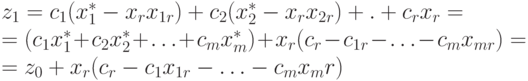 |
( 4.8) |
сr-с1x1r - с2x2r - ... - сmxmr - симплекс-разность для переменной хr.
Симплекс-разность вычисляют для каждой переменной, не входящей в базисное решение, и выбирают такую небазисную переменную хr, для которой симплекс-разность положительна и максимальна.
Таким образом, алгоритм симплекс-метода состоит из следующих этапов:
- находят начальный базис и связанное с ним допустимое базисное решение ;
- вычисляют симплекс-разность для каждой переменной, не входящей в базисное решение ;
- вводят в базис наиболее 'выгодную' переменную с максимальной
положительной симплекс-разностью ; ее значение
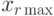 определяют из соотношениядля всех xir > 0 ;
определяют из соотношениядля всех xir > 0 ;
- выводят из базисного решения переменную xj, соответствующуюа из базиса - вектор Aj ;
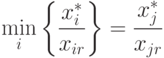
- переходят к этапу 2 новой итерации.
Этапы 2 - 4 повторяют до тех пор, пока симплекс-разности для всех переменных, не входящих в базис, не станут отрицательными.
Это и есть признак оптимальности текущего базисного решения.
