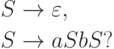|
Упражнение 2.1.25 |
Алгоритмически неразрешимые проблемы
16.4. Проблема автоматности
Лемма 16.4.1. Пусть 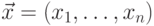 ,
,  , где
, где  ,
, 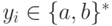 и
и 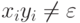 для всех i. Тогда язык
для всех i. Тогда язык 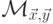 является автоматным
в том и только том случае,
когда постовская система соответствия
является автоматным
в том и только том случае,
когда постовская система соответствия 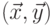 не имеет решений.
не имеет решений.
Доказательство
Пусть 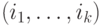 -
решение постовской системы соответствия
-
решение постовской системы соответствия 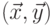 ,
где
,
где 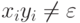 для всех i.
Положим
для всех i.
Положим
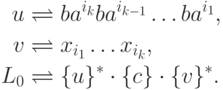
 ,
,  и
язык L0
является автоматным.
Очевидно, что
и
язык L0
является автоматным.
Очевидно, что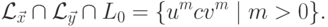
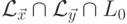 не является автоматным.
Согласно теореме 3.2.1
язык
не является автоматным.
Согласно теореме 3.2.1
язык 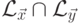 не является автоматным.
Следовательно, и язык
не является автоматным.
Следовательно, и язык 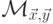 не является автоматным.
не является автоматным.Обратно, если
постовская система соответствия 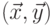 не имеет решений, то
не имеет решений, то 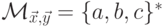 ,
а этот язык является автоматным.
,
а этот язык является автоматным.
Теорема 16.4.2. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом 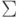 узнать, является ли автоматным язык L(G).
узнать, является ли автоматным язык L(G).
Доказательство
Докажем утверждение теоремы для случая 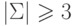 .
Из леммы 16.4.1 следует, что
если бы проблема распознавания автоматности
языка L(G)
для контекстно-свободных грамматик
над алфавитом
.
Из леммы 16.4.1 следует, что
если бы проблема распознавания автоматности
языка L(G)
для контекстно-свободных грамматик
над алфавитом 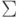 была разрешима, то также была бы разрешима
проблема соответствий Поста для
постовских систем соответствия
была разрешима, то также была бы разрешима
проблема соответствий Поста для
постовских систем соответствия  ,
где
,
где  ,
, 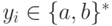 и
и 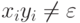 для всех i.
Но тогда была бы разрешима проблема соответствий Поста для всех
постовских систем соответствия над алфавитом {a,b}
(если
для всех i.
Но тогда была бы разрешима проблема соответствий Поста для всех
постовских систем соответствия над алфавитом {a,b}
(если 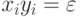 для некоторого i,
то рассматриваемая
постовская система соответствия имеет решение,
а именно (i) ).
для некоторого i,
то рассматриваемая
постовская система соответствия имеет решение,
а именно (i) ).
Упражнение 16.4.3. Является ли автоматным язык, порождаемый грамматикой
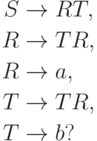
Упражнение 16.4.4. Является ли автоматным язык, порождаемый грамматикой
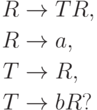
Упражнение 16.4.5. Является ли автоматным язык, порождаемый грамматикой
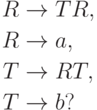
Упражнение 16.4.6. Является ли автоматным язык, порождаемый грамматикой
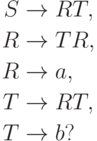
16.5. Проблемы контекстной свободности
Определение 16.5.1.
Пусть 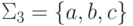 ,
, 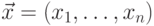 ,
,  ,
где
,
где  и
и 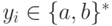 для всех i.
Обозначим через
для всех i.
Обозначим через 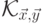 язык
язык 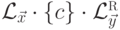 .
.
Лемма 16.5.2.
Язык 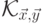 является контекстно-свободным
при любых
является контекстно-свободным
при любых 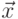 и
и 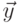 .
.
Доказательство Утверждение следует из теорем 9.4.4 и 9.4.2.
Лемма 16.5.3. Рассмотрим алфавит 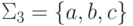 . Пусть
. Пусть 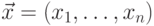 и
и  , где
, где  ,
, 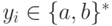 и
и 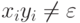 для всех i. Тогда язык
для всех i. Тогда язык 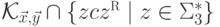 является контекстно-свободным
в том и только том случае,
когда
постовская система соответствия
является контекстно-свободным
в том и только том случае,
когда
постовская система соответствия 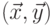 не имеет решений.
не имеет решений.
Доказательство.
Пусть 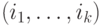 -
решение постовской системы соответствия
-
решение постовской системы соответствия 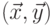 ,
где
,
где 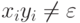 для всех i.
Положим
для всех i.
Положим
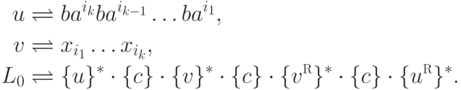
 ,
,  и
язык L0
является автоматным.
Очевидно,
что
и
язык L0
является автоматным.
Очевидно,
что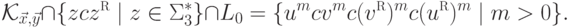
 не является контекстно-свободным.
Согласно теореме 9.6.1
язык
не является контекстно-свободным.
Согласно теореме 9.6.1
язык 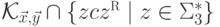 также не~является контекстно-свободным.
также не~является контекстно-свободным.Обратно, если
постовская система соответствия 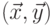 не имеет решений,
то
не имеет решений,
то 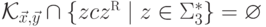 .
.
Теорема 16.5.4. Пусть  . Тогда не существует алгоритма, позволяющего по произвольным
контекстно-свободным грамматикам G1 и G2 над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольным
контекстно-свободным грамматикам G1 и G2 над алфавитом 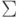 узнать, является ли контекстно-свободным язык
узнать, является ли контекстно-свободным язык 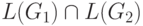 .
.
Доказательство.
Достаточно построить по постовской системе соответствия 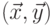 ,
где
,
где 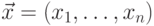 ,
,  и
для всех i
выполняется
и
для всех i
выполняется  ,
, 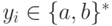 и
и 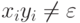 ,
контекстно-свободную грамматику G1,
порождающую язык
,
контекстно-свободную грамматику G1,
порождающую язык 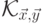 ,
и
контекстно-свободную грамматику G2,
порождающую язык
,
и
контекстно-свободную грамматику G2,
порождающую язык  .
С учетом
леммы 16.5.3
неразрешимость рассматриваемой задачи сводится к неразрешимости
проблемы соответствий Поста рассуждением,
аналогичным приведенному в доказательстве теоремы 16.4.2.
.
С учетом
леммы 16.5.3
неразрешимость рассматриваемой задачи сводится к неразрешимости
проблемы соответствий Поста рассуждением,
аналогичным приведенному в доказательстве теоремы 16.4.2.
Лемма 16.5.5. Рассмотрим алфавит 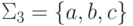 . Язык
. Язык 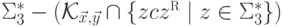 является контекстно-свободным при любых
является контекстно-свободным при любых 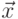 и
и 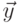 .
.
Доказательство.
Положим  .
Язык
.
Язык 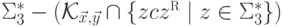 можно представить в виде объединения пяти
контекстно-свободных языков
можно представить в виде объединения пяти
контекстно-свободных языков
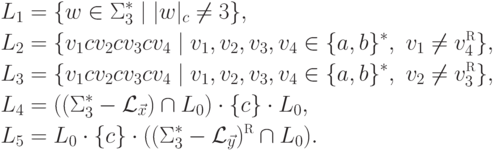
Теорема 16.5.6. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной
контекстно-свободной грамматике G над алфавитом 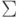 узнать, является ли контекстно-свободным язык
узнать, является ли контекстно-свободным язык 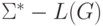 .
.
Доказательство.
Рассмотрим алфавит 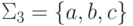 .
Достаточно построить по постовской системе соответствия
.
Достаточно построить по постовской системе соответствия 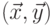 ,
где
,
где 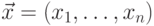 ,
,  и
для всех i
выполняется
и
для всех i
выполняется  ,
, 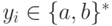 и
и 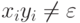 ,
контекстно-свободную грамматику G,
порождающую язык
,
контекстно-свободную грамматику G,
порождающую язык 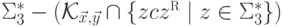 .
С учетом леммы 16.5.5
неразрешимость рассматриваемой задачи сводится к~неразрешимости
проблемы соответствий Поста рассуждением,
аналогичным приведенному в доказательстве теоремы 16.4.2.
.
С учетом леммы 16.5.5
неразрешимость рассматриваемой задачи сводится к~неразрешимости
проблемы соответствий Поста рассуждением,
аналогичным приведенному в доказательстве теоремы 16.4.2.
Лемма 16.5.7. Рассмотрим алфавит 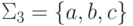 . Язык
. Язык 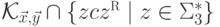 является контекстным при любых
является контекстным при любых 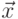 и
и 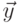 .
.
Теорема 16.5.8. Пусть  . Тогда не существует алгоритма, позволяющего по произвольной
контекстной грамматике G над алфавитом
. Тогда не существует алгоритма, позволяющего по произвольной
контекстной грамматике G над алфавитом 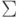 узнать, является ли контекстно-свободным язык L(G).
узнать, является ли контекстно-свободным язык L(G).
Доказательство.
Достаточно построить по постовской системе соответствия 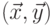 ,
где
,
где 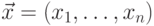 ,
,  и
для всех i
выполняется
и
для всех i
выполняется  ,
, 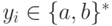 и
и 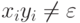 ,
контекстную грамматику G,
порождающую язык
,
контекстную грамматику G,
порождающую язык 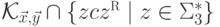 .
.
Упражнение 16.5.9.
Является ли контекстно-свободным язык  ,
где язык L
порождается грамматикой
,
где язык L
порождается грамматикой