|
Упражнение 2.1.25 |
Синтаксический разбор
В этой лекции даются формальные определения,
связанные с прямыми
(то есть читающими входную строку слева направо)
синтаксическими анализаторами.
В первом разделе доказывается, что для языков
из класса LL(1) можно построить
основанный на детерминированном автомате
с магазинной памятью
анализатор,
который создает
дерево разбора,
двигаясь снизу вверх, то есть от листьев к корню
(в теории контекстно-свободных грамматик
принято изображать деревья с корнем наверху).
Во втором разделе формулируется аналогичный результат
об анализе сверху вниз
для грамматик из класса 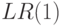 .
При этом понятие анализа снизу вверх формализовано
в терминах последовательности правил, примененных
в левостороннем выводе,
а понятие анализа сверху вниз -
в терминах обращенной последовательности правил, примененных
в правостороннем выводе.
.
При этом понятие анализа снизу вверх формализовано
в терминах последовательности правил, примененных
в левостороннем выводе,
а понятие анализа сверху вниз -
в терминах обращенной последовательности правил, примененных
в правостороннем выводе.
13.1. Нисходящий разбор
Определение 13.1.1. Процесс нахождения дерева вывода слова w в заданной контекстно-свободной грамматике называется синтаксическим разбором или синтаксическим анализом (parsing).
Определение 13.1.2. Протоколом
левостороннего вывода в контекстно-свободной грамматике 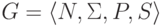 будем называть последовательность правил,
примененных в этом выводе.
Формально говоря,
протоколом левостороннего вывода
будем называть последовательность правил,
примененных в этом выводе.
Формально говоря,
протоколом левостороннего вывода
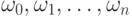
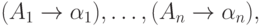
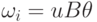 и
и  для некоторых
для некоторых 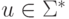 ,
, 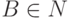 ,
, 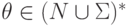 ,
, 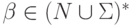 ,
то Ai+1 = B
и
,
то Ai+1 = B
и 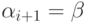 .
.Пример 13.1.3. Рассмотрим контекстно-свободную грамматику
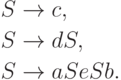
![\xymatrix @=6pt {
& & & & S\ar[ddllll]\ar[ddll]\ar[dd]\ar[ddrr]\ar[ddrrrr] \\
\\
a & & S\ar[dd] & & e & & S\ar[ddl]\ar[ddr] & & b \\
\\
& & c & & & d & & S\ar[dd] \\
\\
& & & & & & & c
}](/sites/default/files/tex_cache/cb4985ced830d8fbadae5d6e430cbbf8.png)
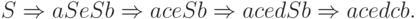
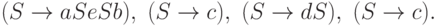
Лемма 13.1.4. Разным левосторонним выводам в одной и той же контекстно-свободной грамматике соответствуют разные протоколы.
Замечание 13.1.5. Протокол левостороннего вывода в контекстно-свободной грамматике является естественным описанием соответствующего дерева вывода в порядке префиксного обхода (preorder traversal). (При префиксном обходе упорядоченного дерева первым посещается корень этого дерева, затем выполняется префиксный обход первого непосредственного потомка корня, затем второго и т. д.)
Например, протокол левостороннего вывода из примера 13.1.3 задает процесс постепенного конструирования дерева вывода, изображенный ниже.
![\newcommand{\rb}[1]{\raisebox{0pt}[8pt]{$#1$}}
\entrymodifiers={=<3.3mm>[o]}
\xymatrix@=0mm{
&&&&&\boldsymbol{S}
\\
\\
\\
\\
&&&&&S\ar[ddddddlllll]<-1mm>\ar[ddl]\ar[ddddddl]\ar[ddr]\ar[ddddddrrrrr]<1mm>\\
\\
&&&&\boldsymbol{S}&&\boldsymbol{S}\\
\\
\\
\\
\rb{a}&&&&\rb{\boldsymbol{e}}&&&&&&\rb{\boldsymbol{b}}
\\
\\
&&&&&S\ar[ddddddlllll]<-1mm>\ar[ddl]\ar[ddddddl]\ar[ddr]\ar[ddddddrrrrr]<1mm>\\
\\
&&&&S\ar[ddddll]&&\boldsymbol{S}\\
\\
\\
\\
\rb{a}&&\rb{c}&&\rb{e}&&&&&&\rb{\boldsymbol{b}}
\\
\\
&&&&&S\ar[ddddddlllll]<-1mm>\ar[ddl]\ar[ddddddl]\ar[ddr]\ar[ddddddrrrrr]<1mm>\\
\\
&&&&S\ar[ddddll]&&S\ar[dddd]\ar[ddr]\\
\\
&&&&&&&\boldsymbol{S}\\
\\
\rb{a}&&\rb{c}&&\rb{e}&&\rb{d}&&&&\rb{\boldsymbol{b}}
\\
\\
&&&&&S\ar[ddddddlllll]<-1mm>\ar[ddl]\ar[ddddddl]\ar[ddr]\ar[ddddddrrrrr]<1mm>\\
\\
&&&&S\ar[ddddll]&&S\ar[dddd]\ar[ddr]\\
\\
&&&&&&&S\ar[ddr]\\
\\
\rb{a}&&\rb{c}&&\rb{e}&&\rb{d}&&\rb{c}&&\rb{b}
}](/sites/default/files/tex_cache/1456bb018af76b67230a0a44aa4b310e.png)
Определение 13.1.6. Левым разбором (left parse) слова w в контекстно-свободной грамматике G называется протокол любого левостороннего вывода слова w в грамматике G.
Пример 13.1.7. Левым разбором слова
aceaacecbecbb
в грамматике из примера 13.1.3 является последовательность
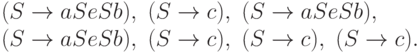
Определение 13.1.8. Процесс нахождения левого разбора слова w в заданной контекстно-свободной грамматике G называется нисходящим разбором (top-down parsing).
Определение 13.1.9. Вычислительным процессом МП-автомата M будем называть конечную последовательность его конфигураций, каждая из которых (кроме первой) получается из предыдущей одним тактом работы автомата M.
Пример 13.1.10. Рассмотрим МП-автомат
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix @=11mm{
*=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\rloop{0,1} ^{ab,\varepsilon:E}
\rloop{0,-1} ^{aa,E:\varepsilon}
\ar "1,2" <0.6mm> ^{b,\varepsilon:D}
& *=[o][F=]{2}
\ar "1,1" <0.6mm> ^{a,\varepsilon:D}
\rloop{0,1} ^{\varepsilon,D:\varepsilon}
\rloop{0,-1} ^{b,E:\varepsilon}
}](/sites/default/files/tex_cache/e69036021e3ea3c488962160adcc730f.png)

Определение 13.1.11.
Если в некотором вычислительном процессе
МП-автомата 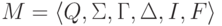 первая конфигурация имеет вид
первая конфигурация имеет вид 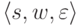 ,
где
,
где  и
и 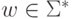 ,
а последняя конфигурация имеет вид
,
а последняя конфигурация имеет вид  ,
где
,
где  ,
то
будем говорить, что
этот вычислительный процесс допускает
слово w.
,
то
будем говорить, что
этот вычислительный процесс допускает
слово w.
Пример 13.1.12. Вычислительный процесс из примера 13.1.10 допускает слово bab.
Замечание 13.1.13.
МП-автомат M
допускает слово 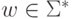 тогда и только тогда, когда
некоторый вычислительный процесс
МП-автомата M
допускает слово w.
тогда и только тогда, когда
некоторый вычислительный процесс
МП-автомата M
допускает слово w.
