|
Упражнение 2.1.25 |
Дополнительные свойства автоматных языков
Эта лекция содержит дополнительные результаты, не используемые в дальнейшем изложении. В начале лекции доказывается замкнутость класса всех автоматных языков относительно взятия гомоморфного образа и относительно взятия полного гомоморфного прообраза.
В разделе 4.2* определяются понятия побуквенного гомоморфизма и локального языка и доказывается еще один критерий автоматности: среди языков, не содержащих пустого слова, автоматными являются в точности образы локальных языков при побуквенных гомоморфизмах.
В последнем разделе этой лекции устанавливается числовой критерий автоматности для языков над однобуквенным алфавитом (в терминах арифметических прогрессий) и доказывается связанное с длинами слов необходимое условие автоматности (для произвольного алфавита).
4.1. Гомоморфизмы и автоматные языки
Теорема 4.1.1. Для любого гомоморфизма  и автоматного языка
и автоматного языка 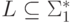 язык h(L) является автоматным.
язык h(L) является автоматным.
Доказательство.
Пусть исходный язык L
задан конечным автоматом 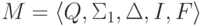 .
Положим
.
Положим
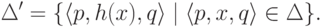
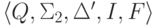 .
.Теорема 4.1.2. Для любого гомоморфизма  и автоматного языка
и автоматного языка  язык h-1(L) является автоматным.
язык h-1(L) является автоматным.
Доказательство.
Без ограничения общности можно предположить,
что исходный язык L
задан конечным автоматом 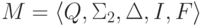 ,
где
,
где  не содержит переходов с метками длины больше единицы.
Положим
не содержит переходов с метками длины больше единицы.
Положим

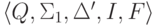 .
.Упражнение 4.1.3. Существует ли такой
автоматный язык L
над алфавитом {a,b},
что язык  не является автоматным?}
не является автоматным?}
Упражнение 4.1.4. Существует ли такой
автоматный язык L
над алфавитом {a,b},
что язык 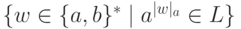 не является автоматным?}
не является автоматным?}
Упражнение 4.1.5. Существует ли такой
автоматный язык L
над алфавитом {a,b},
что язык  не является автоматным?
не является автоматным?

