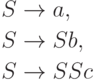|
Упражнение 2.1.25 |
Синтаксический разбор
Пример 13.1.29. Рассмотрим контекстно-свободную грамматику из примера 13.1.3. Грамматика с маркером конца строки имеет правила
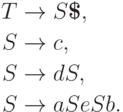
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix @=11mm{
*=[o][F-]{a}
\ar "2,3" <0.6mm> ^{\varepsilon,a:\varepsilon}
\rloop{-1,0} ^{\varepsilon,T:S\boldsymbol{\$}}
\rloop{0,1} ^{\varepsilon,S:aSeSb}
&
& *=[o][F-]{b}
\ar "2,3" <0.6mm> ^{\varepsilon,b:\varepsilon}
&
& *=[o][F-]{c}
\ar "2,3" <0.6mm> ^{\varepsilon,c:\varepsilon}
\rloop{1,0} ^{\varepsilon,T:S\boldsymbol{\$}}
\rloop{0,1} ^{\varepsilon,S:c}
\\
*=[o][F-]{q_{\textrm{s}}}
\ar @`{+/l16mm/} [] ^{}
\ar "2,3" ^{\varepsilon,\varepsilon:T}
&
& *=[o][F=]{\varepsilon}
\ar "1,1" <0.6mm> ^{a,\varepsilon:\varepsilon}
\ar "1,3" <0.6mm> ^{b,\varepsilon:\varepsilon}
\ar "1,5" <0.6mm> ^{c,\varepsilon:\varepsilon}
\ar "3,5" <0.6mm> ^{d,\varepsilon:\varepsilon}
\ar "3,3" <0.6mm> ^{e,\varepsilon:\varepsilon}
\ar "3,1" <0.6mm> ^{\boldsymbol{\$},\varepsilon:\varepsilon}
&
&
\\
*=[o][F-]{\boldsymbol{\$}}
\ar "2,3" <0.6mm> ^{\varepsilon,\boldsymbol{\$}:\varepsilon}
&
& *=[o][F-]{e}
\ar "2,3" <0.6mm> ^{\varepsilon,e:\varepsilon}
&
& *=[o][F-]{d}
\ar "2,3" <0.6mm> ^{\varepsilon,d:\varepsilon}
\rloop{1,0} ^{\varepsilon,T:S\boldsymbol{\$}}
\rloop{0,-1} ^{\varepsilon,S:dS}
}](/sites/default/files/tex_cache/541dcb79332ade51b77902d93f464b36.png)
Определение 13.1.30.
Контекстно-свободная грамматика 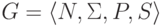 принадлежит классу LL(1),
если для любых двух правил
принадлежит классу LL(1),
если для любых двух правил  и
и  ,
где
,
где  ,
множества
,
множества  и
и 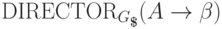 не пересекаются.
не пересекаются.
Замечание 13.1.31. Первая буква L в названии класса LL(1) означает, что входное слово читается слева направо (left-to-right). Вторая буква L означает, что строится левосторонний вывод (leftmost derivation). Число 1 указывает на то, что на каждом шаге для принятия решения используется один символ неразобранной части входного слова.
Пример 13.1.32. Грамматика из примера 13.1.3 принадлежит классу LL(1), а грамматика из примера 3.1.17 этому классу не принадлежит.
Теорема 13.1.33. МП-автомат M, построенный в теореме 13.1.28 по контекстно-свободной грамматике G, является детерминированным тогда и только тогда, когда грамматика G принадлежит классу LL(1).
Теорема 13.1.34. Грамматики из класса LL(1) порождают только детерминированные контекстно-свободные языки.
Теорема 13.1.35. Пусть
контекстно-свободная грамматика 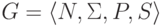 не содержит бесполезных символов.
Система множеств
не содержит бесполезных символов.
Система множеств  (где
(где  ) состоит из наименьших ( по включению ) множеств,
удовлетворяющих следующим условиям:
) состоит из наименьших ( по включению ) множеств,
удовлетворяющих следующим условиям:
-
если
 , то
, то 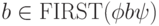 для всех
для всех  и
и  ;
; -
если
 , то
, то  для всех
для всех  и
и  ;
; -
если
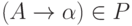 , то
, то  .
.
Теорема 13.1.36. Пусть
контекстно-свободная грамматика 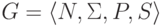 не содержит бесполезных символов.
Система множеств
не содержит бесполезных символов.
Система множеств  ( где
( где  ) состоит из наименьших ( по включению ) множеств,
удовлетворяющих следующим условиям:
) состоит из наименьших ( по включению ) множеств,
удовлетворяющих следующим условиям:
-
если
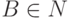 и
и  , то
, то  ;
; -
если
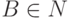 ,
,  и
и  , то
, то
Замечание 13.1.37. Теоремы 13.1.35 и 13.1.36 дают алгоритм проверки принадлежности контекстно-свободной грамматики G классу LL(1). Можно предположить, что грамматика G не содержит бесполезных символов (их можно устранить).
Сначала необходимо вычислить значения  параллельно для всех слов
параллельно для всех слов 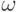 ,
являющихся суффиксами правых частей правил грамматики
,
являющихся суффиксами правых частей правил грамматики 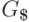 .
Для этого постепенно пополняем множества
.
Для этого постепенно пополняем множества  (начав с пустых множеств),
используя условия, приведенные в теореме 13.1.35.
(начав с пустых множеств),
используя условия, приведенные в теореме 13.1.35.
Затем необходимо вычислить значения  параллельно для всех
вспомогательных символов A.
Для этого постепенно пополняем множества
параллельно для всех
вспомогательных символов A.
Для этого постепенно пополняем множества  (начав с пустых множеств),
используя условия, приведенные в теореме 13.1.35.
(начав с пустых множеств),
используя условия, приведенные в теореме 13.1.35.
В заключение вычислим значения  для всех правил
для всех правил  ,
следуя определению функции
,
следуя определению функции  ,
и проверим условия из определения 13.1.30.
,
и проверим условия из определения 13.1.30.
Теорема 13.1.38.
Пусть даны
контекстно-свободная грамматика 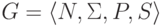 и символ
и символ  .
Пусть
.
Пусть

 не начинается с символа A.
Тогда грамматика G
эквивалентна
контекстно-свободной грамматике
не начинается с символа A.
Тогда грамматика G
эквивалентна
контекстно-свободной грамматике  ,
где A' -
новый символ, не принадлежащий множеству
,
где A' -
новый символ, не принадлежащий множеству  ,
и
,
и
Пример 13.1.39.
Если к контекстно-свободной грамматике 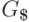 из примера 13.1.17
два раза применить преобразование из теоремы 13.1.38
(для вспомогательного символа A
и для вспомогательного символа B ),
то получим
эквивалентную грамматику G'
с правилами
из примера 13.1.17
два раза применить преобразование из теоремы 13.1.38
(для вспомогательного символа A
и для вспомогательного символа B ),
то получим
эквивалентную грамматику G'
с правилами


 ,
где
,
где  ,
, 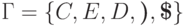 ,
,  ,
,  и
и

Пример 13.1.40.
Пусть  и
и 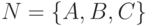 .
Рассмотрим контекстно-свободную
грамматику G
с правилами
.
Рассмотрим контекстно-свободную
грамматику G
с правилами


![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix @=11mm{
*=[o][F-]{\boldsymbol{m}}
\ar "2,3" <0.6mm> ^{\varepsilon,\boldsymbol{m}:\varepsilon}
\rloop{0,-1} ^{\varepsilon,T:A\boldsymbol{\$}}
\rloop{-1,0} ^{\varepsilon,A:CDE}
\rloop{0,1} ^{\varepsilon,C:\boldsymbol{m}}
&
& *=[o][F-]{q_{\textrm{s}}}
\ar @`{+/l16mm/} [] ^{}
\ar "2,3" ^{\varepsilon,\varepsilon:T}
&
& *=[o][F-]{\boldsymbol{\$}}
\ar "2,3" <0.6mm> ^{\varepsilon,\boldsymbol{\$}:\varepsilon}
\rloop{1,0} ^{\varepsilon,D:\varepsilon}
\rloop{0,-1} ^{\varepsilon,E:\varepsilon}
\\
%
&
& *=[o][F=]{\varepsilon}
\ar "1,1" <0.6mm> ^{\boldsymbol{m},\varepsilon:\varepsilon}
\ar "3,1" <0.6mm> ^{\boldsymbol{n},\varepsilon:\varepsilon}
\ar "3,3" <0.6mm> ^{\boldsymbol{*},\varepsilon:\varepsilon}
\ar "3,5" <0.6mm> ^{\boldsymbol{-},\varepsilon:\varepsilon}
\ar "1,5" <0.6mm> ^{\boldsymbol{\$},\varepsilon:\varepsilon}
&
&
\\
*=[o][F-]{\boldsymbol{n}}
\ar "2,3" <0.6mm> ^{\varepsilon,\boldsymbol{n}:\varepsilon}
\rloop{0,-1} ^{\varepsilon,T:A\boldsymbol{\$}}
\rloop{-1,0} ^{\varepsilon,A:CDE}
\rloop{0,1} ^{\varepsilon,C:\boldsymbol{n}}
&
& *=[o][F-]{\boldsymbol{*}}
\ar "2,3" <0.6mm> ^{\varepsilon,\boldsymbol{*}:\varepsilon}
\rloop{0,-1} ^{\varepsilon,D:\boldsymbol{*}CD}
&
& *=[o][F-]{\boldsymbol{-}}
\ar "2,3" <0.6mm> ^{\varepsilon,\boldsymbol{-}:\varepsilon}
\rloop{1,0} ^{\varepsilon,D:\varepsilon}
\rloop{0,-1} ^{\varepsilon,E:\boldsymbol{-}CDE}
}](/sites/default/files/tex_cache/0fba10db6bf9c19bc0e7c26b3d3c6d94.png)
Упражнение 13.1.41. Существует ли детерминированный нисходящий магазинный анализатор для грамматики

Упражнение 13.1.42. Принадлежит ли грамматика

Упражнение 13.1.43. Принадлежит ли грамматика