|
Упражнение 2.1.25 |
Слова, языки и грамматики
1.5. Классы грамматик
Определение 1.5.1. Контекстной грамматикой
(контекстно-зависимой грамматикой,
грамматикой непосредственно составляющих, НС-грамматикой,
грамматикой типа 1,
context-sensitive grammar,
phrase-structure grammar)
называется порождающая грамматика, каждое правило которой имеет вид  ,
где
,
где 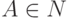 ,
, 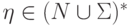 ,
, 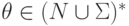 ,
, 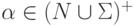 .
.
Пример 1.5.2. Грамматика

Определение 1.5.3. Контекстно-свободной грамматикой
( бесконтекстной грамматикой, КС-грамматикой,
грамматикой типа 2,
context-free grammar)
называется порождающая грамматика, каждое правило которой имеет вид  ,
где
,
где 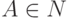 ,
, 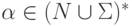 .
.
Пример 1.5.4. Грамматика
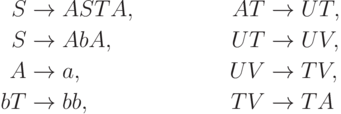
Определение 1.5.5. Линейной грамматикой
(linear grammar)
называется порождающая грамматика, каждое правило которой имеет вид  или
или 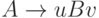 ,
где
,
где 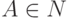 ,
, 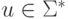 ,
,  ,
, 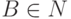 .
.
Грамматика

Определение 1.5.7. Праволинейной грамматикой
( рациональной грамматикой, грамматикой типа 3,
right-linear grammar)
называется порождающая грамматика, каждое правило которой имеет вид  или
или  ,
где
,
где 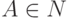 ,
, 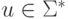 ,
, 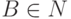 .
.
Пример 1.5.8. Грамматика
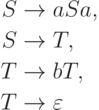
Пример 1.5.9. Грамматика
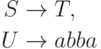
 .
.Пример 1.5.10. Грамматика
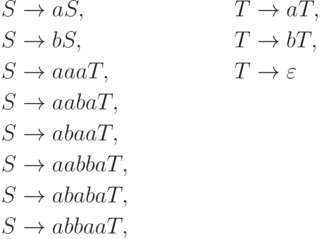
Пример 1.5.11. Грамматика
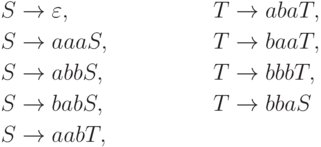
Определение 1.5.12.
Правила вида 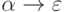 называются
называются  - правилами
или эпсилон-правилами.
- правилами
или эпсилон-правилами.
Лемма 1.5.13. Каждая праволинейная грамматика является линейной.
Каждая линейная грамматика является контекстно-свободной.
Каждая контекстно-свободная грамматика без  -правил
является контекстной грамматикой.
-правил
является контекстной грамматикой.
Определение 1.5.14. Классы грамматик типа 0, 1, 2 и 3 образуют иерархию Хомского (Chomsky hierarchy).
Определение 1.5.15. Язык называется языком типа 0 ( контекстным языком, контекстно-свободным языком, линейным языком, праволинейным языком ), если он порождается некоторой грамматикой типа 0 (соответственно контекстной грамматикой, контекстно-свободной грамматикой, линейной грамматикой, праволинейной грамматикой). Контекстно-свободные языки называются также алгебраическими языками.
Пример 1.5.16. Пусть дан произвольный алфавит
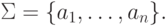
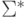 является праволинейным, так как он порождается грамматикой
является праволинейным, так как он порождается грамматикой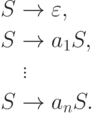
Упражнение 1.5.17. Какому классу принадлежит грамматика
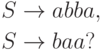
Упражнение 1.5.18. Какому классу принадлежит грамматика

Упражнение 1.5.19. Найти праволинейную грамматику, порождающую язык 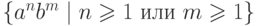 .
.
Упражнение 1.5.20. Найти праволинейную грамматику, эквивалентную грамматике
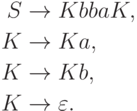
Упражнение 1.5.21. Найти праволинейную грамматику, эквивалентную грамматике

