| Россия, Новосибирск |
Теории и модели
Теорема 62. Пусть  — бесконечная нормальная интерпретация
сигнатуры
— бесконечная нормальная интерпретация
сигнатуры  (с равенством) и пусть
(с равенством) и пусть  —
мощность, не меньшая мощностей сигнатуры
—
мощность, не меньшая мощностей сигнатуры  и
интерпретации
и
интерпретации  . Тогда существует нормальное
элементарное расширение
. Тогда существует нормальное
элементарное расширение 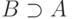 мощности
мощности  .
.
Мощность сигнатуры 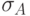 есть максимум из мощностей
есть максимум из мощностей  и
и  ; после добавления новых констант в
количестве
; после добавления новых констант в
количестве  штук получится сигнатура мощности
штук получится сигнатура мощности  , и согласно теореме 48 найдется модель
множества
, и согласно теореме 48 найдется модель
множества  мощности
мощности  . Преобразование ее
в нормальную модель (факторизация) может лишь уменьшить мощность,
но
. Преобразование ее
в нормальную модель (факторизация) может лишь уменьшить мощность,
но  различных элементов у нас заведомо есть.
различных элементов у нас заведомо есть.
Аналогичный прием (добавление констант) позволяет легко доказать такое утверждение:
Теорема 63. Если теория (в произвольной сигнатуре с равенством) имеет сколь угодно большие конечные нормальные модели, то она имеет и бесконечную нормальную модель.
Добавим к теории бесконечное число новых констант и аксиомы о том, что все они различны. Любой конечный фрагмент расширенной теории имеет нормальную модель (возьмем достаточно большую конечную модель и проинтерпретируем в ней константы). По теорме компактности и вся расширенная теория имеет нормальную модель, которая и будет бесконечной нормальной моделью исходной теории.
Вообще можно задать себе такой естественный вопрос. Пусть есть некоторая теория (или даже просто одна формула). Каковы могут быть мощности ее нормальных моделей? Как мы видели, для теорий с конечной сигнатурой верно одно из двух: либо бесконечных моделей вовсе нет, либо есть бесконечные модели всех мощностей. Это гарантируют теоремы Левенгейма-Сколема об элементарной подмодели (теорема 42) и о повышении мощности (теорема 61).
Что можно сказать про мощности конечных моделей? Для каждой формулы рассмотрим множество всех возможных мощностей ее конечных моделей. Его иногда называют спектром формулы. Это множество может быть устроено довольно сложным образом: например, для формулы, выражающей аксиомы поля, спектр состоит из всех степеней простых чисел.
116. (а) Укажите формулу, спектр которой состоит из всех четных положительных чисел. (б) Укажите формулу, спектр которой состоит из всех нечетных чисел. (в) Укажите формулу, спектр которой состоит из всех составных чисел.
Любопытно, что проблема конечного спектра
(приведенная в книге Кейслера и Чэна под номером 1 среди "старых проблем
теории моделей"), неожиданно оказалась связана с центральной
проблемой теории сложности вычислений — так называемой
"проблемой перебора". (Проблема конечного спектра состоит в
следующем: верно ли, что дополнение (до 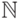 ) к спектру
любой формулы является спектром некоторой другой формулы?)
) к спектру
любой формулы является спектром некоторой другой формулы?)
В качестве примера использования теоремы о повышении мощности
докажем теорему Гильберта о нулях (теорема 40), не проводя
элиминацию кванторов. Пусть система уравнений имеет решение в поле 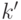 ,
являющемся расширением алгебраически замкнутого поля
,
являющемся расширением алгебраически замкнутого поля  .
Покажем, что она имеет решение и в
.
Покажем, что она имеет решение и в  . Построим элементарное
расширение
. Построим элементарное
расширение 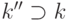 очень большой мощности. Теперь
очень большой мощности. Теперь 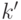 можно вложить в
можно вложить в  (это вложение строится по трансфинитной
рекурсии: добавляя алгебраический элемент, мы пользуемся
алгебраической замкнутостью
(это вложение строится по трансфинитной
рекурсии: добавляя алгебраический элемент, мы пользуемся
алгебраической замкнутостью  , добавляя трансцендентный
элемент, мы пользуемся большой мощностью
, добавляя трансцендентный
элемент, мы пользуемся большой мощностью  ). Значит, система
имеет решение в
). Значит, система
имеет решение в  . Поскольку
. Поскольку  было элементарным
расширением, то система имеет решение в
было элементарным
расширением, то система имеет решение в  .
.
Другое любопытное применение теоремы о повышении мощности
таково. Назовем линейно упорядоченное множество  однородным, если для любых двух возрастающих
последовательностей
однородным, если для любых двух возрастающих
последовательностей 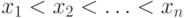 и
и 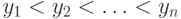 найдется автоморфизм
множества
найдется автоморфизм
множества  , переводящий
, переводящий  в
в  (при
всех
(при
всех 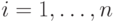 ).
).
Теорема 64. Для всякой бесконечной мощности найдется однородное линейно упорядоченное множество такой мощности.
Множество рациональных чисел (и вообще любое счетное плотное линейно упорядоченное множество) однородно. В самом деле, соответствие между двумя наборами его элементов постепенно продолжается до автоморфизма (добавляем элементы поочередно с той или другой стороны). Другой способ убедиться в этом — вспомнить о том, что это рациональные числа, и взять кусочно-линейный автоморфизм.
Для каждого  фиксируем способ продолжения автоморфизмов с
фиксируем способ продолжения автоморфизмов с  -элементных подмножеств в виде функции
-элементных подмножеств в виде функции 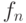 с
с 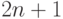 аргументами:
аргументами: 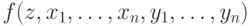 означает
элемент, в который переходит
означает
элемент, в который переходит  при автоморфизме, переводящем
при автоморфизме, переводящем  в
в  . Рассмотрим теперь
. Рассмотрим теперь  как интерпретацию сигнатуры, включающей порядок и все
как интерпретацию сигнатуры, включающей порядок и все  . По теореме о
повышении мощности можно найти элементарно эквивалентную
интерпретацию любой заданной мощности. Поскольку свойства
функций
. По теореме о
повышении мощности можно найти элементарно эквивалентную
интерпретацию любой заданной мощности. Поскольку свойства
функций 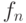 выражаеются формулами, получится однородное
линейно упорядоченное множество заданной мощности.
выражаеются формулами, получится однородное
линейно упорядоченное множество заданной мощности.
