| Россия, Новосибирск |
Арифметика Пресбургера
Теорема Тарского-Зайденберга
В этом разделе мы покажем, что в элементарной теории
действительных чисел со сложением и умножением
выполнима элиминация кванторов. Более точно, рассмотрим сигнатуру, содержащую
предикаты  и
и  , константы
, константы  и
и  , а также операции сложения и умножения. Рассмотрим интерпретацию этой сигнатуры,
носителем которой является множество действительных чисел, а
предикаты и операции понимаются естественным образом. Тогда для
каждой формулы существует эквивалентная (выражающая тот же
предикат) бескванторная формула. Это утверждение называют
теоремой Тарского-Зайденберга.
, а также операции сложения и умножения. Рассмотрим интерпретацию этой сигнатуры,
носителем которой является множество действительных чисел, а
предикаты и операции понимаются естественным образом. Тогда для
каждой формулы существует эквивалентная (выражающая тот же
предикат) бескванторная формула. Это утверждение называют
теоремой Тарского-Зайденберга.
Прежде чем доказывать эту теорему, сделаем несколько комментариев:
- Свойство
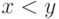 можно выразить как "существует ненулевое
можно выразить как "существует ненулевое  ,
для которого
,
для которого 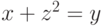 ". Таким образом, класс выразимых
предикатов не изменится, если мы удалим символ
". Таким образом, класс выразимых
предикатов не изменится, если мы удалим символ  из сигнатуры.
(Но предикатов, выразимых бескванторными формулами, станет
меньше: свойство
из сигнатуры.
(Но предикатов, выразимых бескванторными формулами, станет
меньше: свойство  , как легко понять, не эквивалентно
никакой бескванторной формуле, содержащей константы,
сложение, умножение и равенство.)
, как легко понять, не эквивалентно
никакой бескванторной формуле, содержащей константы,
сложение, умножение и равенство.) - Бескванторную формулу нашей сигнатуры можно привести к
дизъюнктивной нормальной форме, после чего она превратится в
совокупность систем уравнений вида
 и неравенств вида
и неравенств вида 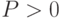 . В самом деле, в конъюнкциях могут еще быть отрицания, то
есть отношения
. В самом деле, в конъюнкциях могут еще быть отрицания, то
есть отношения 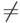 и
и  , но можно разбить
, но можно разбить 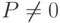 на
на 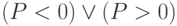 , а
, а  на
на 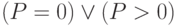 , после чего воспользоваться дистрибутивностью.
, после чего воспользоваться дистрибутивностью. - Подмножества
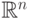 ,
задаваемые уравнениями вида
,
задаваемые уравнениями вида  и неравенствами
вида
и неравенствами
вида 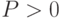 (где
(где  — произвольный многочлен от
нескольких переменных с целыми коэффициентами), а также множества,
получаемые из них любым числом операций объединения и
пересечения, называют полуалгебраическими.
Предыдущее замечание показывает, что всякая бескванторная формула задает
полуалгебраическое множество. (Полуалгебраические множества
являются обобщениями алгебраических множеств, задаваемых системами полиномиальных уравнений.)
— произвольный многочлен от
нескольких переменных с целыми коэффициентами), а также множества,
получаемые из них любым числом операций объединения и
пересечения, называют полуалгебраическими.
Предыдущее замечание показывает, что всякая бескванторная формула задает
полуалгебраическое множество. (Полуалгебраические множества
являются обобщениями алгебраических множеств, задаваемых системами полиномиальных уравнений.) - Из теоремы Тарского-Зайденберга вытекает, что проекция
полуалгебраического множества
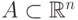 вдоль одной из
осей является полуалгебраическим подмножеством пространства
вдоль одной из
осей является полуалгебраическим подмножеством пространства 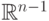 . В самом деле, переход к проекции приводит к
добавлению квантора существования, который можно затем
элиминировать. (Утверждение о полуалгебраичности проекции
полуалгебраического множества по существу равносильно теореме
Тарского-Зайденберга, так как элиминация квантора
существования является единственным нетривиальным шагом в
доказательстве этой теоремы.)
. В самом деле, переход к проекции приводит к
добавлению квантора существования, который можно затем
элиминировать. (Утверждение о полуалгебраичности проекции
полуалгебраического множества по существу равносильно теореме
Тарского-Зайденберга, так как элиминация квантора
существования является единственным нетривиальным шагом в
доказательстве этой теоремы.) - Пример: равенство
 задает полуалгебраическое (и даже
алгебраическое) множество троек
задает полуалгебраическое (и даже
алгебраическое) множество троек 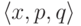 . Какова будет
его проекция вдоль оси
. Какова будет
его проекция вдоль оси  на плоскость
на плоскость 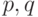 ? Как учат
в школе, это будет множество
? Как учат
в школе, это будет множество 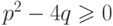 , которое оказывается
полуалгебраическим в полном согласии с теоремой Тарского-Зайденберга.
Про аналогичные критерии разрешимости уравнений большей степени в школе
не учат, но теорема Тарского-Зайденберга гарантирует их
существование.
, которое оказывается
полуалгебраическим в полном согласии с теоремой Тарского-Зайденберга.
Про аналогичные критерии разрешимости уравнений большей степени в школе
не учат, но теорема Тарского-Зайденберга гарантирует их
существование. - Как и во всех предыдущих случаях элиминации кванторов, преобразование формулы в бескванторную формулу эффективно (выполняется некоторым алгоритмом). В частности, этот алгоритм можно применить к замкнутой формуле (формуле без параметров). Тогда получится бескванторная формула без параметров (формально говоря, там могут быть параметры, от значений которых ничего не зависит, но их можно заменить, скажем, нулями). Истинность такой формулы можно алгоритмически проверить. Тем самым можно алгоритмически проверить истинность любого утверждения о действительных числах, выраженного формулой нашей сигнатуры. Как говорят, элементарная теория действительных чисел со сложением и умножением разрешима.
- Большинство утверждений школьного курса геометрии с помощью
метода координат можно записать как утверждения о действительных
числах в нашей сигнатуре. (Исключение, впрочем,
составляют утверждения, где речь идет не о треугольниках и четырехугольниках, а о
 -
угольниках без указания конкретного
-
угольниках без указания конкретного  ). Записав теоремы в
виде замкнутых формул нашей сигнатуры, можно алгоритмически
проверить их истинность. Тем самым мы получаем общий метод
доказательства большинства теорем школьной геометрии (впрочем,
он имеет лишь теоретическое значение, так как алгоритм работает
необозримо долго на сколько-нибудь сложных формулах).
). Записав теоремы в
виде замкнутых формул нашей сигнатуры, можно алгоритмически
проверить их истинность. Тем самым мы получаем общий метод
доказательства большинства теорем школьной геометрии (впрочем,
он имеет лишь теоретическое значение, так как алгоритм работает
необозримо долго на сколько-нибудь сложных формулах).
Теорема 33 (Тарского-Зайденберга). Для всякой формулы сигнатуры 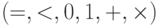 существует
бескванторная формула, задающая тот же предикат на множестве
действительных чисел.
существует
бескванторная формула, задающая тот же предикат на множестве
действительных чисел.
Как обычно, достаточно рассматривать формулу с единственным квантором
существования, то есть формулу  вида
вида
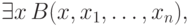
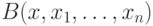 — бескванторная формула, включающая в
себя только переменные из числа
— бескванторная формула, включающая в
себя только переменные из числа  . Надо
доказать, что найдется эквивалентная формуле
. Надо
доказать, что найдется эквивалентная формуле  бескванторная формула
бескванторная формула 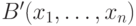 .
.Посмотрим на атомарные формулы, входящие в формулу  . Перенося
все переменные в одну часть, можно считать, что каждая атомарная
формула имеет вид
. Перенося
все переменные в одну часть, можно считать, что каждая атомарная
формула имеет вид 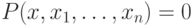 или
или 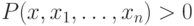 , где
, где  — некоторый многочлен
с целыми коэффициентами от переменных
— некоторый многочлен
с целыми коэффициентами от переменных  . Кольцо
многочленов с целыми коэффициентами от переменных
. Кольцо
многочленов с целыми коэффициентами от переменных  обозначается через
обозначается через ![\mathbb Z[x,x_1,\dots,x_n]](/sites/default/files/tex_cache/420eb44c65de5b2ba34dd8fdd1f0897e.png) .
Группировка членов по степеням переменной
.
Группировка членов по степеням переменной  дает многочлен от
дает многочлен от  , коэффициенты которого представляют собой многочлены от
, коэффициенты которого представляют собой многочлены от  . Символически это записывается так:
. Символически это записывается так:
![\mathbb Z[x,x_1,\dots,x_n]=(\mathbb Z[x_1,\dots,x_n])[x]](/sites/default/files/tex_cache/52c1acfe12e889686d84c285c8fe05f1.png)
 переменных можно рассматривать как
многочлены от одной переменной, коэффициенты которых лежат в
кольце многочленов от
переменных можно рассматривать как
многочлены от одной переменной, коэффициенты которых лежат в
кольце многочленов от  переменных).
переменных).При фиксации значений переменных  входящие в
входящие в  многочлены превращаются в многочлены от одной переменной
многочлены превращаются в многочлены от одной переменной  с
числовыми коэффициентами. Формула
с
числовыми коэффициентами. Формула  выражает тогда
какое-то свойство этих многочленов и может быть истинной или
ложной. Нам надо доказать, что те
выражает тогда
какое-то свойство этих многочленов и может быть истинной или
ложной. Нам надо доказать, что те 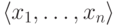 , при которых она истинна, образуют
полуалгебраическое множество.
, при которых она истинна, образуют
полуалгебраическое множество.
Для этого введем понятие диаграммы семейства многочленов.
Пусть 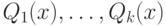 — многочлены от
— многочлены от  с действительными коэффициентами. Диаграммой набора
с действительными коэффициентами. Диаграммой набора 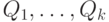 будет таблица, которая строится так. Возьмем все
корни всех многочленов
будет таблица, которая строится так. Возьмем все
корни всех многочленов 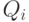 (не считая нулевых многочленов) и
расположим их в порядке возрастания. Получим некоторый набор
чисел
(не считая нулевых многочленов) и
расположим их в порядке возрастания. Получим некоторый набор
чисел  . Эти числа разбивают
числовую ось на
. Эти числа разбивают
числовую ось на 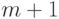 промежутков (два луча и
промежутков (два луча и 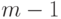 интервалов), на каждом из которых знаки всех
интервалов), на каждом из которых знаки всех 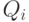 постоянны. Составим
таблицу, в которой будет
постоянны. Составим
таблицу, в которой будет  строк (по одной для каждого из
многочленов) и
строк (по одной для каждого из
многочленов) и 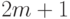 столбцов, соответствующих
столбцов, соответствующих  корням и
корням и 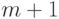 промежуткам (столбцы идут в порядке возрастания, так что
корни чередуются с промежутками). В каждой ячейке таблицы
запишем один из трех символов
промежуткам (столбцы идут в порядке возрастания, так что
корни чередуются с промежутками). В каждой ячейке таблицы
запишем один из трех символов 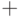 ,
,  или
или  в зависимости от
того, является ли многочлен положительным, отрицательным или
нулевым на соответствующем промежутке (или в соответствующем корне).
в зависимости от
того, является ли многочлен положительным, отрицательным или
нулевым на соответствующем промежутке (или в соответствующем корне).
