| Россия, Новосибирск |
Логика высказываний
Теорема 5 (о полиномах Жегалкина). Всякая булева функция однозначно представляется таким полиномом.
Существование искомого полинома следует из
теоремы 4, так как конъюнкция есть умножение, отрицание — прибавление единицы, а
дизъюнкцию можно через них выразить (получится 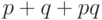 ). Надо
только заметить, что степени не нужны: переменные
принимают значения
). Надо
только заметить, что степени не нужны: переменные
принимают значения  и
и  , так что
, так что 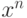 можно заменить на
можно заменить на 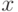 .
.
Можно также сослаться на известное из алгебры утверждение о том,
что всякая функция с аргументами из конечного поля (в данном
случае это двухэлементное поле вычетов по модулю 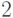 ) задается
полиномом. (Отсюда, кстати, получается новое доказательство
теоремы 3.)
) задается
полиномом. (Отсюда, кстати, получается новое доказательство
теоремы 3.)
Далее можно заметить, что полиномов столько же, сколько
булевых функций, а именно 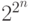 . В самом деле, булева
функция может принимать любое из двух значений в каждой из
. В самом деле, булева
функция может принимать любое из двух значений в каждой из 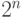 точек булева куба
точек булева куба 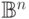 , а многочлен может
включать или не включать любой из
, а многочлен может
включать или не включать любой из 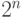 мономов. (Мономов
ровно
мономов. (Мономов
ровно 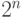 , потому что каждый моном включает или не включает любую из
, потому что каждый моном включает или не включает любую из 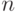 переменных.) Поэтому избытка полиномов нет, и если любая
функция представима полиномом, то единственным образом.
переменных.) Поэтому избытка полиномов нет, и если любая
функция представима полиномом, то единственным образом.
Можно и не ссылаться на сведения из алгебры и
теорему 4, а дать явную конструкцию. Это удобно сделать индукцией по 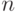 .
Пусть мы уже умеем представлять любую булеву функцию от
.
Пусть мы уже умеем представлять любую булеву функцию от 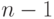 аргументов с
помощью полинома. Тогда
аргументов с
помощью полинома. Тогда 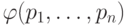 можно представить как
можно представить как
![\varphi(p_1,\dots,p_n) = \varphi(0, p_2,\dots,p_{n})+[\varphi(0,p_2,\dots,p_{n})+\varphi(1,p_2,\dots,p_{n})]p_1](/sites/default/files/tex_cache/ee4ab7336853520ec650d98d822a36eb.png)
Для единственности также есть другое доказательство: пусть два
многочлена (имеющие степень  по каждой переменной) равны при
всех значениях переменных. Тогда их сумма (или разность —
вычисления происходят по модулю
по каждой переменной) равны при
всех значениях переменных. Тогда их сумма (или разность —
вычисления происходят по модулю  ) является ненулевым
многочленом (содержит какие-то мономы), но тождественно равна
нулю. Так не бывает, и это легко доказать по индукции. В самом
деле, любой многочлен
) является ненулевым
многочленом (содержит какие-то мономы), но тождественно равна
нулю. Так не бывает, и это легко доказать по индукции. В самом
деле, любой многочлен 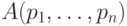 можно представить в
виде
можно представить в
виде
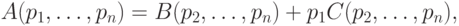
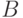 и
и 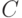 — многочлены от меньшего числа переменных.
Подставляя сначала
— многочлены от меньшего числа переменных.
Подставляя сначала 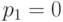 , а затем
, а затем 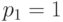 ,
убеждаемся, что многочлены
,
убеждаемся, что многочлены 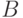 и
и 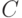 равны нулю во всех точках, и
потому (согласно предположению индукции) равны нулю как многочлены (не содержат мономов).
равны нулю во всех точках, и
потому (согласно предположению индукции) равны нулю как многочлены (не содержат мономов).11. Пусть 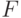 — произвольное поле.Назовем мультилинейной
функцией полином от
— произвольное поле.Назовем мультилинейной
функцией полином от 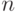 переменных с коэффициентами
из
переменных с коэффициентами
из 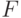 , в котором все показатели степеней равны либо
, в котором все показатели степеней равны либо  ,
либо
,
либо  . (Таким образом, каждый моном в ней есть произведение коэффициента и
некоторого набора переменных без повторений.) Будем
рассматривать
. (Таким образом, каждый моном в ней есть произведение коэффициента и
некоторого набора переменных без повторений.) Будем
рассматривать  как подмножество
как подмножество 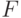 .
Докажите, что всякая булева функция
.
Докажите, что всякая булева функция  однозначно продолжается до
мультилинейной функции
однозначно продолжается до
мультилинейной функции 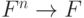 , и коэффициенты мультилинейной функции можно считать целыми числами.
, и коэффициенты мультилинейной функции можно считать целыми числами.
Если рассматривать произвольные булевы функции в качестве связок, возникает вопрос: в каком случае набор булевых функций образует полный базис? (Это значит, что любая булева функция представляется в виде композиции функций из набора, т. е. записывается в виде формулы, где связками служат функции набора.) Подобные вопросы вызывали в свое время большой интерес и были хорошо изучены. Начальным этапом явилось такое утверждение:
Теорема 6 (критерий Поста). Набор булевых функций является полным тогда и только тогда, когда он не содержится целиком ни в одном из пяти следующих "предполных классов":
- монотонные функции;
- функции, сохраняющие нуль;
- функции, сохраняющие единицу;
- линейные функции;
- самодвойственные функции.
(Функция  монотонна, если она монотонно неубывает по
каждому из своих аргументов. Функция
монотонна, если она монотонно неубывает по
каждому из своих аргументов. Функция  сохраняет
нуль/единицу, если
сохраняет
нуль/единицу, если 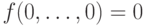 (соответственно
(соответственно 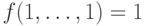 ). Функция
). Функция  линейна,
если она представима многочленом, в котором все мономы содержат не более
одной переменной. Наконец, функция
линейна,
если она представима многочленом, в котором все мономы содержат не более
одной переменной. Наконец, функция  называется
самодвойственной, если
называется
самодвойственной, если 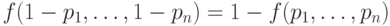 .)
.)
Если набор содержится в одном из классов, то и все композиции также не выходят за пределы этого класса (легко проверить для каждого из классов в отдельности) и поэтому набор не является полным. Докажем обратное утверждение. Пусть для каждого класса выбрана какая-то функция, в нем не лежащая. Убедимся, что с помощью комбинаций выбранных функций можно получить все булевы функции.
У нас есть функция, не сохраняющая нуль. Подставим вместо всех
аргументов одну и ту же переменную. Получится функция от одного
аргумента, отображающая нуль в единицу, то есть либо константа  , либо отрицание. Сделав то же самое с функцией, не
сохраняющей единицу, получим либо константу нуль, либо
отрицание. Таким образом, у нас либо есть отрицание, либо обе
константы
, либо отрицание. Сделав то же самое с функцией, не
сохраняющей единицу, получим либо константу нуль, либо
отрицание. Таким образом, у нас либо есть отрицание, либо обе
константы  и
и  .
.
Если есть обе константы, то все равно можно получить отрицание. Возьмем немонотонную функцию. Легко понять, что она должна менять значение с единицы на нуль при изменении какого-то одного аргумента с нуля на единицу (в самом деле, будем увеличивать аргументы по одному, в какой-то момент значение функции уменьшится.) Зафиксировав значения остальных аргументов (ведь мы считаем, что константы есть), получаем отрицание.
Имея отрицание и несамодвойственную функцию, легко получить
константы (если их не было). В самом деле, несамодвойственность
означает, что 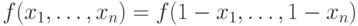 для каких-то значений
для каких-то значений 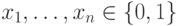 . Вместо
нулевых значений переменных
. Вместо
нулевых значений переменных  подставим
подставим 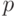 , вместо единиц подставим
, вместо единиц подставим 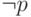 , получится одна из констант.
Вторая получится отрицанием.
, получится одна из констант.
Вторая получится отрицанием.
Теперь у нас есть константы, отрицание и нелинейная функция 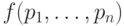 . Нелинейность означает, что в ее
представлении в виде многочлена есть моном, состоящий более чем из
одной переменной. Пусть, например, этот моном содержит переменные
. Нелинейность означает, что в ее
представлении в виде многочлена есть моном, состоящий более чем из
одной переменной. Пусть, например, этот моном содержит переменные  и
и 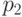 . Сгруппируем члены по четырем группам и получим выражение
. Сгруппируем члены по четырем группам и получим выражение
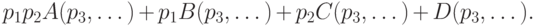
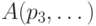 заведомо отличен от нуля, поэтому
можно так подставить константы вместо
заведомо отличен от нуля, поэтому
можно так подставить константы вместо 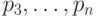 , чтобы
первое слагаемое не обратилось в нуль. Тогда получим либо
, чтобы
первое слагаемое не обратилось в нуль. Тогда получим либо 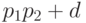 , либо
, либо 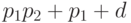 , либо
, либо 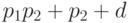 , либо
, либо 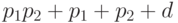 . Свободный член
. Свободный член 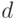 можно менять,
если нужно (у нас есть отрицание), так что получается либо
можно менять,
если нужно (у нас есть отрицание), так что получается либо 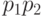 (конъюнкция, и все доказано), либо
(конъюнкция, и все доказано), либо 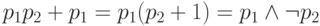 (убираем отрицание, получаем конъюнкцию, все
доказано), либо
(убираем отрицание, получаем конъюнкцию, все
доказано), либо 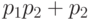 (аналогично), либо
(аналогично), либо 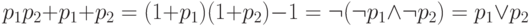 (дизъюнкция, все доказано).
(дизъюнкция, все доказано).