|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Эконометрический анализ инфляции
Нет необходимости связывать индекс инфляции с каким-либо определенным интервалом времени и даже с определенным социально-экономическим строем. Можно формально вычислить индексы инфляции и за весьма длительные промежутки времени. Так, например, рост цен на основные продукты питания с 1913 г. по апрель 1994 г. представлен в табл.7.5.
| Наименование продукта | Цена в 1913 г. (руб/ кг) | Цена в апр. 1994 г. (руб/кг) |
|---|---|---|
| Хлеб пшеничный | 0-05 | 740 |
| Хлеб ржаной | 0-03 | 400 |
| Молоко | 0-14 | 625 |
| Сыр | 0-40 | 6150 |
| Масло сливочное | 0-55 | 5100 |
| Масло растительное | 0-13 | 2300 |
| Сметана | 0-30 | 2500 |
| Говядина | 0-23 | 2760 |
| Свинина | 0-20 | 4000 |
| Баранина | 0-17 | 2000 |
Используя объемы потребления из потребительской корзины ИВСТЭ, получаем, что индекс инфляции за 1913-1994 гг. составил 1129600,6 %.
Результаты расчетов по различным потребительским корзинам дают, естественно, различные значения индексов инфляции, хотя эти различия, как представляется, не слишком значительны (табл.7.6). Близость различных индексов инфляции за большой промежуток времени объясняется тем, что цены растут в целом достаточно согласованно, "аномалии" выправляются: если темп роста цены определенного продукта отстает от среднего роста цен, то имеются основания полагать, что его цена в ближайшее время сильно возрастет. Однако на малых и средних промежутках времени проявляется различие роста цен на отдельные товары.
Тем более интересно, что официально публикуемые индексы инфляции Госкомстата РФ при отсчете с 1990 г. (или с 14.03.91) дают по крайней мере вдвое меньшие значения, чем расчеты Института высоких статистических технологий и эконометрики (подробнее см. коллективную монографию [3]).
| По нормам Госкомстата РФ | По нормам ИВСТЭ | |
|---|---|---|
|
с 14.03.91 по 14.03.94 |
30,82 / 48990,33 1589,8 |
26,85 / 40889,1 1598,88 |
|
с 15.11.93 по 14.03.94 |
31255 / 48990,33 1,57 |
28050 / 40889,1 1,46 |
|
с 19.05.94 по 26.05.94 |
56670,2 / 57667,75 1,02 |
55615 / 56332 1,01 |
Примечание. В табл.7.6 верхние числа - стоимости потребительских корзин соответственно на первую указанную дату и через дробь - на вторую, нижнее число - индекс инфляции за данный период.
Соотношение индексов инфляции для трех моментов времени. Рассмотрим три момента времени  и соответствующие индексы инфляции
и соответствующие индексы инфляции  и
и  . Из определения индекса инфляции как отношения стоимостей потребительской корзины в соответствующие моменты времени вытекает следующее утверждение.
. Из определения индекса инфляции как отношения стоимостей потребительской корзины в соответствующие моменты времени вытекает следующее утверждение.
Теорема 3 (теорема умножения). Для любых трех моментов времени  справедливо равенство
справедливо равенство 
Теорема умножения позволяет переходить от индексов инфляции за отдельные недели к индексам инфляции за месяц (четыре недели), от помесячных индексов инфляции - к квартальным и годовым, от годовых - к индексам инфляции за несколько лет. Например, индекс инфляции за второй квартал - с 01.04.94 по 01.07.94 - т.е. 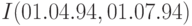 , выражается через индексы инфляции за апрель
, выражается через индексы инфляции за апрель 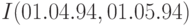 , май
, май  и июнь
и июнь 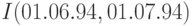 соответственно как произведение этих индексов, т.е. находится по формуле
соответственно как произведение этих индексов, т.е. находится по формуле

Аналогично индекс инфляции за год равен произведению двенадцати индексов инфляции: за январь, февраль, март и остальные девять месяцев.
В приведенных выше рассуждениях индекс инфляции рассматривался как положительное число, как говорят, выражался "в разах". Распространено его выражение "в процентах". Напомним, что индексы инфляции "в разах"  и "в процентах"
и "в процентах"  связаны соотношениями
связаны соотношениями

Таким образом, выражения "индекс инфляции за месяц составил 1,16" и "индекс инфляции за месяц составил 16%" означают одно и то же.
Поскольку для любых чисел 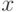 и
и 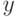 справедливо тождество
справедливо тождество

то, как легко проверить, для индексов инфляции "в процентах" справедливо тождество

Если индексы инфляции "в процентах" 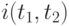 и
и  малы, т.е. индексы инфляции "в разах"
малы, т.е. индексы инфляции "в разах"  и
и  мало отличаются от единицы, то справедлива приближенная формула
мало отличаются от единицы, то справедлива приближенная формула 
Погрешность этой формулы, измеряемая в процентах, равна
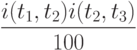
Эта величина становится заметной, если сомножители - порядка десятков (процентов). Если формула применяется несколько раз, то погрешность накапливается.
Рассмотрим пример. В известном учебнике экономической теории [4] рассмотрена связь между ежегодным увеличением цен и числом лет, необходимых для увеличения цен вдвое. Приведено правило, которое вначале выглядит совершенно непонятным: (приблизительное количество лет, необходимое для удвоения удвоение цен) = 70 / (темп ежегодного увеличения уровня цен в % ).
Действительно, пусть 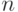 - количество лет, необходимое для удвоения цен, а
- количество лет, необходимое для удвоения цен, а 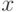 - темп ежегодного увеличения уровня цен (в % - 100x %). При "подходе профана" рост за
- темп ежегодного увеличения уровня цен (в % - 100x %). При "подходе профана" рост за 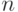 лет составит
лет составит  , а потому срок удвоения цен должен находиться из условия
, а потому срок удвоения цен должен находиться из условия  , т.е. в числителе дроби должно стоять число 100, а не 70. В чем дело?
, т.е. в числителе дроби должно стоять число 100, а не 70. В чем дело?
А дело в том, что рост описывается не линейной функцией, а экспоненциальной, надо не складывать, а возводить в степень. За 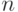 лет рост цен составит
лет рост цен составит 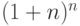 Период удвоения находится из уравнения
Период удвоения находится из уравнения

Тогда

Воспользуемся приближенной формулой математического анализа
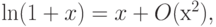
тогда с точностью до бесконечно малых более высокого порядка

Остается заметить, что

т.е. с достаточной для подобных расчетов точностью  .
.
Некоторые ошибки при расчетах с индексами инфляции. Информация об индексах инфляции и рассуждения, связанные с ними, постоянно появляются на страницах печати и обсуждаются в иных средствах массовой информации. К сожалению, достаточно распространены ошибки.
Так, в одной из экономических (!) газет была помещена публикация, в которой основной исходный материал для обсуждения - следующие индексы инфляции (по отношению к предыдущему месяцу):
январь - 1, февраль - 1,23, март - 1,19, апрель - 1,25,
май - 1,29, июнь - 1,3, июль - 1,23, август - 1,22,
сентябрь - 1,22, октябрь - 1,19, ноябрь - 1,23, декабрь - 1,25.
Автору публикации были нужны индексы инфляции за несколько месяцев. Рассчитывая их, он без каких-либо сомнений пользовался приближенной формулой предыдущего подпункта (сложение приращений в процентах) вместо точной (перемножение индексов инфляции, выраженных "в разах"). В результате он получил для периода январь-декабрь значение индекса инфляции  , в то время как на самом деле индекс инфляции, рассчитанный в результате перемножения индексов по месяцам, равен 10,23. Допущенная ошибка в
, в то время как на самом деле индекс инфляции, рассчитанный в результате перемножения индексов по месяцам, равен 10,23. Допущенная ошибка в 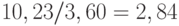 раза существенно исказила дальнейшие расчеты (фонда оплаты труда, средней зарплаты) в рассматриваемой публикации, названной в специализированной экономической газете не как-нибудь, а "консультацией" !
раза существенно исказила дальнейшие расчеты (фонда оплаты труда, средней зарплаты) в рассматриваемой публикации, названной в специализированной экономической газете не как-нибудь, а "консультацией" !
В еженедельнике "Аргументы и факты" в апреле 1994 г. в рубрике "Прогноз" помещена беседа журналистки Татьяны Коростиковой с первым заместителем министра экономики России Яковом Уринсоном [5], в которой Я. Уринсон прогнозирует:
"…Мы предполагаем рост цен за 1994 г. в 5 раз\dots В месяц- 7-8%\dots"
Сказанное противоречиво. Если индекс инфляции за год равен 5,0, то за месяц, очевидно, рост цен равен в среднем

т.е. 14,35% в месяц, а не 7-8%. Если же рост цен составляет 7-8% в месяц, то индекс инфляции за год лежит между  и
и  т.е. по крайней мере в два раза меньше, чем названный в беседе достаточно реальный прогноз - рост в 5 раз. Остается неясным, кто дезориентировал читателя многотиражного издания - чиновник или журналист. Наш запрос об этом в редакцию "Аргументов и фактов" остался без ответа.
т.е. по крайней мере в два раза меньше, чем названный в беседе достаточно реальный прогноз - рост в 5 раз. Остается неясным, кто дезориентировал читателя многотиражного издания - чиновник или журналист. Наш запрос об этом в редакцию "Аргументов и фактов" остался без ответа.
Приведенных примеров достаточно для констатации того, что к сообщениям в средствах массовой информации, посвященным росту цен, следует относиться с известной осторожностью.
