Финансовые ренты

6.4 Бессрочная рента

По количеству членов ренты делят на конечные или ограниченные по срокам и бесконечные или бессрочные, вечные. Бессрочная рента (далее мы будем использовать именно этот термин), или перпетуитет - это рента, выплаты которой не ограничены никаким сроком. Иначе говоря, число членов такой ренты бесконечно. Приведём пример бессрочной ренты. Некоторое благотворительное общество положило в банк определенную сумму денег и перечисляет ежегодно проценты, начисляемые на эту сумму, в пользу детского дома. Количество платежей, которые получит детский дом, ограничено только сроком существования банка, в котором размещены деньги. Следовательно, если пренебречь возможностью разорения банка, эти платежи образуют бессрочную ренту.

Обычно считается, что рента является бессрочной, если количество платежей её весьма велико и их прекращение не оговаривается конкретной датой. Как бессрочную ренту можно рассматривать выплату фиксированных купонных платежей по облигационным займам с большим сроком действия. Заметим, что выпуск вечных облигаций (или бондов) популярен и в наши дни у правительств разных стран. В феврале 2005 г. Франция разместила 50-летние облигации, спрос на которые в 3 раза превысил предложение. В этом же году Нидерланды разместили 30-летние облигации. А в феврале 2006 г. Минфин США выпустил 30-летние облигации на сумму 14 млрд, спрос на них более чем в 2 раза превысил предложение. В России впервые вечные облигации выпустил банк ВТБ (2012 г.). В этом же году Газпромбанк также выпустил вечные облигации.

Классификация бессрочных рент по способам начисления процентов и срокам выполнения платежей (обычные и авансированные) полностью совпадает с классификацией конечных рент. Для бессрочной ренты верны все приведенные в этой главе формулы, если применять эти формулы для определения наращенной суммы бессрочной ренты за n периодов. Не так будет обстоять дело при оценивании приведённой ценности ренты, которую мы будем рассматривать в следующей главе.

6.5 Вычисление платежей финансовой ренты

Из всех выведенных в этой лекции формул для вычисления наращенных сумм ренты S легко получить формулы для определения рентных платежей R. Приведем пример.

Формула (47) устанавливает зависимость между четырьмя величинами: R, n, i, S. Следовательно, фиксировав значения трех из этих величин, получаем уравнение для определения четвертой. В том случае, если известны значения n, i и S, а требуется определить величину платежа R, то из формулы (6.3) получаем равенство:

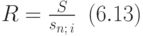
Рассмотрим пример на применение формулы (6.13).

Пример 59. Сын хочет накопить за 5 лет 500 000 руб. к юбилею матери, делая ежегодные равные вклады в банк, который выплачивает проценты по годовой ставке 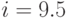(сложных). Какую сумму ему придется вкладывать каждый год?

Решение. По условию задачи имеем: S=500 000, n=5, i=0.095. Любым из предложенных ранее способов можно вычислить, что . По формуле (6.13) получаем:

Следовательно, в конце каждого года сын должен вкладывать в банк 82 718.20 руб.

6.6 Погашение долгосрочной задолженности единовременным платежом}

Рассмотрим следующую ситуацию. Должник взял ссуду, равную S~руб., которую он должен вернуть через n~лет одним платежом. Ежегодно до момента погашения ссуды он должен выплачивать кредитору проценты по ставке q. Одновременно с получением ссуды должник создает погасительный (амортизационный или страховой) фонд, в который делает в конце каждого года равные взносы с целью накопить к моменту возвращения долга сумму~S. На деньги, находящиеся в фонде, должник получает i% в год. Требуется определить, так называемую, срочную уплату , то есть суммарные ежегодные выплаты должника за использование ссуды.

Срочная уплата состоит из выплачиваемых за долг процентов, которые равны Sq, и взноса в страховой фонд, который мы обозначим через R. Взносы R образуют обычную годовую ренту, состоящую из n-членов, наращенная сумма которой в момент n должна быть равна S. По формуле (6.13) 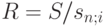. Следовательно, срочная уплата равна:

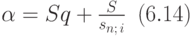
Рассмотрим пример на применение формулы (6.14).

Пример 60. Кредит в 1 млн руб. получен фирмой в банке под 13% годовых на 4 года. Одновременно с получением кредита для его погашения создан страховой фонд, в который делаются равные ежегодные взносы. На деньги, внесенные в фонд, выплачиваются 5% годовых. Найдем ежегодную срочную уплату по долгу.

Решение. По формуле (6.14) при S=1 000 000, q=0.13, n=4, i=0.05 находим величину срочной уплаты, предварительно вычислив, что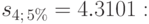

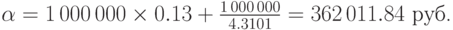
При других условиях начисления процентов страховым фондом будут возникать иные виды рент и потребуется использовать соотвествующие им формулы.

Погашение долгосрочной задолженности несколькими платежами будет рассмотрено в следующей лекции.